4 Классификация движений точки

Выясним зависимость характера движения точки от значений ее нормального и касательного ускорений.

С л у ч а й I: Если в течение некоторого промежутка времени нормальное и касательное ускорения точки равны нулю, то в течение этого промежутка не изменяются ни направление, ни модуль скорости, т. е. точка движется равномерно-прямолинейно и ее уско­рение .

С л у ч а й II: . Если в течение некоторого проме­жутка времени не равно нулю нормальное ускорение и равно нулю касательное ускорение, то происходит изменение направления скорости без изменения ее модуля, т. е. точка движется равномерно-криволинейно и модуль ее ускорения (рис. 9.8).

Рис. 9.8

Если в отдельный момент времени, то точка не движется равномерно, а в этот момент времени модуль ее скорости имеет максимум, минимум или наименьшую быстроту монотонного изменения.

С л у ч а й III: . Если в течение некоторого проме­жутка времени равно нулю нормальное ускорение точки и не равно нулю касательное, то не изменяется направление скорости, а изменя­ется ее модуль, т.е. точка движется по прямой неравномерно. Модуль ускорения точки в этом случае

Рис. 9.9

При этом если направления векторов и совпадают, то дви­жение точки ускоренное (рис. 9.9, а). Если направления векторов и противоположны, то движение точки замедленное (рис. 9.9, б). Если в некоторый момент времени, то точка не движется прямолинейно, а проходит точку перегиба траектории ( ) (рис. 9.9, в) или модуль ее скорости обращается в нуль (например, при изменении направления движения точки v=0).

С л у ч а й IV: . Если в течение некоторого проме­жутка времени ни нормальное, ни касательное ускорения точки не равны нулю, то изменяется как направление, так и модуль ее ско­рости, т. е. точка совершает неравномерно-криволинейное движение. Модуль ускорения точки

.

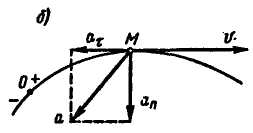
Рис. 9.10

При этом если направления векторов и , совпадают, то движе­ние ускоренное (рис. 9.10, а), а если они противоположны, то движение замедленное (рис. 10, б).

Если модуль касательного ускорения постоянен, т.е. , то модуль скорости точки изменяется пропорционально времени, т. е. точка совершает равнопеременное движение.

4. Равномерное и равнопеременное движение точки Равномерное движение точки

Равномерным движение будет в том случае, когда алгебраическое значение скорости остается неизменным. При этом траектория движения точки может быть любой формы.

Найдем закон равномерного движения точки. Известно, что

, так как ,

разделив переменные

и проинтегрировав левую и правую части равенства в пределах до и до соответственно, получим

или

. (9.14)

Выражение (9.14) называется уравнением равномерного движения точки. При . Данное утверждение справедливо как для прямолинейного ( ), так и для криволинейного движения ( ).

Изменение дуговой координаты ( ), скорости ( ) и касательного ускорения ( ) в течение времени можно показать графически (рис. 9.11).

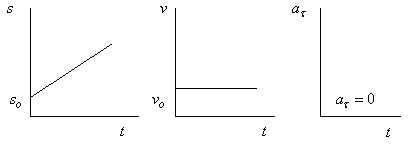
Рис. 9.11

График равномерного движения представляет собой прямую, направленную под углом к оси абсцисс, график скорости – прямая, параллельная оси абсцисс, график ускорения – прямая, совпадающая с осью абсцисс( рис. 9.11).