Раздел 2 Кинематика Лекция 8 кинематика точки

1 Предмет и задачи кинематики

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел. Движущиеся тала рассматриваются как чисто геометрические объекты - и тела – без учета их материальных характеристик (массы и др.). При этом не рассматриваются причины (действующие на тела силы), вызывающие и изменяющие движение объекта.

Под движением в механике понимается изменение с течением времени положения в пространстве данного тела по отношению к какому-либо другому телу. Характер наблюдаемого движения существенно зависит от выбора тела, с которым связан наблюдатель. С твердым телом, по отношению к которому изучается движение, жестко соединяют какую-нибудь систему координат, образующую вместе с этим телом систему отсчета. Пространство в механике рассматривается как трехмерное эвклидово. Время считается универсальным, т. е. протекающим одинаково во всех рассматриваемых системах отсчета. В задачах кинематики время (скалярная непрерывно изменяющаяся величина) принимается за независимое переменное (аргумент). Отсчет времени ведется от некоторого условного начального момента, о выборе которого в каждом случае условливаются. меняющаяся величина. За единицу времени принимается одна секунда, равная 1/(24*3600) средних солнечных суток.

Все кинематические величины, характеризующие движение твердого тела и движение отдельной его точки (расстояния, скорости, ускорения и т. д.), рассматриваются как функции времени.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано.

Кинематически задать движение тела (точки) – значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Если положение тела (точки) определяется какими-либо координатами (параметрами), то надо задать зависимость от времени t. Такая зависимость называется кинематическими уравнениями движения или законом движения.

Основной задачей кинематики является установления математических способов задания движения тела (точки) и методов определения всех кинематических величин, характеризующих данное движение.

Движение точки считается заданным, если указан способ, позволяющий определить положение точки в каждый момент времени относительно выбранной системы отсчета. Существует три способа задания движения точки: 1) векторный; 2) координатный; 3) естественный. Векторный способ применяется главным образом при исследовании теоретических вопросов, а координатный и естественный употребляются преимущественно при решении различных практических задач.

Теперь последовательно разберем эти три способа задания движения точки.

2 Способы задания движения точки Векторный способ задания движения точки

 

Положение точки в пространстве однозначно определяется заданием радиуса-вектора , проведенного из некоторого неподвижного центра О в данную точку М (рис. 8.1 ).

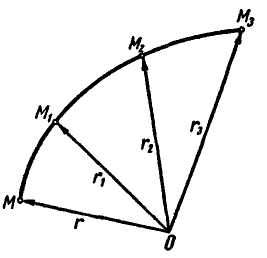
Рис. 8.1

Траектория точки является геомет­рическим местом концов радиуса-векто­ра движущейся точки.

Линия, образованная концами пере­менного вектора, начало которого нахо­дится в определенной точке пространства, называется годографом этого вектора.

Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор , т. е. должна быть задана вектор-функция аргумента t:

(8.1)

Следовательно, траектория точ­ки М является годографом ее радиуса-вектора .

Векторный способ определения дви­жения материальной точки или системы материальных точек широко использу­ется и в кинематике, и в динамике, так как он значительно упрощает многие выводы и иногда подчеркивает физическую сущность явлений. От векторных формул легко перейти к аналитическим выражениям, обычно более удобным для вычислений.

Координатный способ задания движения

Положение точки М в системе отсчета Охуz определяется тремя декартовыми координатами точки х, у, z (рис. 8.2). При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, у, z движущейся точки М являются функциями времени t:

. (8.2)

Эти уравнения называются уравнениями движения точки в декарто­вых координатах.

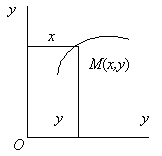
Рис. 8.2 Рис. 8.3

Рис. 8.4

Уравнениями (8.2) определяется движение точки.

Движение точки М в одной плоскости определяется двумя урав­нениями движения (рис. 8.3):

. (8.3)

Прямолинейное движение точки М (рис. 8.4) определяется одним уравнением движения:

. (8.4)

Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметрические уравнения траектории точки. При исключении параметра t из уравнений движе­ния получаются уравнения траектории точки в координатной форме.

Пусть уравнения движения точки М имеют вид

.

Решив первое уравнение относительно t, получим

.

Подставив полученное для t выражение в два других уравнения, найдем уравнения траектории точки в координатной форме:

Как известно из аналитической геометрии, линии в пространстве соответствуют два уравнения с тремя координатами. Пусть движение точки М в плоскости задано уравнениями

.

Исключив параметр t, получим уравнение траектории точки в коор­динатной форме:

.

Помимо декартовых координат для определения положения точки на плоскости и в пространстве применяют и другие системы коор­динат (полярные, цилиндрические, сферические и др.).