3 Методы определения центров тяжести

Метод симметрии. При определении центров тяжести широко используется симметрия тел. Для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости сим­метрии. Для однородного тела, имеющего ось или центр симметрии, центр тяжести находится соответственно на оси симметрии или в центре симметрии.

Метод разбиения на части. Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны. В таких случаях центры тяжести сложных фигур вычисляются по общим формулам, определяющим центр тяжести, только вместо элементар­ных частиц тела берутся его конечные части, на которые оно разбито.

Пример 1. Определить координаты центра тяжести однородной пластины, показанной на рис. 7.3. Все размеры показаны на рисунке в сантиметрах.

Решение. Проводим оси координат и разбиваем пластину на три прямоугольника (линии разреза показаны пунктиром). Вычислим координаты центров тяжести ка­ждого из прямоугольников и их площади:

.

Площадь всей фигуры

.

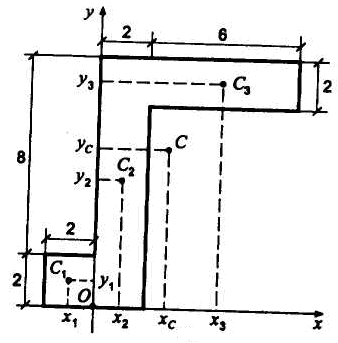
Рис. 7.3

Тогда,

,

.

Найденное положение центра тяжести совпадает с точкой С и показано на рис. 7.3.

Метод отрицательных масс. Проиллюстрируем этот метод на плоской фигуре.

Пример 2. Определить положение центра тяжести круглой пластины радиусом R с вырезом радиуса r (рис. 7.4). Расстояние .

Решение. Центр тяжести пласти­ны лежит на линии - на оси сим­метрии. Проводим оси координат, как показано на рис. 7.4.

Для нахождения координаты дополняем площадь пластины до полного круга, затем вычитаем из по­лученной площади площадь вырезан­ного круга . Тогда .

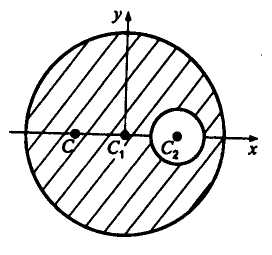
Рис. 7.4

Положение центра тяжести вычислим по формуле

Найденный центр тяжести лежит левее точки .

4 Центры тяжести простейших тел

Дуга окружности. Центр тяжести находится на оси симметрии дуги, которую примем за ось координат Ох (рис. 7.5). Координату центра тяжести дуги АВ вычисляем по формуле

. (а)

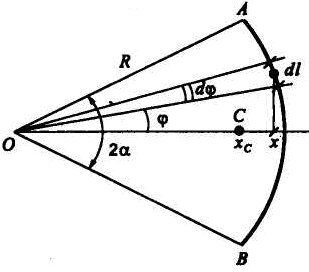
Рис. 7.5

Дуга окружности АВ, равная L, определяется радиусом R и стя­гиваемым ее центральным углом 2а В рассматриваемом случае

.

Подставляя эти значения в формулу (а), получим

.

Таким образом, .

Центр тяжести полукруга. Центр тяжести полукруга радиуса R (pис. 7.6) находится на оси симметрии, которую примем за ось Оу. Координату центра тяжести полукруга вычислим по формуле

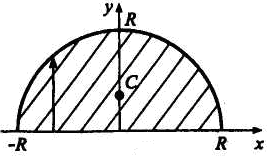
Рис. 7.6

.

В рассматриваемом случае

.

Имеем:

.

Подставляя эти значения в формулу для вычисления центра тя­жести полукруга , получим:

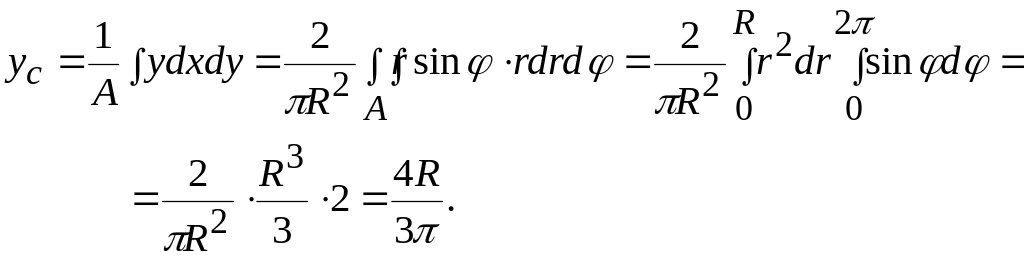
Таким образом, .

5 Статические моменты и центр тяжести

Рассмотрим плоскую фигуру площадью А и ограниченную некоторой кривой (рис. 7.7) в прямоугольной системе координат. Примем плотность тела , т.е. тогда масса любой части тела будет изме­ряться ее площадью. Это всегда подразумевается, когда говорят о статиче­ских моментах. Выделим в плоскости фигуры элемент площади dA с коор­динатами х и у (pис. 7.7) и определим статические моменты плоской фигуры, как взятые по всей площади А суммы произведений элементарных площадей dA на их расстояния х и у до осей Ох и Оу. Итак, статические моменты плоской фигуры определяются как

. (7.9)

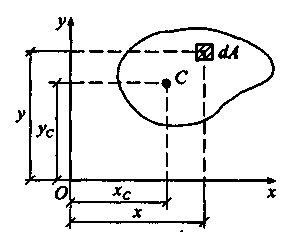
Рис. 7.7

Статические моменты обычно выражаются в см³ или м³.

При параллельном переносе осей значения статических момен­тов не остаются постоянными, а изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.

Ось, относительно которой статический момент равен нулю, называется центральной.

Точка пересечения центральных осей является центром тяжести сечения.

Если известны статические моменты площади фигуры относи­тельно координатных осей, то координаты ее центра тяжести можно определить по формулам

, (7.10)

где А - площадь сечения.

Пример 3. Вычислить центр тяжести плоской фигуры, изобра­женной на рис. 7.8. Размеры сечения на рисунке даны в сантиметрах.

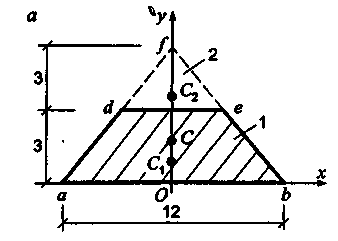
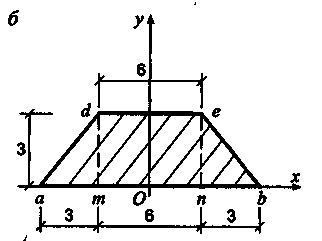
Рис. 7.8

Решение. Сечение имеет ось симметрии. Поэтому определяем только координату пользуясь методом разбиения на части. Допол­ним трапецию до треугольника abf u рассмотрим заданное сечение, состоящее из треугольников abf (часть 1) и def (часть 2) (рис. 7.8). При вычислении статического момента площадь треугольника def следует брать со знаком «минус», так как этот треугольник является дополнением к заданному сечению (трапеции).

Вычислим центр тяжести по формулам (7.9).

Определим статический момент трапеции относительно оси Ох.

.

Площадь сечения

.

Тогда

.

Статический момент можно также определить как сумму ста­тических моментов составляющих ее частей относительно той же оси Ох. Для этого разобьем трапецию на два одинаковых треуголь­ника amd (часть 1) и пbе (часть 2) и прямоугольник mden (часть 3) (рис. 7.8, б) и вычислим

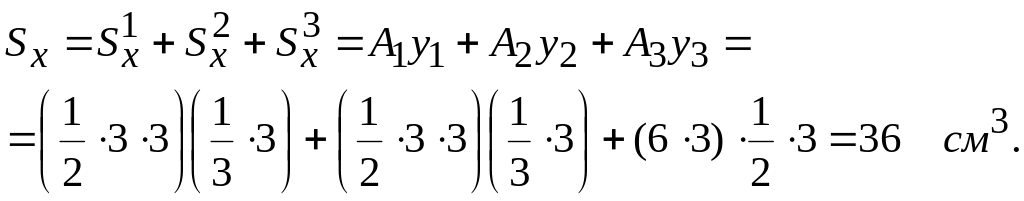
Координата центра тяжести имеет положительное значение, т. к. и, следовательно, должна быть отложена по оси Оу вверх.