2 Трение качения

Трение качения возникает в результате деформации катящегося тела и опорной поверхности, которые в действительности не являются абсолютно твердыми. Поэтому контакт между телом и поверхностью происходит по некоторой площадке (рис. 6.8, а). Нормальная реакция смещается относительно центра катка на некоторую величину в сторону движения, которая при выходе тела из равновесия достигает максимума и называется коэффициентом трения качения /к (рис. 6.8, б).

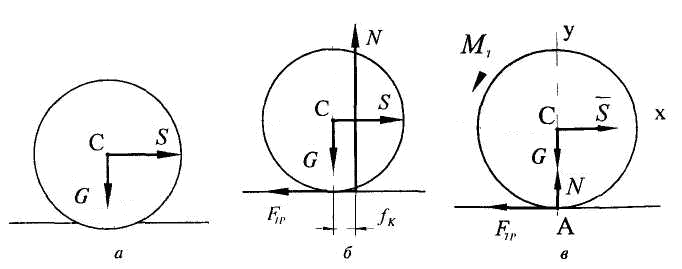
Рис. 6.8

Коэффициент трения качения имеет размерность длины в отличие от безразмерного коэффи­циента трения скольжения. Обычно нормальную реакцию про­водят через центр катка, добавляя при этом к телу пару сил с мо­ментом (рис. 6.9, в), который называют моментом трения качения:

.

Для катка, находящегося в покое, составим три уравнения равновесия (рис. 6.8, в):

1. .

2. .

3. .

.

Из последнего выражения получим условие качения колеса без скольжения.

Обычно это условие соблюдается. Поэтому для начала каче­ния катка требуется меньшая сила, чем для его скольжения.

Задача 2. Цилиндрический каток диаметра 60 см и весом Q = 3,92 кН приводится в равномерное движение человеком, который давит на рукоятку АО = 1,5 м с постоянной силой в направлении АО. Высота точки А над горизонтальной дорогой 1,2 м. Коэффициент трения качения катка равен = 0,5 см. Определить величину силы , силу трения при качении и нор­мальную составляющею реакции горизонтальной плоскости (рис. 6.9). Коэффициент трения скольжения между катком и дорогой = 0,2 .

Решение. Изобразим действующие на каток силы. (рис. 6.9, а).

Составим три уравнения равновесия для уравновешенной плоской произвольной системы сил:

, (6.5)

, (6.6)

. (6.7)

Рис. 6.9

Из (6.7) находим:

кН.

Из (6.6)

кН.

Из (6.5)

кН.

кН. .

Задача 3. Механическая конструкция (рис. 10.2.1), состоящая из груза весом Q = 15 кH опоры С, барабана весом P = 10 кH, и тормозного устройства, находится в покое, коэффициент сцепления f_сц между колодкой и барабаном равен 0,1. Определить значение силы и реакции опор О, А, В, приняв, что  = 30⁰; а = 10 см; в = 20 см.

Решение.

Составление расчётной схемы. Объектом равновесия является составная конструкция, состоящая из груза В, опоры С, барабана и тормозного устройства. Применим принцип освобождаемости от связей по всем связям системы (внешним и внутренним). При этом вместо конструкции получим три свободных тела (груз, барабан и тормозное устройство), находящихся в равновесии под действием системы сил. Опору С можно не принимать во внимание, так как активных сил к ней не приложено. Для каждого объекта равновесия необходимо составить расчетную схему в соответствии с известными правилами, собственно решение задачи начинаем с того объекта, к которому приложено меньшее количество неизвестных.

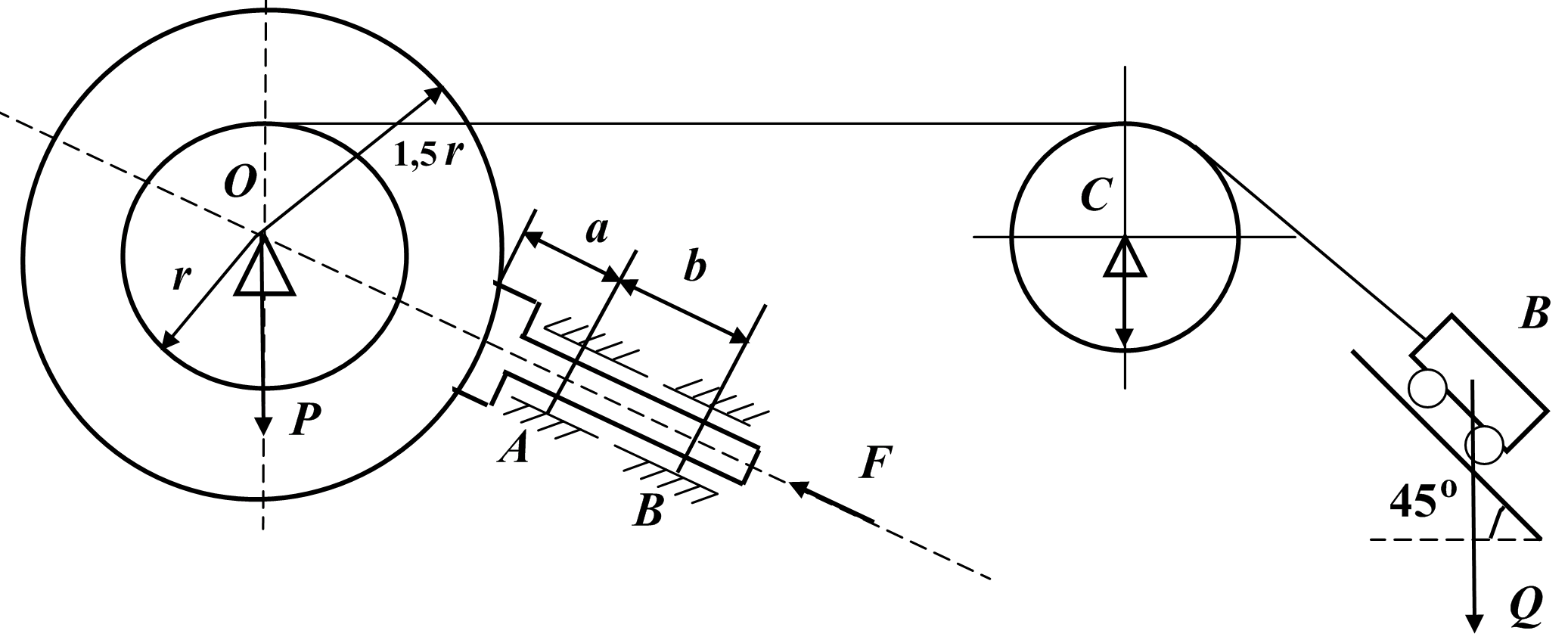
Рис. 10.2.1

1. Груз В

1.1. Составление расчётной схемы (рис. 10.2.2). Размерами груза В в процессе движения можно пренебречь, то есть считать его материальной точкой. Тогда объектом равновесия является узел В. Активной силой является сила тяжести Q. Применяя принцип освобождаемости от связей, мысленно отбросим связи (нить и идеальную поверхность) и заменим их действие реакциями и . Направление оси х принимаем по поверхности вниз, ось у – перпендикулярно оси х вверх.

Рис. 10.2.2

1.2. Условие равновесия. Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая системы сил равнялась нулю.

.

1.3. Составление уравнений равновесия.

; Q ∙ cos 45⁰ - T = 0 (1)

; N₁ – Q ∙ sin 45⁰ = 0 (2)

1.4. Определение неизвестных.

Из уравнения (1) Т = Q ∙ cos 45⁰.

Из уравнения (2) N₁ = Q ∙ sin 45⁰

2. Барабан

2.1. Составление расчетной схемы (рис. 10.2.3). Объектом равновесия является барабан. Активная сила – сила тяжести Р. Применяя принцип освобождаемости от связей, мысленно отбросим связи (нить и тормозное устройство) и заменим их действие реакциями Т′, N₂. Покажем силу сцепления F_сц, которая направлена по касательной к барабану, в сторону, противоположную возможному движению.

Рис. 10.2.3

2.2. Условия равновесия. Для равновесия плоской произвольной системы сил необходимой достаточно, чтобы главный вектор этой системы сил и её главный момент относительно любого центра были равны нулю.

.

2.3. Составление уравнений равновесия

; Т′ + F_сц ∙ cosα – N₂ ∙ sinα + R_Ox = 0; (3)

; N₂ ∙ cosα + F_сц ∙ sinα + R_Оy – P = 0; (4)

; -Т′ ∙ r + F_сц ∙ 1,5 ∙ r = 0. (5)

Сила сцепления F_сц между нормальной колодкой и барабаном определяется:

.

2.4. Определение искомых величин.

Решая систему уравнений (3 – 5), получим:

; T′ = T; ;

R_Ox = - T ′ – F_сц ∙ cosα + N₂ ∙ sinα;

R_Oy = - N₂ ∙ cosα – F_сц ∙ sinα + P.

.

3. Тормозное устройство

3.1. Составление расчётной схемы (рис. 10.2.4). Объект равновесия — шток тормозного устройства. Активная сила . Используя принцип освобождаемости от связей, мысленно отбросим связи (барабан и корпус тормозного устройства) и заменим их действие реакциями , , .

Покажем силу сцепления , равную по модулю и направленную в противоположную сторону. Направление оси х принимаем по оси штока вниз ось у – перпендикулярно оси х вправо.

3.2. Условия равновесия:

.

3.3. Составление уравнений равновесия:

; ; (6)

; ; (7)

; ; (8)

Рис. 10.2.4

3.4. Определение искомых величин, проверка правильности решения и анализ полученных результатов. Решая уравнения (6 – 8), получаем:

.

Подставляя числовые значения, получим:

.

.

Знак минус указывает на то, что реакция R_B направлена в сторону.

Задача 11.2.1. Цилиндрический каток диаметра 60 см и весом Q = 3,92 кН приводится в равномерное движение человеком, кото­рый давит на рукоятку АО = 1,5 м с постоянной силой в на­правлении АО. Высота точки А над горизонтальной дорогой 1,2 м. Коэффициент трения качения катка равен = 0,5 см. Определить величину силы , силу трения при качении и нор­мальную составляющею реакции горизонтальной плоскости (рис. 11.2.1, а). Коэффициент трения скольжения между катком и доро­гой = 0,2.

Рис. 11.2.1

Решение. При равномерном качении катка все силы, дей­ствующие на каток, уравновешиваются. К катку приложены две активные силы: вес катка и сила давления человека . На ка­ток наложена одна связь — горизонтальная плоскость. Применив закон освобождаемости от связей, отбросим мысленно горизон­тальную плоскость и заменим ее действие реакцией . Эта реак­ция приложена в точке С, находящейся на расстоянии от вер­тикали, проведенной через центр колеса. Реакция направлена по прямой СО, так как согласно теореме о трех непараллельных силах в случае равновесия линии их действия пересекаются в од­ной точке О (рис. 11.2.1, б). Реакцию плоскости раскладываем на две составляющие: нормальную составляющую , перпендикулярную к плоскости, и касатель­ную составляющую — силу трения при каче­нии , направленную вдоль плоскости.

Рассмотрим равно­весие катка как твер­дого тела, находящего­ся под действием четы­рех сил: , . Выберем систему декартовых координат. Ось х направим по го­ризонтальной плоскости вправо, ось у — вертикально вверх че­рез центр катка. Составим уравнения равновесия. Обозначив бук­вой а угол между горизонталью (осью х) и рукояткой ОА, по­лучим

, (1)

, (2)

. (3)

В уравнении (3) буквой r обозначен радиус катка.

При составлении суммы моментов сил относительно точки С сила , приложенная в центре катка О, разложена на две состав­ляющие — горизонтальную ( ) и вертикальную ( ), и использована теорема Вариньона. При этом, как принято всегда делать, при вычислении момента горизонтальной составляющей силы мы пренебрегли изменением ее плеча, считая, что оно равно радиусу катка r.

Из уравнения (3) найдем величину искомой силы :

кН.

Равенство (2) даст

кН.

Из уравнения (1) определяем величину силы трения:

кН.

Проверим, сопоставляя величины силы трения при качении , и силы трения скольжения, будет ли в данном случае чистое каче­ние или же будет иметь место скольжение. Сила трения скольже­ния равна

кН.

Таким образом, сила трения скольжения больше силы трения при качении

и каток будет катиться без скольжения.

Задача 11.2.2. Определить силу F, необходимую для равномерного качения катка радиусом r = 30 см и весом G = 300 кН по горизонтальной плоскости (рис. 11.2.2), если коэффициент трения качения f_к = 0,5 см, а угол α = 30°.

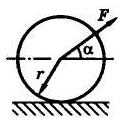
Рис. 11.2.2 Рис. 11.2.3

Решение. Первый вариант. Рассмотрим силы, действующие на каток (рис. 11.2.3). Сопротивление качению учтем за счет сме­щения нормальной реакции на величину f_к (первая мо­дель учета сопротивление качению). Составим уравнения для плоской системы сил:

Решив эту систему уравнений, найдем

Рис. 11.2.4

Второй вариант. Рассмотрим рас­четную схему (рис. 11.2.4), учитывая сопро­тивление качению за счет введения мо­мента сопротивления качению:

(*)

не смещая нормальную реакцию (вторая модель учета сопротивление качению).

Уравнения равновесия:

Решая эту систему уравнений, с учетом равенства (•), приходим к тем же результатам, что и в первом варианте.

3. Отметим, что для того, чтобы качение катка проис­ходило без проскальзывания, коэффициент трения сколь­жения должен быть достаточно большим, а именно:

и в нашем случае

Задача 11.2.3. Система состоит из двух цилиндров весом G₁ = 20 Н, и G₂ = 30 Н с одинаковыми радиусами R = 50 см, соединенных од­нородным стержнем веса G₃ = 40 Н. Цилиндры могут кататься без проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с трением качения.

Рис. 11.2.5

Коэффициент трения качения δ = 2 мм. К цилиндру 1 приложена пара с моментом М. К оси цилиндра 2 приложена наклонная сила F = 10 Н (рис. 11.2.5). В каких пределах меняется момент М в условии равновесия системы?

Решение

1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 11.2.7). Его величину находим по формуле М_тр = N₂ ∙δ.

2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 11.2.6, 11.2.7, 11.2.8). Внешние связи за­ меняем реакциями F_сц1, N₁, F_сц2, N₂.

Рис. 11.2.6 Рис. 11.2.7 Рис. 11.2.8

Реакции F_сц1 и F_сц2 приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей — Х₁, Y₁, Х₂, Y₂.

При составлении системы семи уравнений с неизвестными Х₁, Y₁, N₁, X₂, Y₂, N₂, M избегаем уравнения, в которые входят неизвестные реакции F_сц1 и F_сц2 .

Составляем уравнения равновесия для цилиндра 1 (рис. 11.2.6):

(1)

Уравнения равновесия цилиндра 2 (рис. 11.2.7) имеют вид

(2)

Уравнения равновесия стержня АВ (рис. 11.2.8) имеют вид

(3)

Из решения системы уравнений (1-3) определяем:

(4)

Радиус и коэффициент трения качения переводим в метры R = 0.5 м, δ = 0.002 м. Получаем М = 3.414 Нм. Вычисляем нормальные реакции опор:

N₁ = 36.058 Н, N₂ = 61.013 Н.

Убеждаемся, что N₁ > 0 и N₂ > 0, что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от по­верхности, отрицательной реакции опоры N ≤ 0 в задаче с односто­ронней связью не существует (физически не реализуется).

Рис. 11.2.9

3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Мо­мент трения качения направим против часовой стрелки (рис. 11.2.9). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы про­является только в знаке М во вто­ром уравнении равновесия (2). Так как М_тр = N₂∙8, то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения δ. Поэтому, не решая (и даже не со­ставляя) системы уравнений равнове­сия типа (1— 3) для нового направления возможного движения, записываем ответ, изменяя знаки у δ в (4):

(5)

Точно так же находим нормальные реакции опор: N₁ = 35.776 Н, N₂ = 61.295 Н. При равновесии системы момент, приложенный к цилиндру 1, изменяется в пределах (в Нм) (В задачах, где допускается проскальзывание, необходимо находить также силы F_cц1 и F_cц2 и проверять условие проскальзывания F_cц1 = F_тp1 < fN₁, F_cц2 = F_тp2 < fN₂, где f — коэффициент трения скольжения).

3.414 ≤ М ≤ 3.658.