Равновесие произвольной плоской системы сил
Плоская
произвольная система сил приводится к
главному вектору
и главному моменту
.
Для равновесия плоской произвольной
системы сил, приложенных к твердому
телу, необходимо и достаточно, чтобы
главный вектор и главный момент этой
системы сил равнялись нулю.
Условия равновесия в векторной форме:
.
Для произвольной плоской системы сил можно составить три уравнения равновесия.
Первая форма уравнений равновесия:
1.
.
2.
.
3.
.
Третье уравнение составляют относительно произвольной точки. Лучше всего брать точку, в которой имеется больше неизвестных реакций.
Вторая форма уравнений равновесия:
1. .
2.
.
3.
.
При использовании второй формы уравнений равновесия необходимо, чтобы ось х не была перпендикулярна прямой АВ.
Третья форма уравнений равновесия:
1. .
2.
.
3.
.
При использовании третьей формы уравнений равновесия необходимо, чтобы точки А, В, С не лежали на одной прямой.
Задача 8. Определить реакции опор, если F = 10 кН, q = 2 кН/м, М = 3 кНм (рис. 4.7).
Решение.
Рассмотрим равновесие балки АВ
под действием силы
,
момента
,
равномерно распределенной нагрузки и
реакций связей
.
Рис. 4.7
Составим три уравнения равновесия по
первой форме. Равномерно распределенную
нагрузку заменим равнодействующей
кН,
которая приложена в середине участка
BD:
1.
.
2.
.
3.
.
Находим из (1)
,
из (3)
,
из (2)
.
Ответ.
Минус
показывает, что направление
противоположно направлению, показанному
на рис. 4.7.
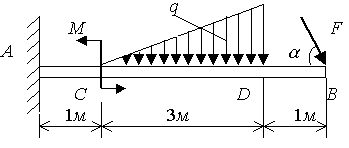
Задача 9. На балку с защемленным концом (рис. 4.2.1, а) действует распределенная по линейному закону нагрузка интенсивностью q = 0,2 кН/м. Сила F = 10 кH действует под углом α = 450 к оси балки, кроме того, приложена пара сил с моментом М = 4 кH∙м. Определить реакцию заделки.
Решение.
1.
Составление расчетной схемы (рис.
4.2.1, б).
Объектом равновесия
является балка АВ.
К
ней приложены активные силы
,
пара
сил с моментом
и
распределенная
по линейному закону нагрузка.
Равнодействующая
приложена
в точке О,
Связью,
наложенной на балку АВ,
является
жесткая заделка А.
Применяя
принцип освобождаемости от связей к
балке АВ,
заменим
действие
этой заделки на балку силами реакций
и
реактивным
моментом
.
Рассмотрим
теперь равновесие балки АВ
как
свободного твердого тела, на которое
действуют, кроме активных сил,
еще и реакции связи.
2. Условия равновесия:
.
а)
б)
Рис. 4.2.1
3. Составление уравнений равновесия. Для плоской произвольной системы сил условиям равновесия соответствуют три уравнения:
;
(а)
;
(б)
.
(в)
Для балки с жёсткой заделкой в качестве моментальной точки лучше брать заделку, что позволит исключить лишние неизвестные.
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.
Из уравнения (а) находим:
.
Из уравнения (б) получаем:
.
Наконец, из уравнения (в) находим:
Проверка. Составим уравнение моментов относительно точки В, подставим найденные реакции:
.
Положительные значения реакций связей подтверждают правильность выбранных направлений этих сил.
Задача 10. Определить реакции опор А и В балки, находящейся под действием одной сосредоточенной силы и пары сил. Нагрузка и размеры указаны на чертеже (рис. 4.2.2).
Решение.
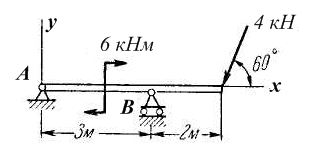
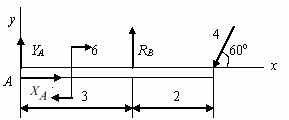
Рис. 4.2.2
кН,
кН
кН.