2. Точки перегиба графика функции.

Пусть функция дифференцируема на интервале , и – произвольная точка этого интервала. Предположим, что функция имеет определённое направление выпуклости на каждом из интервалов и .

Точка графика функции называется точкой перегиба этого графика, если существует такая окрестность точки , в пределах которой график функции имеет разные направления выпуклости.

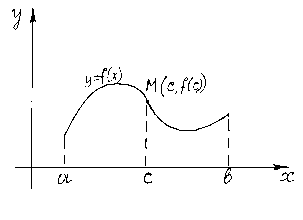
На рисунке изображён график функции, имеющей перегиб в точке .

Теорема 5.3. (Необходимое условие перегиба графика функции).

Если график функции имеет перегиб в точке и если функция имеет непрерывную вторую производную в точке , то .

Доказательство. Предположим обратное, т.е. предположим, что . Тогда в силу теоремы 5.2 существует такая окрестность точки , в пределах которой график функции (и слева и справа от ), имеет определенное направление выпуклости, а это противоричит наличию перегиба графика функции в точке . Полученное противоречие доказывает теорему.

Теорема 5.4. (Первое достаточное условие перегиба)

Пусть функция имеет вторую производную в некоторой окрестности точки и . Тогда, если в пределах указанной окрестности вторая производная имеет разные знаки слева и справа от точки , то график этой функции имеет перегиб в точке .

Доказательство. Так как вторая производная имеет разные знаки слева и справа от точки , то, согласно теореме 5.1, график функции имеет слева и справа от точки разные направления выпуклости, что означает наличие точки перегиба у графика функции в точке . Теорема доказана.

Теорема 5.5. (Второе достаточное условие перегиба).

Если функция имеет в точке конечную третью производную и удовлетворяет в этой точке условиям , то график этой функции имеет перегиб в точке .

Доказательство. Итак, , . Для определённости будем считать, что . Тогда по определению производной третьего порядка

Так как , то

.

По предположению, , поэтому существует такое, что для всех , для которых выполнены неравенства , справедливо неравенство .

Пусть, , тогда из неравенства (1) получим , т.е. вторая производная отрицательна слева от точки . Пусть теперь , тогда из неравенства (1) получим , т.е. вторая производная положительна справа от точки .

Итак, вторая производная имеет разные знаки слева и справа от точки . При этом

. Тогда по теореме 5.4, график функции имеет перегиб в точке . Аналогично рассматривается случай

44 Билет

Асимптоты графика функции.

Будем говорить, что прямая является вертикальной асимптотой графика функции , если хотя бы один из пределов или равен или .

Пример. График функции имеет вертикальную асимптоту , так как, ,

.

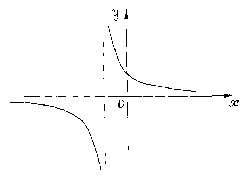
Прямая называется наклонной асимптотой графика функции при , если функция представима в виде

где .

Теорема 6.1. Для того чтобы прямая была наклонной асимптотой графика функции при необходимо и достаточно чтобы выполнялись следующие равенства:

Доказательство. Необходимость.

Пусть прямая является наклонной асимптотой графика функции при , тогда функция представима в виде

, где . Тогда

Рассмотрим теперь предел Следовательно, равенства (2) выполнены. Необходимость доказана.

Достаточность.

Пусть выполнены равенства (2). Тогда из существования предела следует, что разность является бесконечно малой функцией при . Следовательно, для функции справедливо представление (1). Теорема доказана.

В заключение данного параграфа приведём схему исследования графика функции.

Целесообразно провести следующие исследования:

Установить область определения функции.

Выяснить вопрос о существовании асимптот (вертикальных и наклонных)

Найти области возрастания и убывания функции и точки экстремума.

Найти области сохранения выпуклости и точки перегиба.

Найти точки пересечения графика функции с осями Ox и Oy.

После проведения указанных исследований легко строится эскиз графика функции. §7. Глобальные максимум и минимум функции на сегменте.

Пусть функция непрерывна на сегменте , тогда в силу второй теоремы Вейерштрасса существуют точки и сегмента такие, что .

Иными словами функция достигает в точке своего глобального максимума, а в точке - глобального минимума.

Естественно возникает вопрос: как найти точки глобального экстремума и .

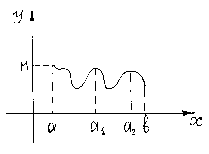
Приведём описание процесса нахождения глобального максимума M и соответствующей точки .

Пусть - какая-то точка глобального максимума. Указанная точка либо находится внутри сегмента либо совпадает с одной из точек a и b. Если находится внутри сегмента , то она совпадает с одной из точек локального максимума функции .

Предположим, что внутри сегмента существует конечное множество точек локального максимума функции . Пусть эти точки . Тогда очевидно, . В качестве точки можно взять тут точку из множества , в которой соответствующее значение функции будет наибольшим. Аналогично находится число m и соответствующая точка