21 Билет

Последовательность называется возрастающей, ; неубывающей, если ; убывающей, если ; невозрастающей, если

Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.

Теорема 3.10. Монотонная ограниченная последовательность сходится.

Рассмотрим случай неубывающей последовательности. Пусть для всех . Т.к. последовательность ограничена, то существует такое число , что для всех номеров справедливо неравенство . Пусть - множество, состоящее из элементов последовательности , т.е.

. Тогда - непустое, ограниченное сверху множество. Поэтому по теореме 2.1 для множества существует точная верхняя грань , т.е. . Докажем, что является пределом последовательности . Т.к. - точная верхняя грань множества , то такой элемент , что . С другой стороны, по определению точной верхней грани для всех . Из неравенств (22), (23) и из условия неубывания последовательности найдём

для всех .

Из последних неравенств имеем

для всех или для всех .

Т.е. является пределом последовательности .

Отметим, что аналогично доказывается теорема для случая невозрастающей ограниченной снизу последовательности.

5. Число . Рассмотрим последовательность с общим членом . Докажем, что последовательность является возрастающей и ограниченной сверху. Воспользуемся формулой бинома Ньютона.

,

где – число сочетаний из элементов по элементов и , где - факториал.

Тогда

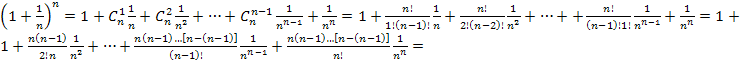
Т.е.

Тогда

Сравним и Легко заметить, что содержит на одно, положительное слагаемое больше, чем . Кроме этого для любого натурального , поэтому , Монотонное возрастание последовательности доказано. Докажем ограниченность последовательности . Заметим, что для любого натурального , поэтому

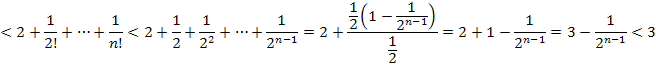
Т.е. для всех n. Тем самым, ограниченность последовательности доказано.

Итак, последовательность является монотонно возрастающей ограниченной сверху последовательностью.

В силу теоремы 3.10 последовательность сходится. Обозначим через .

Отметим, что число является иррациональным (без доказательства) числом, имеющим с точностью до пятнадцати знаков после запятой вид

22 Билет

Понятие функции. Пусть и - непустые числовые множества. Т.е. .

Если каждому элементу по некоторому закону ставится в соответствие единственный элемент , то говорят, что на множестве задана функция . При этом переменная называется аргументом или независимой переменной, множество называется областью определения функции. Совокупность всех значений называется областью изменения функции.

(Предел функции по Гейне). Число называется пределом функции в точке , если для любой сходящейся к последовательности значений аргумента , элементы которой отличны от , соответствующая последовательность сходится к числу .

(Предел функции по Коши). Число называется пределом функции в точке , если для любого положительного числа найдётся положительное число , такое, что для всех значений аргумента , удовлетворяющих условию справедливо неравенство

. Односторонние пределы.

Определение правого (левого) предела по Гейне. Число называется правым (левым) пределом функции в точке , если для любой сходящейся к последовательности , элементы которой больше (меньше) , соответствующая последовательность сходится к .

Для обозначения правого (левого) предела будем пользоваться обозначением: .

Определение правого (левого) предела по Коши. Число называется правым (левым) пределом функции в точке , если для любого существует такое, что для всех , удовлетворяющих неравенствам выполняется неравенство .

Легко установить эквивалентность приведенных двух определений односторонних пределов.

Рассмотрим в качестве примера функцию Эта функция не имеет предела в точке . Вместе с тем существуют как правый, так и левый пределы в точке , причем р

Действительно, для любой сходящейся к последовательности , элементы которой больше , а для любой сходящейся к последовательности , элементы которой меньше поэтому и .

Рассмотрим теперь сходящуюся к последовательность , в которой элементы с четными индексами больше, а нечетными меньше нуля. Тогда Очевидно, такая последовательность не имеет предела. Следовательно, в точке не имеет предела и функция

Теорема 4.1. Функция имеет в точке предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам

. Предел функции при и при .

Предел функции при по Гейне. Число называется пределом функции при , если для любой бесконечно большой последовательности значений аргумента , соответствующая последовательность значений функции сходится к числу .

Предел функции при по Коши. Число называется пределом функции при , если для любого положительного числа найдётся отвечающее ему положительное число такое, что для всех , удовлетворяющих неравенству , справедливо неравенство .

Не трудно доказать, что приведенные два определения эквивалентны.

Предел функции при (при ) по Гейне. Число называется пределом функции при ( ), если для любой бесконечно большой последовательности значений аргумента , все элементы которой положительны (отрицательны), соответствующая последовательность сходится к числу .

Предел функции по Коши. Число называется пределом функции при ( ), если для произвольного положительного числа , существует такое положительное число , что для всех значений аргумента , удовлетворяющих неравенству , справедливо неравенство

.

Для обозначения введённых понятий используем следующую символику:

.