
- •2 Билет
- •3 Билет
- •4 Билет
- •5 Билет
- •§3. Элементарные преобразования системы линейных алгебраических уравнений.
- •§5.Системы общего вида
- •§4. Системы с верхней трапециевидной матрицей.
- •§6. Однородные системы линейных алгебраических уравнений.
- •6.Декартовы координаты на прямой.
- •§2. Декартовы прямоугольные координаты на плоскости и в пространстве.
- •§3. Понятие вектора и линейные операции над векторами.
- •§4. Проекция вектора на ось и её свойства.
- •7. Определение скалярного произведения
- •8.1. Расстояние между двумя точками
- •2. Деление отрезка в данном отношении.
- •Полярная система координат.
- •9.1. Параметрические уравнения прямой.
- •2. Каноническое уравнение прямой в плоскости.
- •3. Общее уравнение прямой в плоскости.
- •4. Уравнение прямой в отрезках.
- •5. Неполные уравнения прямой.
- •6. Уравнение прямой, проходящей через заданные две точки.
- •10. . Уравнение прямой с угловым коэффициентом.
- •10.. Условия пересечения, коллинеарности и ортогональности двух прямых. Угол между двумя пересекающимися прямыми.
- •11 Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •16 Билет
- •17 Билет
- •18 Билет
- •19 Билет
- •20 Билет
- •21 Билет
- •22 Билет
- •23 Билет
- •24 Билет
- •25 Билет
- •26 Билет
- •27 Билет
- •28 Билет
- •29 Билет
- •30 Билет
- •31 Билет
- •32 Билет
- •33 Билет
- •34 Билет
- •35 Билет
- •36 Билет
- •37 Билет
- •38 Билет
- •39 Билет
- •40 Билет
- •2. Второе правило Лопиталя.
- •3. Другие виды неопределённостей и их раскрытие.
- •41 Билет
- •2. Другая запись формулы Тейлора и остаточного члена в форме пеано.
- •42 Билет
- •4. Разложение некоторых элементарных функций по формуле Маклорена.
- •43 Билет
- •2. Точки перегиба графика функции.
- •44 Билет
- •45 Билет
- •2. Неопределённый интеграл.
- •46 Билет
- •Интегрирование заменой переменной.
- •47 Билет
- •1. Площадь криволинейной трапеции.
- •48 Билет
- •49 Билет
- •§4. Основная формула интегрального исчисления.
- •50 Билет
- •Несобственный интеграл первого рода.
- •2. Несобственный интеграл II рода.
1 билет.
Основные
понятия и обозначения. Пусть
![]() .
Матрицей размера
.
Матрицей размера ![]() называется совокупность mn
чисел, записанных в виде прямоугольной
таблицы из m
строк и n
столбцов. При этом сами числа называются
элементами матрицы.
называется совокупность mn
чисел, записанных в виде прямоугольной
таблицы из m
строк и n
столбцов. При этом сами числа называются
элементами матрицы.
Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в скобки.
Элементы
матрицы обозначают строчными латинскими
буквами, снабженными двумя индексами:
![]() – элемент
матрицы, расположенный в i-й
строке и j-м
столбце или коротко элемент в позиции
– элемент
матрицы, расположенный в i-й
строке и j-м
столбце или коротко элемент в позиции
![]() .
.
В![]() общем виде матрица размера
может быть записана следующим образом
общем виде матрица размера
может быть записана следующим образом
Элементы
,
где ![]() ,
называются диагональными, а элементы
,
где
,
называются диагональными, а элементы
,
где ![]() – внедиагональными. Совокупность
диагональных элементов
– внедиагональными. Совокупность
диагональных элементов ![]() ,
где
,
где ![]() ,
называется главной диагональю матрицы.
,
называется главной диагональю матрицы.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается символом O
Заметим,
что для каждого размера ![]() существует
своя нулевая матрица.
существует
своя нулевая матрица.
Матрица
размера ![]() называется квадратной матрицей n-го
порядка. Квадратная матрица называется
диагональной, если все её внедиагональные
элементы равны нулю. Диагональная
матрица, у которой все диагональные
элементы равны 1, называется единичной
матрицей и обозначается символом I
или E.
называется квадратной матрицей n-го
порядка. Квадратная матрица называется
диагональной, если все её внедиагональные
элементы равны нулю. Диагональная
матрица, у которой все диагональные
элементы равны 1, называется единичной
матрицей и обозначается символом I
или E.
Линейные операции. Суммой двух матриц A и B размера называется матрица C размера , элементы которой определяются равенством
![]()
Сумму
матриц A
и B
будем обозначать ![]() .
.
Матрица
![]() называется противоположной к матрице
называется противоположной к матрице
![]() .
.
Теорема
2.1
Операция сложения матриц обладает
следующими свойствами: для любых матриц
![]() и нулевой матрицы
и нулевой матрицы ![]()
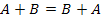 ;
(перестановочность или коммутативность
операции сложения
;
(перестановочность или коммутативность
операции сложения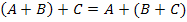 ;
(ассоциативность или сочетательное
свойство)
;
(ассоциативность или сочетательное
свойство)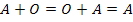
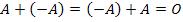
Док-во (4):
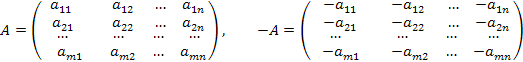
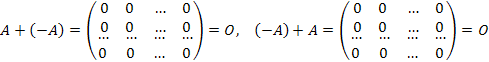
Разностью
матриц
и ![]() называется матрица
называется матрица ![]() .
Разность матриц A
и B
будем обозначать
.
Разность матриц A
и B
будем обозначать ![]() .
.
Произведением
матрицы
на число α
называется матрица ![]() ,
элементы которой определены равенством
,
элементы которой определены равенством
![]()
Произведение
матрицы A
на число ![]() будем обозначать
будем обозначать ![]() .
.
Теорема 2.2. Операция умножения матрицы на число обладает следующими свойствами:
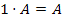
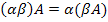
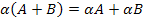 (Распределительное свойство относительно
сложения матриц);
(Распределительное свойство относительно
сложения матриц);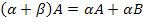 (Распределительное свойство относительно
сложения чисел);
(Распределительное свойство относительно
сложения чисел);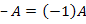 .
.
2 Билет
Умножение
матриц.
Произведением матриц
и ![]() называется матрица
называется матрица ![]() ,
элементы которой определены равенством
,
элементы которой определены равенством
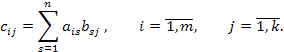
Произведение
матриц A
и B
будем обозначать ![]() .
.
Из
определения следует, что произведение
![]() определено лишь в том случае, когда
число столбцов матрицы A
совпадает с числом строк матрицы B.
Это означает, что оба произведения AB
и BA
определены тогда и только тогда, когда
матрицы A
и B
имеют размеры
и
определено лишь в том случае, когда
число столбцов матрицы A
совпадает с числом строк матрицы B.
Это означает, что оба произведения AB
и BA
определены тогда и только тогда, когда
матрицы A
и B
имеют размеры
и ![]() соответственно. Следовательно равенство
соответственно. Следовательно равенство
![]() возможно лишь для квадратных матриц
одинакового порядка. Однако и в этом
случае произведение матриц, вообще
говоря, зависит от порядка сомножителей.
возможно лишь для квадратных матриц
одинакового порядка. Однако и в этом
случае произведение матриц, вообще
говоря, зависит от порядка сомножителей.
![]() ,
тогда
,
тогда
![]() .
.
Следовательно
![]() .
.
Матрицы A и B называются перестановочными или коммутирующими, если .
Теорема 2.3. Операция умножения матриц обладает следующими свойствами:
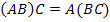 (Свойство ассоциативности),
(Свойство ассоциативности),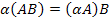 ,
для любого действительного числа α,
,
для любого действительного числа α,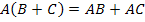 ,
,
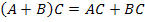 (Свойство дистрибутивности),
(Свойство дистрибутивности),
для любых матриц A,B,C, для которых левые части равенств имеют смысл.
Справедливость
свойств 2) и 3) доказываются непосредственно.
В качестве иллюстрации приведём
доказательство первого равенства
свойства 3). Пусть
,
,
![]() .
Матрицы
.
Матрицы ![]() и
и ![]() имеют одинаковый размер -
имеют одинаковый размер - ![]() .
Пусть
.
Пусть ![]() – элемент матрицы
в позиции
,
– элемент матрицы
в позиции
,
![]() - элемент матрицы
в позиции
,
тогда
- элемент матрицы
в позиции
,
тогда
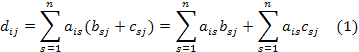
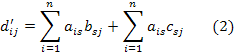
Из
равенств (1) и (2) следует, что ![]() ,
что доказывает первое равенство свойства
3).
,
что доказывает первое равенство свойства
3).
Транспонирование
матриц. Пусть
.
Матрица ![]() называется транспонированной к матрице
A,
если
называется транспонированной к матрице
A,
если
![]()
Транспонированная
матрица также обозначается символами
![]() и
и ![]() .
.
Заметим,
что при транспонировании матрицы её
строки становятся столбцами матрицы
![]() ,
с теми же номерами, а столбцы – строками.
,
с теми же номерами, а столбцы – строками.
Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами:
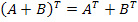 ,
,
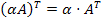 ,
для любого действительного числа α,
,
для любого действительного числа α,
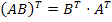 ,
, ,
,
для любых матриц A и B, для которых имеют смысл левые части равенств.
Свойства
1), 2), 4) непосредственно вытекают из
определения. Приведём доказательство
свойства 3). Пусть
и
,
при таком согласовании размеров матриц
A
и B
произведения AB
и ![]() существуют, при этом размеры
существуют, при этом размеры ![]() и
и
совпадают и равны ![]() .
Пусть
- элемент матрицы
.
Пусть
- элемент матрицы ![]() в позиции
,
в позиции
,
![]() – элемент матрицы
,
- элемент матрицы
в позиции
.
– элемент матрицы
,
- элемент матрицы
в позиции
.

что доказывает справедливость свойства 3).
3 Билет
Понятие
определителя квадратной матрицы ![]() ,
для
,
для ![]() .
.
Определитель
– это некоторое число поставленное в
соответствие квадратной матрице ![]() .
.
Для неквадратных матриц понятие определителя не вводится.
Для
обозначения определителя квадратной
матрицы A
будем пользоваться обозначением ![]() или det
A
или det
A
Пусть A
- произвольная квадратная матрица
порядка n.
Если ![]() ,
то матрица A
состоит из одного числа A
Положим по определению, что определитель
такой матрицы равен числу A,
т.е.
,
то матрица A
состоит из одного числа A
Положим по определению, что определитель
такой матрицы равен числу A,
т.е. ![]() .
Если
.
Если ![]() ,
то матрица A
имеет
вид
,
то матрица A
имеет
вид
![]()
Положим по определению, что определитель такой матрицы равен
![]()
Если
![]() ,
то матрица A
имеет вид
,
то матрица A
имеет вид

Положим по определению, что определитель такой матрицы равен
![]()
Основные свойства определителей.
Свойство
1. Определитель
квадратной матрицы не изменяется при
её транспонировании: ![]() .
.
Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка.
Пусть
![]()
![]()
Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю.
Свойство 2 непосредственно вытекает из определения определителя.
Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.
Доказательство свойства 3 приведём для квадратных матриц третьего порядка. Пусть
Пусть B - матрица, полученная из матрицы A перестановкой мест первых двух строк, т.е.
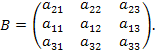
![]()
![]()
Аналогично проходит доказательство свойства 3, при перестановке любых других строк (столбцов).
Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.
Доказательство
свойства 4 приведём для случая умножения
элементов первой строки, квадратной
матрицы третьего порядка, на произвольное
число
![]() .
.
Пусть
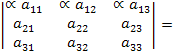
![]()
Аналогично доказывается свойство 4 для всех остальных случаев.
Свойство
5. Если
каждый элемент i-й
строки (столбца) матрицы A
представлен в виде суммы двух слагаемых,
то определитель такой матрицы равен
![]() ,
где элементы матриц B
и C,
за исключением элементов -й строки
(столбца), совпадают с соответствующими
элементами матрицы A.
А в
,
где элементы матриц B
и C,
за исключением элементов -й строки
(столбца), совпадают с соответствующими
элементами матрицы A.
А в ![]() -х
строках (столбцах) матриц B
и C
стоят упомянутые первые и вторые
слагаемые соответственно.
-х
строках (столбцах) матриц B
и C
стоят упомянутые первые и вторые
слагаемые соответственно.
Доказательство свойства 5 приведём для случая, когда элементы первой строки квадратной матрицы второго порядка, представлены в виде двух слагаемых.
Пусть
![]() .
.
![]()
![]()
![]()
Аналогично доказывается свойство 5 и для квадратных матриц третьего порядка.
Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя.
Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю.
Доказательство.
Пусть
A
- квадратная матрица, имеющая две
одинаковые строки (столбца). B
- матрица полученная в результате
перестановки указанных одинаковых
строк (столбцов) матрицы A.
Тогда, с одной стороны, ![]() ,
с другой стороны, в силу свойства 3,
,
с другой стороны, в силу свойства 3, ![]() .
Следовательно,
.
Следовательно, ![]() .
Из последнего равенства следует, что
.
Из последнего равенства следует, что
![]() .
.
Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю.
Доказательство. Пусть A - квадратная матрица третьего порядка, имеющая две пропорциональные строки.
Будем считать, без ограничения общности, что в матрице A пропорциональны две строки. Предположим, что элементы второй строки получены умножением соответствующих элементов первой строки на некоторое число .
![]()
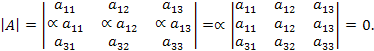
Следствие 3. Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число , то определитель не изменится.
Доказательство. Пусть A - квадратная матрица третьего порядка
В качестве иллюстрации доказательства, рассмотрим случай, когда к элементам первой строки матрицы A прибавляются элементы второй строки, умноженные на произвольное число . Тогда, в силу свойства 5 и следствия 2
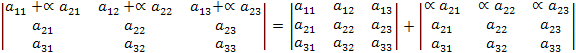 =
=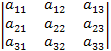
Миноры
и алгебраические дополнения. Пусть
A
- произвольная квадратная матрица,
– её элемент, стоящий в позиции
.
Вычеркивая из матрицы A
i-ю
строку и -ый столбец, получим некоторую
матрицу ![]() ,
порядка
,
порядка ![]() .
Определитель матрицы
называется минором элемента
.
Минор элемента
будем обозначать символом
.
Определитель матрицы
называется минором элемента
.
Минор элемента
будем обозначать символом ![]() .
.
Число
![]() называется алгебраическим дополнением
элемента
.
Для обозначения алгебраического
дополнения элемента
будем пользоваться символом
называется алгебраическим дополнением
элемента
.
Для обозначения алгебраического
дополнения элемента
будем пользоваться символом ![]() .
.
Разложение определителя по строке (столбцу)
Теорема 4.1. Определитель квадратной матрицы равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения.
В качестве иллюстрации докажем, что определитель любой квадратной матрицы третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения. Пусть.
Рассмотрим сумму произведений элементов первой строки на их алгебраическое дополнение
![]()
![]()
Легко заметить, что правая часть равенства (3) равна определителю матрицы A.
