1. Площадь криволинейной трапеции.
Пусть на сегменте задана неотрицательная и непрерывна функция .
Фигуру,
ограниченную линиями 
,
отрезком
оси Ox
и графиком функции
назовём криволинейной трапецией. Площадь
указанной криволинейной трапеции
обозначим через S. Тогда
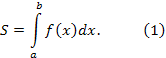
Доказательство.
Возьмём произвольное разбиение сегмента
.
Выберем на каждом частичном сегменте
произвольную точку
.
Для данного разбиения и данного выбора
точек
составим интегральную сумму функцию
f(x)
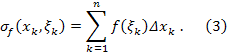
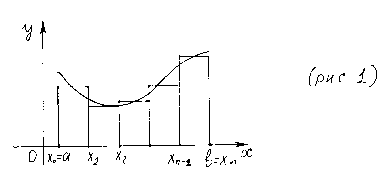Интегральная
сумма (3) равна площади ступенчатой
фигуры, указанной на рис. 1. Площадь
криволинейной трапеции приблизительно
равна площади ступенчатой фигуры
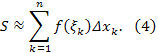
Естественно полагать, что площадь ступенчатой фигуры стремится к площади криволинейной трапеции при стремлении к нулю наибольшей длины частичных сегментов разбиения (2). Таким образом
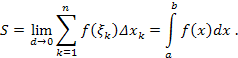
Равенство (1) доказано.
Замечание.
В случае, когда график функции
задан параметрическими уравнениями
,
получим
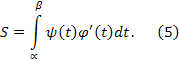
48 Билет
Если
функция
интегрируема на сегменте
и 
всюду на сегменте
,
то
.
Доказательство. Очевидно, что любая интегральная сумма
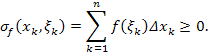
Следовательно,
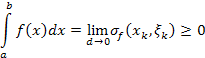
5) Если
функции
и
интегрируемы на сегменте
и в каждой точке данного сегмента
выполнено неравенство 
,
то
Действительно,
рассмотрим функцию 
;
тогда эта функция интегрируема и
неотрицательна на сегменте
.
Пользуясь
свойствами 2) и 4), получим
Что доказывает справедливость неравенства (6).
Прежде
чем перейти к формулировке следующего
свойства, вычислим 
Пользуясь определением определённого интеграла, находим
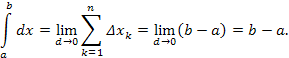
Таким образом, справедливо равенство
.
(7)
6)
Формула
среднего значения.
Пусть функция
интегрируема на сегменте
,
a
M
и m
– точные верхняя и нижняя грани функции
на этом сегменте. Тогда существует
число 
,
такое, что справедливо равенство
(8)
Доказательство.
Прежде всего заметим, что из условия
интегрируемости функции
на сегменте
следует ограниченность этой функции
на указанном сегменте. Пусть 
точная
верхняя и точная нижняя грани функции
на сегменте
.
Очевидно,
в каждой точке 
выполняются неравенства
Пользуясь свойством (5) и равенством (7), получим
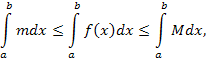
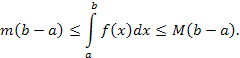
Из последних неравенств получаем
Введем обозначение
Из
неравенств (9) следует, что для числа
выполнены неравенства 
.
Умножив обе части равенства (10) на 
,
мы получим требуемое равенство (8).
7) Формула среднего значения для непрерывной функции.
Если функция непрерывна на сегменте , то существует точка принадлежащая сегменту такая, что
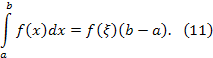
Доказательство.
Так как функция
непрерывна на сегменте
,
то в силу теоремы 1.2.главы 9, она интегрируема
на сегменте
.
Следовательно, справедливо равенство
(8). Для завершения доказательства
равенства (11) нам остаётся применить
теорему 5.4. главы 5. (Теорема о прохождении
непрерывной на сегменте функции через
любое промежуточное значение). Согласно
этой теореме существует точка
сегмента
такая, что 
.
8) Если функция интегрируема на сегменте , то справедливо следующее неравенство
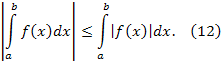
Доказательство. В силу теоремы 1.3 функция интегрируема на сегменте . Очевидно, что для любой точки x сегмента справедливы равенства
Из последних неравенств и свойства (6) получим неравенства
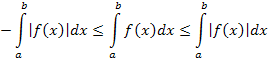
что доказывает справедливость неравенства (12).