5 Билет

Понятие ранга матрицы. Пусть - произвольная матрица размера , - произвольное натуральное число, удовлетворяющее неравенству . Выберем в матрице произвольные строк и столбцов с номерами и соответственно. Элементы матрицы , стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка, расположенным в строках с номерами и столбцах с номерами .

Для обозначения минора будем пользоваться символом или .

Рангом ненулевой матрицы называется максимальный порядок ненулевых миноров этой матрицы. Ранг нулевой матрицы по определению считается равным нулю.

Ранг матрицы будем обозначать символами

.

Из определения ранга матрицы вытекают следующие факты:

1.Ранг матрицы не превосходит её размеров: есл , то

2.Равенство равносильно выполнению двух условий: а) в матрице A существует ненулевой минор порядка r; б) любой минор более высокого порядка (если такой существует) равен нулю.

Пусть . Любой ненулевой минор порядка называется базисным минором. Строки и столбцы матрицы , в которых расположен базисный минор называются базисными строками и столбцами.

Теорема 6.1. При транспонировании матрицы её ранг не изменяется.

Теорема 6.2. Элементарные преобразования матрицы не изменяют её ранга.

Теорема 6.3. Ранг трапециевидной матрицы равен числу её ненулевых строк.

Метод Гаусса вычисления ранга. Теоретическую основу этого метода составляют,

доказанные выше, теоремы 6.2 и 6.3. Суть метода Гаусса вычисления ранга матрицы состоит в приведении этой матрицы элементарными преобразованиями к верхней трапециевидной форме и подсчете ненулевых строк полученной трапециевидной матрицы.

Системой линейных алгебраических уравнений с неизвестными называется совокупность соотношений

где , - заданные числа, а - неизвестные величины. Числа называются коэффициентами системы, а – свободными членами. При этом предполагается, что хотя бы один из коэффициентов отличен от нуля.

Упорядоченная совокупность чисел называется решением системы (1), если при подстановке этих чисел в систему вместо неизвестных соответственно, каждое уравнение системы обращается в тождество.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.

Система (1) называется определённой, если она имеет единственное решение, и неопределённой, если имеет более одного решения.

Исследовать и решить систему – это значит

а) Установить, совместна она или несовместна;

б) Если она совместна, установить, является она определённой или неопределённой, при этом

- в случае определённой системы найти единственное её решение;

- в случае неопределённой системы описать множество всех её решений.

Компактная запись системы.

Рассмотрим матрицу , составленную из коэффициентов системы (1). Матрица называется основной матрицей системы (1).

Пусть - матрица столбец, составленная из свободных членов, а – матрица столбец, составленная из неизвестных . Тогда система (1) может быть записана в виде

Уравнение (2) называется матричной формой записи системы (1).

Приписав к основной матрице столбец свободных членов , получим матрицу

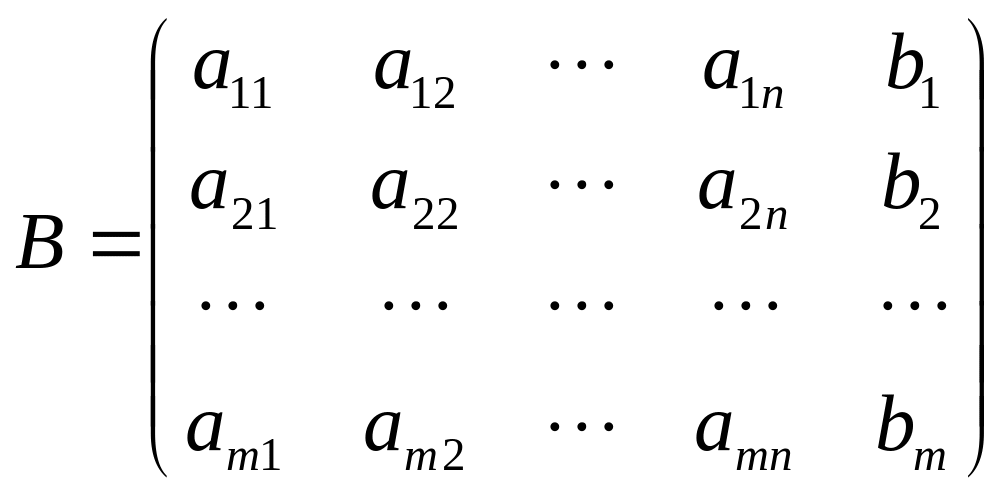
размера .

Матрица называется расширенной матрицей системы (1).

Системы с квадратной невырожденной матрицей.

Рассмотрим системы линейных алгебраических уравнений, состоящей из уравнений и неизвестных .

Пусть - основная матрица системы (1), - столбец неизвестных и – столбец свободных членов.

Запишем систему (1) в матричной форме

Теорема 2.1. Система линейных алгебраических уравнений с квадратной невырожденной матрицей совместна и имеет единственное решение.

Правило Крамера. При доказательстве теоремы 2.1 была получена матричная форма записи решения системы (1). . Учитывая, что

получим

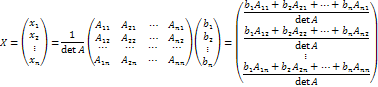
Следовательно

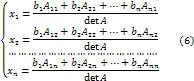
Введём следующие обозначения

Заметим, что определители отличаются от определителя только i-ым столбцом. На месте i-го столбца стоит столбец свободных членов .

Раскладывая определитель по первому столбцу, определитель по второму столбцу и т.д. Определитель по последнему столбцу, получим

Учитывая равенства (7) в равенствах (6) мы получим

Формулы (8) называются формулами Крамера.