4 Билет

Квадратная матрица называется диагональной, если все её внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Квадратная матрица называется верхней треугольной, если при , и нижней треугольной, если при . Общий вид треугольных матриц:

.

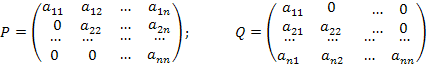Вычисление определителя. Во многих задачах линейной алгебры возникает необходимость вычисления определителя.

Среди различных методов вычисления определителя особое место занимает метод Гаусса.

Суть метода Гаусса вычисления определителя состоит в следующем:

1. Привести элементарными преобразованиями данную квадратную матрицу к треугольному виду. При этом такие преобразования либо не изменяют определителя матрицы, либо изменяют его контролируемым образом;

2. Вычислить определитель треугольной матрицы;

3. Восстановить исходный определитель.

Теорема 4.3. ^** Определитель произведения квадратных матриц A и B равен произведению определителей матриц-сомножителей, т.е.

Условие обратимости. Матрица называется обратной к матрице A, если , где I - единичная матрица. Матрица A, для которой существует обратная матрица, называется обратимой.

Так как равенство возможно лишь для квадратных матриц одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима.

Квадратная матрица A называется вырожденной, если , и невырожденной, если .

Теорема 5.1. (Критерий обратимости) Матрица A обратима тогда и только тогда, когда она не вырождена.

Доказательство. Пусть A обратимая. Тогда существует матрица такая, что . Из этого равенства и теоремы 4.3 следует, что . Следовательно , т.е. матрица A не вырождена.

Пусть теперь матрица A не вырождена. Рассмотрим вспомогательную матрицу

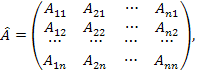
где  – алгебраическое дополнение элемента матрицы A. Матрица называется присоединённой или взаимной к матрице A. Покажем, что матрица является обратной к матрице A. Тем самым будет доказана обратимость матрицы A.

Рассмотрим матрицу . В позиции матрицы стоит элемент ,

. Из теоремы 4.4. и определения определителя n-го порядка следую, что при и при . Следовательно

.

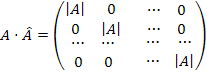Из последнего равенства следует, что .

Совершенно аналогично доказывается, что

, т.е. .

(О единственности обратной матрицы) Если A - квадратная невырожденная матрица, то существует единственная обратная к ней матрица.

Доказательство. Т.к. матрица A невырождена, то в силу теоремы 5.1, она обратима, при этом матрица является обратной к матрице A

Пусть B - произвольная матрица, удовлетворяющая равенствам . Единственность обратной матрицы будет доказана, если .

Умножая равенство слева на матрицу , получим

, (1)

С другой стороны

= . (2)

Сравнивая равенства (1) и (2) приходим к выводу .

Определитель любой верхней треугольной (нижней треугольной) матрицы равен произведению диагональных элементов.

Определитель любой диагональной матрицы равен произведению диагональных элементов.

(обратимость призведения двух невырожденных матриц) Пусть квадратные невырожденные матрицы порядка n. Тогда матрица обратима и при этом

Доказательство. В силу теоремы 4.3 . Т.е. матрица AB - невырождена. Следовательно, в силу теоремы 5.1 обратима.

Рассмотрим матрицу

Рассмотрим теперь матрицу

Из равенств (3), (4) и определения обратной матрицы следует, что .