11 Билет

Пучок прямых, уравнение пучка прямых.

Множество всех прямых плоскости, проходящих через данную точку , будем называть пучком прямых, проходящих через точку .

Пучок прямых, проходящих через точку будем обозначать .

Рассмотрим множество всевозможных прямых, проходящих через некоторую точку и не параллельных оси . Пусть – уравнение произвольной прямой из указанного множества. Тогда . Подставляя найденное выражение для коэффициента b в уравнение прямой, получим

Уравнение любой прямой, проходящей через точку и не параллельной оси Oy, получается из уравнения (42) при соответствующем подборе углового коэффициента k. Это уравнение называется уравнением пучка прямых, проходящих через точку

Пусть прямые заданные общими уравнениями

пересекаются в единственной точке .

Справедлива следующая теорема:

Теорема 2.2. Для того, чтобы прямая ,заданная общим уравнением принадлежала пучку прямых, проходящих через точку , необходимо и достаточно, чтобы существовали такие действительные числа и β, , что , , .

Доказательство. Докажем сначала достаточность.

Пусть выполнены равенства (45) Докажем, что прямая L принадлежит пучку . Для этого достаточно доказать справедливость равенства

Так как, точка принадлежит как прямой , так и прямой , то её координаты , удовлетворяют равенствам

. (46)

Рассмотрим выражение . Подставляя в место коэффициентов соответствующие выражения из равенств (45), получим

Достаточность доказана.

Докажем необходимость. Пусть прямая L, задана её общим уравнением принадлежит пучку , т.е. проходящих через точку .

Покажем, что существуют такие действительные числа и β, , что верны равенства (45).

Пусть произвольная, отличная от , точка прямой L. Положим . Поскольку точка не может одновременно лежать на , то по крайней мере одно из чисел или отлично от нуля.

Рассмотрим прямую заданную уравнением

(47)

Из равенств

.

Следует, что точки и лежат на прямой, заданной уравнением (47).

Так как, через две различные точки и проходит единственная прямая, то прямая L совпадает с прямой, заданной уравнением (47). Необходимость доказана.

Из теоремы следует, что прямая L с общим уравнением принадлежит пучку прямых, проходящих через точку пересечения двух прямых

Тогда и только тогда, когда уравнение прямой можно представить в виде

Заметим, что уравнение любой прямой, проходящей через точку пересечения прямых можно получить путём соответствующего подбора и β.

В частности, если , , мы получим уравнение прямой . Если , мы получим уравнение прямой .

12 Билет

Нормированное уравнение прямой. Расстояние от точки до прямой.

Нормированным уравнением прямой называется уравнение вида , которое получается из общего уравнения путём деления его на длину нормального вектора .

Расстояние от точки до прямой.

Докажем, что расстояние точки до прямой, заданной общим уравнением равно

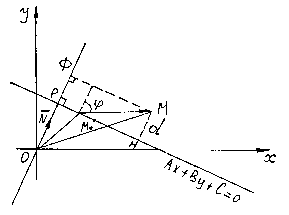
Доказательство. Рассмотрим на плоскости произвольную прямую L, определяемую общим уравнением и вектор .

Единичный вектор коллинеарен вектору , а поэтому ортогонален к прямой L. Приложим вектор к началу координат. Пусть P - точка пересечения прямой, на которой лежит вектор и прямой L. Возьмём на плоскости произвольную точку , а на прямой L -произвольную точку . Пусть – проекция точки M на прямую, на которой лежит вектор . Тогда очевидно, что и будет расстоянием от точки до прямой L. Пусть - угол между векторами и тогда