31 Билет

Производная. 1. Приращение аргумента и функции. Разностная форма условия непрерывности.

Пусть функция определена на некотором интервале . Фиксируем любое значение x из указанного интервала. Пусть приращение такое, что значение также принадлежит интервалу . Приращением функции в точке x, соответсвующим приращению аргумента назовем число .

Из определения непрерывной функции следует, что функция непрерывна в точке x тогда и только тогда, когда . Т.е. функция непрерывна в точке x тогда и только тогда, когда является бесконечно малой функцией при .

2. Определение производной.

Считая, что , рассмотрим отношение приращения функции к соответствующему приращению аргумента

Выражение в правой части равенства (2) называется разностным отношением функция в точке x. Поскольку значение x считаем фиксированным, то разностное отношение (2) представляет собой функцию от аргумента . Эта функция определена для всех значений аргумента , принадлежащих некоторой достаточно малой окрестности точки , за исключением самой точки . Таким образом, мы можем рассмотреть вопрос о существовании предела разностного отношения (2) при .

Если существует предел разностного отношения в точке x при , то значение этого предела называется производной функции в точке x и обозначается .

Итак, по определению

3. Геометрический смысл производной.

Пусть функция определена на интервале и имеет в данной точке x интервала производную . Пусть точка M на графике функции соответствует значению аргумента x, а точка P - значению .

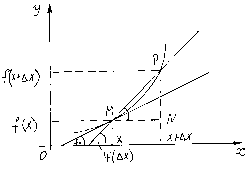
Проведём через точки M и P прямую и назовём её секущей. Обозначим через угол между секущей и осью .

Касательной Sк графику функции в точке M будем называть предельное положение секущей MP при или, что тоже самое при P->M

Из определения следует, что для существования касательной в точке M достаточно, чтобы существовал предел . Заметим, что если указанный предел существует, то значение этого предела равено углу наклона касательной к оси .

Справедливо следующее утверждение.

Если функция имеет в данной фиксированной точке производную, то существует касательная к графику функции в точке , причём угловой коэффициент этой касательной равен производной .

Докажем сформулированное выше утверждение. Из треугольника MNP находим

Таким образом,

Так как функция имеет производную в точке x, то существует . Отсюда в силу непрерывности функции следует существование предела При этом, из равенства (4) имеем

.

Следовательно, существует предельное положение секущей. Тем самым доказано существование касательной к графику функции в точке , причём угол наклона этой касательной к оси равен Из этого равенства находим . Таким образом, угловой коэффициент касательной равен

Пусть в некоторой точке существует производная . В силу доказанного выше утверждения к графику функции в точке существует касательная при этом, угловой коэффициент этой касательной равен . Тогда уравнение касательной, проведенной к графику функции в точке имеет вид: .

4. Физический смысл производной.

Предположим, что функция описывает закон движения материальной точки M по прямой линии, т.е. - путь, пройденный точкой M от начала отсчёта за время x. Тогда за время пройден путь , а за время x1- путь . За промежуток времени точка M пройдёт отрезок пути . Отношение называется средней скоростью движения за время , а предел при определяет мгновенную скорость точки M в момент времени .

5. Правая и левая производные.

Правой (соответственно левой) производной функции в данной фиксированной точке называется правый (соответственно левый) предел разностного отношения при (если этот предел существует).

Правую производную обозначим символом , левую - .

Следовательно

Заметим, что если существует производная в точке x, то существуют правая и левая производные, при этом . И обратно, если существуют левая и правая производные функции в точке x и эти производные совпадают, то существует и производная в точке и эта производная совпадает с правой и левой производными в точке x

Теорема 1.1. Для того чтобы функция была дифференцируемой в данной точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную

Теорема 1.2. Если функция дифференцируема в данной точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то её приращение можно представить в виде , где A– постоянная, не зависящая от , а - бесконечно малая функция при . Тогда . Из последнего равенства следует непрерывность функции .

Заметим, что обратное утверждение неверно. Функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.

Пример. Функция непрерывна в точке 0, однако, как было показано выше, у этой функции не существует производной в точке 0. Следовательно, эта функция не дифференцируема в точке 0.