27 Билет

Функция называется непрерывной в точке , если в этой точке существует предел функции и этот предел равен

(Определение непрерывной функции по Гейне) Функция называется непрерывной в точке , если для любой последовательности значений аргумента , сходящейся к , последовательность сходится к .

(Определение непрерывной функции по Коши) Функция называется непрерывной в точке , если для любого положительного существует такое положительное число , что как только , справедливо неравенство .

Арифметические операции над непрерывными функциями.

Теорема 5.1. Пусть функции и непрерывны в точке . Тогда функции

и , также непрерывны в точке .

Доказательство. Т.к. функции и непрерывны в точке , то ,

. Тогда ,

, . Следовательно, функции

и непрерывны в точке . Теорема доказана.

Функция называется непрерывной на сегменте , если она непрерывна в каждой точке и непрерывна в точке справа и в точке слева, т.е.

Функция называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала.

Классификация точек разрыва.

Точка называется точкой разрыва функции , если функция в точке не является непрерывной

Точка называется точкой устранимого разрыва функции , если в точке существуют равные односторонние пределы, но эти пределы не равны значению функции в точке , т.е.

Точка называется точкой разрыва первого рода функции , если в этой точке существуют не равные конечные односторонние пределы, т.е.

Точка называется точкой разрыва второго рода функции , если хотя бы один из двух односторонних пределов функции в этой точке, либо не существует, либо является бесконечным.

28 Билет

Основные свойства непрерывных функций.

Теорема 5.2. (теорема об устойчивости знака непрерывной функции). Пусть функция непрерывна в точке и . Тогда существует положительное число такое, что всюду в –окрестности точки , функция имеет тот же знак, что .

Доказательство. Приведем доказательство теоремы для случая Случай рассматривается аналогично. Т.к., функция непрерывна в точке , то для положительного числа , что для всех , удовлетворяющих неравенству

будет выполняться неравенство или

.

Из левого неравенства следует, что в каждой точке , из –окрестности точки , справедливо неравенство . Теорема доказана.

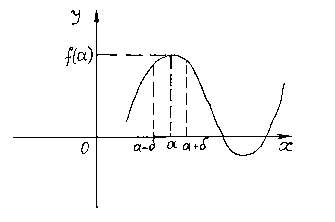
Аналогичная теорема справедлива и для функции, которая является непрерывной в точке только справа или только слева.

Для любого полусегмент будем называть правой -полуокрестностью точки , а полусегмент – левой -полуокрестностью точки .

Справедлива следующая теорема.

Теорема 5.3. (О прохождении через нуль непрерывной на сегменте функции) Пусть функция непрерывна на сегменте и её значения на концах этого сегмента и являются числами разных знаков, тогда внутри сегмента найдётся такая точка , что .

Доказательство. Без ограничения общности можно считать, что . Обозначим через . Это множество не является пустым, т.к. . Кроме этого множество ограничено сверху, т.к. для каждой точки . В силу теоремы 2.1 §2 гл. 5 у множества существует точная верхняя грань. Обозначим . Заметим, что не может совпадать с концами сегмента ибо из условий , , ,из непрерывности функции в точке справа, и в точке слева и из то из теоремы 5.2 следует, что существует правая точки , в пределах которой , и левая точки в пределах которой

Докажем, что . Предположим обратное. Пусть . Тогда либо .

Если , то в силу теоремы 5.2 существует окрестность точки всюду в пределах которого . Следовательно, существует такая точка , что , чего быть не может, так как является точной верхней гранью множества точек, в которых значение функции меньше ноля.

Если , то в силу теоремы 5.2 существует окрестность точки всюду в пределах которого . Из определения точной верхней грани следует, что для числа существует точка , множества . Тогда с одной стороны так как С другой стороны , так как в каждой точке интервала . Получаем противоречие, что вызвано предположением . Теорема доказана.

Теорема 5.4. (прохождение непрерывной на сегменте функции через любое промежуточное значение) Пусть функция непрерывна на сегменте , причём . Тогда для любого значения , заключённого между и , на сегменте найдётся точка , такая что .

Доказательство. Могут представиться два случая:

. Для этого случая теорема очевидна, так как в качестве точки можно взять точку или .

Число совпадает с одним из чисел и . Для этого случая теорема очевидна, так как в этом случае, в качестве точки можно взять соответственно, либо либо

. Без ограничения общности, будем считать, что . Пусть - любое число, удовлетворяющее неравенству . Рассмотрим функцию . Очевидно, функция непрерывна на сегменте . Кроме этого и

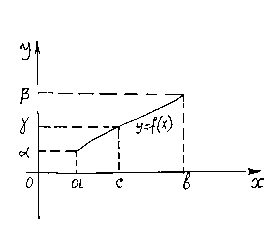
. Тогда, согласно теореме 5.3, существует такая точка внутри сегмента, что . Следовательно, . Теорема 5.4 доказана.

Вспомним, что называется ограниченной на отрезке , если существует положительное число , такое, что для всех справедливо неравенство , или

Функция называется ограниченной сверху на отрезке , если существует такое число , что .

Функция называется ограниченной снизу на отрезке , если существует такое число , что справедливо неравенство .

Из сказанного выше следует, что функция ограничена на отрезке тогда и только тогда, когда она ограничена и сверху и снизу на отрезке .

Сформулируем теперь следующую теорему.

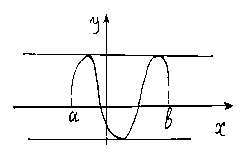
Теорема 5.5. (Первая теорема Вейерштрасса) Если функция непрерывна на отрезке , то она ограничена на этом сегменте.

Доказательство. Нам нужно доказать ограниченность функции на отрезке . Приведём доказательство только ограниченности сверху, ибо ограниченность снизу доказывается аналогично.

Доказательство будем проводить от противного. Пусть функция не ограничена сверху на сегменте .

Для каждого натурального рассмотрим множество . По предположению функция не ограничена на , поэтому для любого натурального .

Очевидно, - ограниченное множество. Тогда, силу теоремы 2.1, у каждого множества существует точная нижняя грань. Обозначим точную нижнюю грань множества через .

Заметим также, что для каждого Действительно. Если . Следовательно

Итак, мы имеем последовательность непустых, ограниченных множеств . Из теоремы 2.1 §2 главы 5 следует, что для любого у множества существует точная нижняя грань .

Рассмотрим последовательность . Последовательность удовлетворяет следующим трем условиям:

Последовательность ограничена сверху;

неубывающая последовательность;

.

Ограниченность сверху последовательности следует из того факта, что для любого .

Для любого . В силу теоремы 2.2 главы 5 . Следовательно, неубывающая последовательность.

Докажем теперь, справедливость третьего условия. Предположим, что . Тогда значение непрерывной функции в точке , меньше ноля. В силу теоремы 5.2., существует такая окрестность , всюду, в пределах которой , т.е. . С другой стороны, из определения точной нижней грани, следует существование такой точки , для которой справедливы неравенства Но тогда , что противоречит условию . Следовательно, для любого .

Итак, - неубывающая, ограниченная последовательность. В силу теоремы 3.10. последовательность сходится.

Пусть - предел последовательности . Согласно теореме 3.8. точка принадлежит сегменту . Следовательно, функция непрерывна в этой точке. Тогда, последовательность должна сходиться к значению , чего быть не может, так как

Полученное противоречье вызвано предположением о неограниченности функции

Теорема 5.5 доказана.

Замечание. В теореме 5.5 требуется, чтобы функция была определена на сегменте . Это требование является существенным.

Рассмотрим функцию . Очевидно, эта функция непрерывна, но не ограничена на интервале Т.е. из непрерывности функции на интервале не следует её ограниченность на этом интервале.

Из теоремы 5.5 следует, что множество значений непрерывной на сегменте функции является ограниченным множеством. Согласно теореме 2.1 §2 главы 5 у этого множества существуют точная верхняя и точная нижняя грани . Числа и называются соответственно точной верхней и точной нижней гранями функции на сегменте и обозначаются символами , .

Естественно возникает вопрос: являются ли для непрерывной на сегменте функции эти точные грани достижимыми, т.е. существуют ли такие точки и , принадлежащие сегменту , что и . Ответ на этот вопрос дает следующая теорема.

Теорема 5.6. (Вторая теорема Вейерштрасса). Если функция непрерывна на сегменте , то она достигает на этом сегменте своих точных граней, т.е. существуют точки , сегмента такие, что

Доказательство. Рассмотрим случай точной верхней грани (случай точной нижней грани рассматривается аналогично). Т.к. функция непрерывна на сегменте , то по теореме 5.5 она ограничена на этом сегменте Пусть .

Покажем, что существует точка такая, что . Предположим обратное, т.е. . Тогда . Рассмотрим на сегменте функцию . По теореме 5.1 §5 главы 5 функция непрерывна на сегменте . Из теоремы 5.5 следует ограниченность функции на этом сегменте, т.е. , такое что

тогда . Таким образом число является верхней гранью функции на сегменте . Но это противоречит тому, что число является точной верхней, гранью функции на отрезке . Это противоречие вызвано предположением о том, что функция не принимает значение ни в какой точке