24 Билет

Арифметические операции над функциями, имеющими предел.

Теорема 4.2. Пусть функции и имеют в точке пределы и эти пределы соответственно равны и . Тогда функции ,

имеют в точке пределы, равные соответственно Если кроме этого, , то в точке существует предел функции равный .

Доказательство. Пусть - произвольная сходящаяся к последовательность значений аргумента, элементы которой отличны от . Тогда последовательности и сходятся соответственно к пределам и . Но тогда, в силу теоремы 3.7, последовательности

и (при ) имеют пределы, соответственно равные и . Последнее утверждение, в силу определения предела функции по Гейне, означает, что , , . Теорема 4.2 доказана.

Теорема 4.3. Пусть функции и определены в некоторой окрестности точки , за исключением, быть может, самой точки и имеют в этой точке равные пределы. Пусть кроме этого выполняются неравенства . Тогда существует при этом .

Доказательство. Пусть - произвольная, сходящаяся к последовательность, элементы которой отличны от . Тогда соответствующие последовательности и имеют предел, и эти пределы равны. Из условия теоремы следует, что . Тогда согласно теореме 3.9 Следовательно, существует и и при этом . Теорема 4.3 доказана

Пусть f(x) и g(x) имеют пределы в точке а и они соответственно равны В и С.

f(x) +g(x), f(x) - g(x), f(x)g(x) имеют в точке а придел при этом,

lim(x->a)( f(x) +g(x), f(x) - g(x)) = B+-C

Предел произведения будет равнятся произведению ВС

Если С не равняется 0, то существует предел отношения,

ктр будет равнятся отношению В к С

25 Билет

Теорема 3.8. (о предельном переходе в неравенствах). Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству

, то и предел этой последовательности удовлетворяет неравенству .

Доказательство. Пусть все элементы , начиная с некоторого номера, удовлетворяют неравенству . Докажем, что . Предположим обратное, т.е. . Рассмотрим положительное число . Для этого числа существует номер такой, что для всех верно неравенство . Раскрывая модуль, получим . Из правого неравенства следует .

Последнее неравенство противоречит условию теоремы. Теорема 3.8 доказана.

Следствие 1. Если элементы сходящихся последовательностей и , начиная с некоторого номера, удовлетворяют неравенству , то их пределы удовлетворяют неравенству

Действительно, рассмотрим последовательность . Из условия имеем, что начиная с некоторого номера, члены последовательности неотрицательны, т.е. . Тогда из теоремы 3.8 следует, что . Т.е. .

26 Билет

Первый замечательный предел. Докажем справедливость равенства

Рассмотрим окружность радиуса 1, с центром в начале координат. Обозначим радиальную меру угла через .

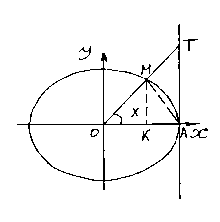
Тогда . Очевидно, что площадь меньше площади сектора , которая меньше площади . Т.к. ,

, то . Учитывая равенства (8) в последних неравенствах, найдём

.

Разделив обе части неравенств (9) на ,получим

или .

Из неравенств (10) находим

.

Т.к., , то , поэтому из неравенств (11) имеем

.

Из неравенств (12) и теоремы (4.3) следует

Из последнего равенства следует справедливость равенство (7).

Второй замечательный предел. . Ранее мы доказали, что

.

Третий замечательный предел. Докажем, что . Действительно

. Пусть . Тогда при . Поэтому . Тогда .

Четвёртый замечательный предел. Докажем, что .

Очевидно, что если , то равенство (14) выполнено. Пусть и .

Введем обозначение = . Тогда при . При этом, .

Пятый замечательный предел. Докажем, что .Пользуясь основным логарифмическим тождеством, представим в виде . Обозначим . Тогда при .

Из равенства (14) имеем и . Т.е.