§4. Системы с верхней трапециевидной матрицей.

Рассмотрим систему линейных алгебраических уравнений с верхней трапециевидной матрицей

Возможны следующие четыре случая.

Случай 1. Пусть матрица имеет вид

В случае 1 система (1) имеет вид

При этом расширенная матрица системы (2) имеет вид

.

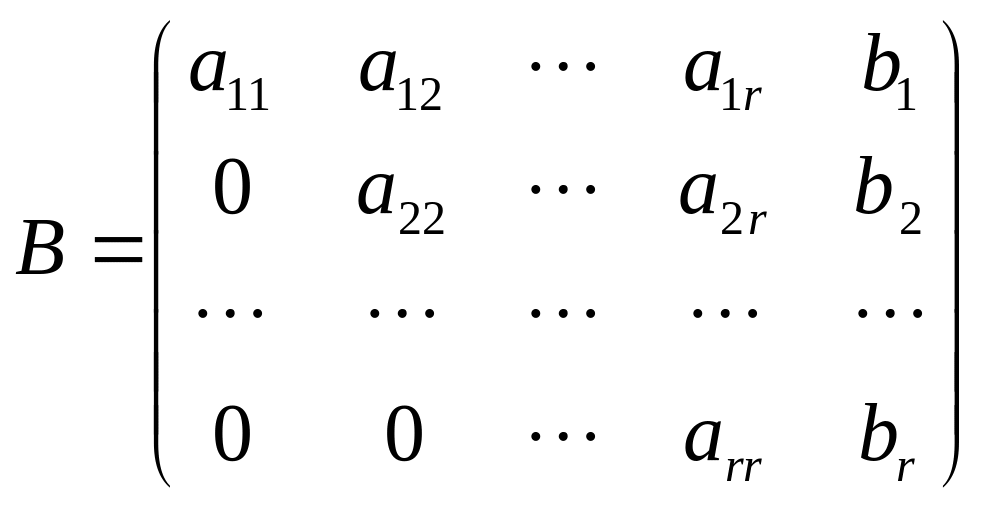Легко заметить, что .

Найти решение системы (2) не представляет труда: решая последовательно уравнения системы снизу вверх, мы каждый раз будем иметь дело с уравнением, содержащим только одно неизвестное.

Заметим, что в случае 1 система (2), а стало быть и система (1) имеет единственное решение.

Случай 2. Пусть матрица имеет вид

В случае 2 система (1) имеет вид

А расширенная матрица - вид

.

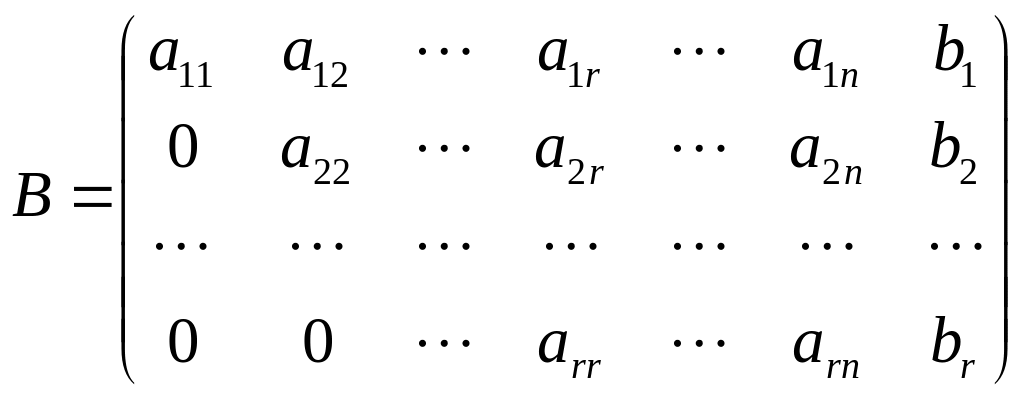Как и в случае (1), .

Назовём неизвестные – главными неизвестными, а – свободными.

Перенося в уравнениях системы (3) все слагаемые, содержащие свободные неизвестные в правую часть, получим

Решая последовательно уравнения системы (4) снизу вверх, мы получим выражения главных неизвестных через свободные - . Указанные выражения неизвестных через неизвестные называется общим решением системы (1).

Придавая свободным неизвестным произвольные числовые значения , вычислим соответствующие значения главных неизвестных. Пусть эти значения .

Очевидно, что упорядоченный набор является решением системы (3). Это решение называется частным решением.

Так как свободным неизвестным можно придать бесконечное множество значений, то и система (3) имеет бесконечное множество решений.

Следовательно, система (1), в случае имеет бесконечное множество решений.

Случай 3. Пусть матрица имеет вид

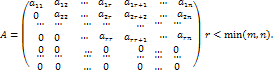
Тогда система (1) имеет следующий вид

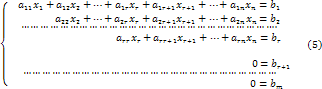
Докажем, что система (5) совместна тогда и только тогда, когда .

Доказательство. Пусть система (5) совместна. Тогда существуют такие значения неизвестных , при которых все уравнения системы превращаются в тождества. Следовательно . Пусть теперь выполнены равенства . Тогда система (5) имеет вид

Система (6) называется укороченной системой. Очевидно, что, при выполнении равенств

системы (5) и (6) эквивалентны.

Основная матрица системы (6) имеет вид, рассмотренный в случае 2. Следовательно, система (6) имеет бесконечное множество решений, а стало быть, совместна.

Заметим, что в случае 3, при выполнении равенств , расширенная матрица

системы (5) является верхней трапециевидной матрицей, при этом

Таким образом, в случае , если среди коэффициентов хотя бы один не равен нулю, то система (5) несовместна. Если же все , то система (5) имеет бесконечное множество решений.

Случай 4. Пусть верхняя трапециевидная матрица имеет вид

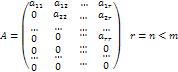
Тогда система (1) имеет вид

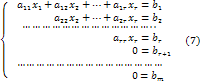
Из чего следует, что система (7) совместна тогда и только тогда, когда все . При этом, если все , то система (7) эквивалентна укороченной системе (2), описанной в случае 1, которая имеет единственное решение.

Заметим, что в случаях 3 и 4, равенство выполняется тогда и только тогда, когда . Следовательно, как и в случаях 1 и 2, система (1) совместна тогда и только тогда, когда

Из проведённых выше рассуждений следует, что система линейных алгебраических уравнений с верхней трапециевидной матрицей совместна тогда и только тогда, когда ранг основной матрицы При этом система либо имеет единственное решение ( , либо имеет бесконечное множество решений ( , либо не имеет ни одного решения (