49 Билет
Существование первообразной у любой непрерывной функции.
В данном
параграфе мы будем рассматривать
интеграл вида 
,
где подынтегральная функция
определена и интегрируема на некотором
сегменте
,
а
- произвольная точка сегмента
.
Определим
на сегмента
функцию
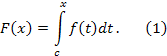
теорема 3.1. Пусть функция непрерывна на сегменте , тогда функция , определённая равенством (1), дифференцируема в каждой точке x сегмента , при этом
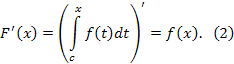
Доказательство. Пусть x произвольная точка сегмента . Тогда
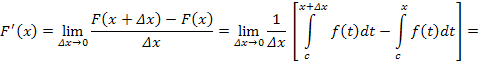
Согласно формуле среднего значения
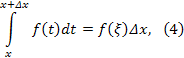где
Учитывая равенство (4) в равенстве (3), получим
Пользуясь
непрерывностью функции
в точке
и тем, что 
,
из равенства (5) получим, 
.
Теорема 1.1 доказана.
Замечание.
Из
теоремы 3.1 следует, что для непрерывной
на сегменте
функции
функция
является одной из первообразных. Тогда,
в силу следствия из теоремы 1.1, гл.8, любая
первообразная функции
будет иметь вид 
.
§4. Основная формула интегрального исчисления.
1. Формула Ньютона-Лейбница.
Пусть
функция
непрерывна на сегменте
,
тогда, в силу теоремы 3.1 для любой точки
,
функция
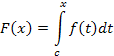
является
одной из первообразных функции
.
В частности, взяв в качестве точки
точку
,
получим, что и функция 
является первообразной функции
.
Теорема 4.1. Пусть функция непрерывна на сегменте и - любая первообразная функции на этом сегменте, тогда
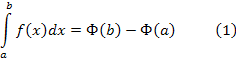
Доказательство. Так как является одной из первообразных функции на сегменте , то, в силу теоремы 1.1 главы 8, первообразную функцию можно представить в виде
где
- некоторая постоянная. Пользуясь
равенством (2), вычислим 
.
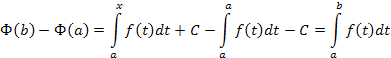
Тем самым справедливость формулы (1) доказана.
Формула (1) называется формулой Ньютона-Лейбница.
Пользуясь обозначением
формулу Ньютона-Лейбница можно записать в виде
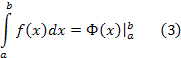
2. Замена переменной в определённом интеграле.
Теорема
4.2.
Пусть
функция
непрерывна на сегменте
,
а функция
дифференцируема на сегменте
,
причём производная
непрерывна в каждой точке сегмента
.
Пусть множеством значений функции 
является сегмент
и при этом 
,
тогда справедлива формула
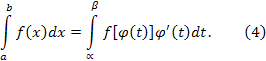
Доказательство. Пусть F(x) – какая-нибудь первообразная функции на сегменте ; тогда по формуле Ньютона-Лейбница
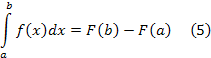
Рассмотрим
функцию 
,
определённую на сегменте
.
Согласно правилу дифференцирования
сложной функции
Отсюда
следует, что функция 
является первообразной для функции
,
непрерывной на сегменте
,
и поэтому, согласно формулк Ньютона-Лейбница,
получим
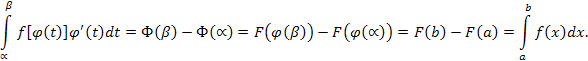
Теорема доказана.
3. Формула интегрирования по частям в определённом интеграле.
Теорема
4.3.
Пусть функции
и 
имеют непрерывные производные на отрезке
,
тогда справедлива формула
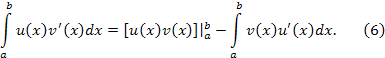
Доказательство.
Так как функция
является первообразной для функции 
,
то, согласно формуле Ньютона-Лейбница
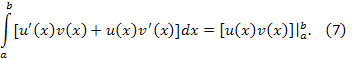
Из равенства (7) найдём
Теорема 4.3 доказана.
Учитывая
справедливость равенств 
формулу (6) можно записать в более
компактной форме:
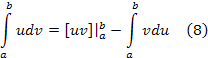
50 Билет
Несобственный интеграл первого рода.
Пусть
функция
определена на множестве 
и интегрируема на любом сегменте 
.
Тогда, если
существует конечный предел
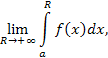
то этот предел называется несобственным интегралом первого рода и обозначается символом
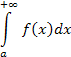
Таким образом, по определению
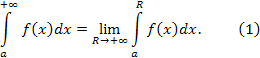
В случае,
когда существует конечный предел 
,
интеграл 
называется сходящимся, в противном
случае расходящимся.
Аналогично
интегралу (1) вводится несобственный
интеграл по промежутку 
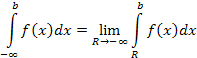
Наконец, несобственный интеграл с двумя бесконечными пределами
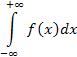
определяется
как сумма двух несобственных интегралов
и 
,
где
– любое действительное число, при
условии существования обоих несобственных
интегралов, т.е.
В качестве примера вычислим несобственный интеграл
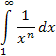
Рассмотрим два случая.
1) 
.
Пользуясь определением несобственного
интеграла I
рода,
2) Если
,
легко убедиться, что 
расходится. Следовательно, 
сходится при 
и расходится при 
.