3.Ускорение при движении материальной точки по окружности

Пусть точка движется равномерно по окружности радиуса с постоянной по величине во времени скоростью. Движение точки является криволинейным. Поэтому при равномерном движении точки по окружности должно существовать нормальное ускорение, обуславливающее изменение направления скорости.

Если материальная точка за некоторый промежуток времени перемещается из положения А в положение В с изменением скорости от до , то приращение скорости за это время равно (рис. 3.5).

A v₁

∆S =∆r

R

v₁

О B D

R ∆v

C v₂

Рис. 3.5.

Перенесем вектор параллельно самому себе так, чтобы его начало совпало с точкой В. Рассмотрим треугольники АОВ и СВД. Они подобны, так как АОВ =СВД и эти треугольники являются равнобедренными (ОА=ОВ=R , ВС=ВД=. Поэтому составим пропорцию: . Отсюда . Найдем ускорение точки. Разделим обе части последнего равенства на и перейдем к пределу при . Таким образом,

(3.20)

Итак, при движении точки по окружности её нормальное ускорение зависит от скорости точки и от радиуса окружности. Оно направлено по радиусу к центру окружности и поэтому его называют центростремительным ускорением.

Для любого положения движущейся точки можно написать , где – единичный вектор нормали к круговой траектории движущейся точки, направленный к центру окружности.

Если точка движется по окружности неравномерно, то вектор скорости меняется и по величине, и по направлению. В этом случае существуют и тангенциальное и нормальное ускорения. Следовательно, полное ускорение направлено под углом к радиусу. Так как нормальное ускорение связано с изменением только направления вектора скорости, то и в случае неравномерного движения по окружности оно выражается формулой (3.20).

Рассмотрим движение точки по произвольной криволинейной траектории. Из геометрии известно, что небольшой её участок (рис.3.6) всегда можно заменить дугой окружности некоторого радиуса . Такая окружность называется кругом кривизны траектории в данной точке. Радиус его называется радиусом кривизны, величина, обратная ему, – кривизной.

ρ

ρ

ρ

Рис. 3.6.

При этом для нормального ускорения формула (3.20) сохраняется, но под радиусом окружности следует подразумевать радиус кривизны траектории. Таким образом, величина вектора полного ускорения при криволинейном движении определяется выражением:

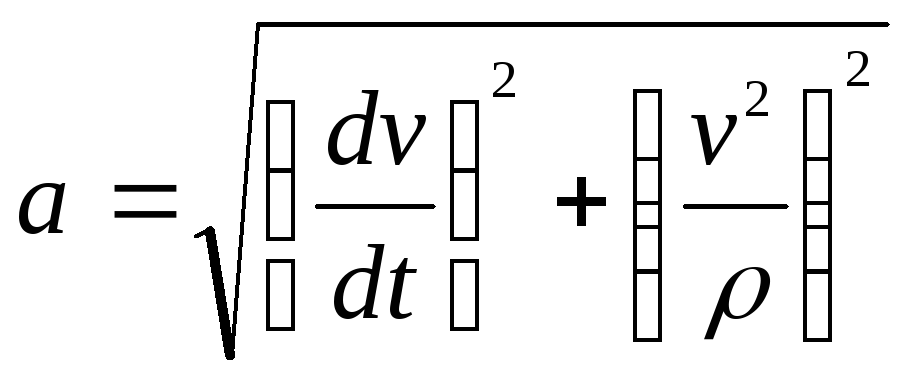(3.27)

4. Кинематика вращательного движения материальной точки

Введенные выше кинематические законы движения достаточны для описания любого вида движения материальной точки. Однако в случае вращательного движения удобнее пользоваться понятиями угловой скорости и углового ускорения.

Рассмотрим простейший случай движения материальной точки по окружности радиуса R . Выберем на окружности некоторую точку О^! в качестве начала отсчета и проведем в неё из центра окружности радиус ОО^! (рис.3.7).

O^!

А

R

А^!

φ

O

Рис. 3.7.

Положение точки А, движущейся на окружности, в некоторый момент времени можно определить при помощи угла который составляет радиус ОА, проведенный к точке с начальным радиусом ОО₁. Тогда закон движения точки может быть выражен функцией:

Пусть через некоторый промежуток времени точка оказалась в положении А₁, и угол при этом изменился на величину . Быстрота изменения угла с течением времени определяется как предел, к которому стремится отношение , если промежуток времени стремится к нулю, т.е.

(3.28)

Единицей измерения угловой скорости является радиан в секунду (рад/с или ). Рад/с – угловая скорость равномерно вращающегося тела, при которой за время 1 с совершается поворот тела относительно оси на угол 1 рад.

Угловым ускорением называют величину, характеризующую быстроту изменения угловой скорости:

(3.29)

С учетом (3.28) также имеем:

(3.30)

При малом угле поворота связь между линейным и угловым перемещением можно выразить соотношением:

Исходя из этого выражения, легко устанавливается связь между линейной скоростью v (скорость точки вдоль траектории) и угловой скоростью . Для этого достаточно разделить последнее выражение на :

Отсюда, в силу формул (3.3) и (3.28), имеем

(3.31)

Аналогично получим связь тангенциального ускорения (а не нормального!) с угловым:

(3.32)

А для определения величины нормального ускорения воспользуемся формулой : . Тогда .

Заметим, что при движении материальной точки по окружности, т.е. при вращательном движении, радиус-вектор направлен от центра по радиусу окружности , формулу для центростремительного (или нормального) ускорения можно записать в векторной форме .

Знак минус указывает на то, что направления векторов и взаимно противоположны, т.е. ускорение направлено к центру круговой траектории, по которой вращается материальная точка.

Время одного полного оборота называется периодом Т. Тогда угловая скорость , т.е. , частота .