§ 12. Вынужденные колебания

Чтобы колебания частицы в вязкой среде были гармоническими (с постоянной амплитудой ), к частице надо приложить вынужденную силу:

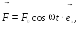
(12.1)

где положительные постоянные и ω — амплитуда и круговая частота колебаний силы соответственно.

С учетом вынуждающей силы дифференциальное уравнение (11.3) принимает вид

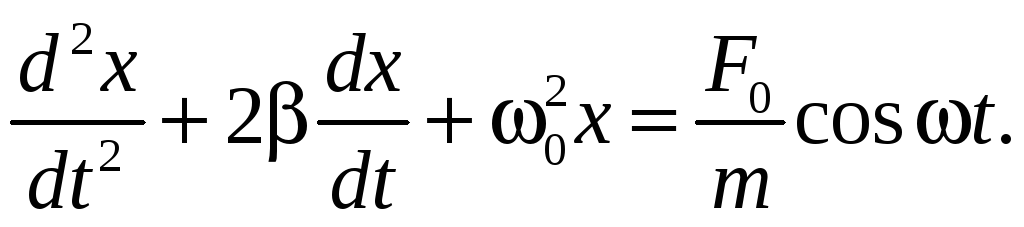(12.2)

Решение уравнения (12.2) дает закон движения частицы, называемый вынужденными колебаниями частицы,

(12.3)

где

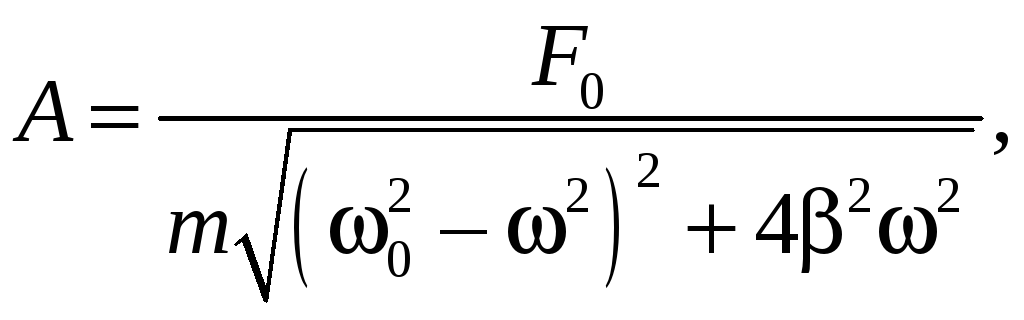(12.4)

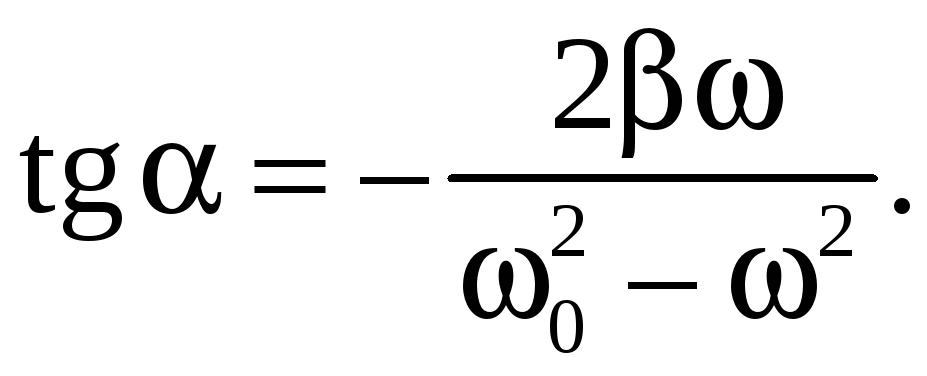(12.5)

Из выражения (12.4) видно, что амплитуда колебаний частицы зависит от круговой частоты ω колебаний вынуждающей силы . Найдем частоту при которой амплитуда имеет максимальное значение. Очевидно, что при подкоренное выражение в соотношении (12.4) должно быть минимальным, т. е. при

откуда

(12.6)

Круговую частоту называют резонансной частотой. Резкое возрастание амплитуды выраженных колебаний частицы при частоте ω колебаний вынуждающей силы равной резонансной, называют явлением резонанса.

Глава 5. Механические волны § 13. Гармонические волны

Колебания частицы, возникшие где-либо в упругой среде, будут распространяться с некоторой скоростью v в этой среде вследствие упругого взаимодействия между частицами среды. Процесс распространения колебаний частиц в упругой среде называют механической волной. Если все частицы среды при этом совершают гармонические колебания, волну называют гармонической. Отметим, что сами частицы среды не переносятся, а лишь совершают колебание около своих положений равновесия.

Назовем фронтом волны поверхность, отделяющую колеблющиеся частицы от частиц, еще не начавших колебаться. Частицы, охватываемые волновым фронтом, будут совершать колебания в одинаковой фазе или синфазно. Геометрическое место точек, где находятся положения равновесия частиц, совершающих синфазные колебания, называют волновой поверхностью. Следовательно, фронт волны — одна из волновых поверхностей. Однако в любой момент времени можно построить только один фронт бегущей волны. В то же время можно построить бесконечное множество волновых поверхностей. Фронт волны все время перемещается, а волновые поверхности остаются неподвижными, проходя через положения равновесия частиц, колеблющихся в одинаковой фазе.

Волновые поверхности могут быть любой формы. Например, они могут иметь форму плоскости или сферы. Соответственно в первом случае волну называют плоской, во втором — сферической. Волну называют продольной, если частицы среды колеблются в направлении распространения волны. Волну называют поперечной, если частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны. В однородной среде направление распространения волны перпендикулярно фронту волны.

Назовем длиной волны λ расстояние, на которое распространяется гармоническая волна за время, равное периоду колебаний частиц среды. Очевидно,

(13.1)

где v — скорость распространения волны. С учетом формулы (10.5) можем написать

(13.2)

или

(13.3)