§ 89. Электронно-дырочная проводимость полупроводников

Рассмотрим теперь более подробно поведение электронов в валентной зоне, в которой возникли свободные уровни вследствие перехода части электронов в зону проводимости (рис. 89.1).

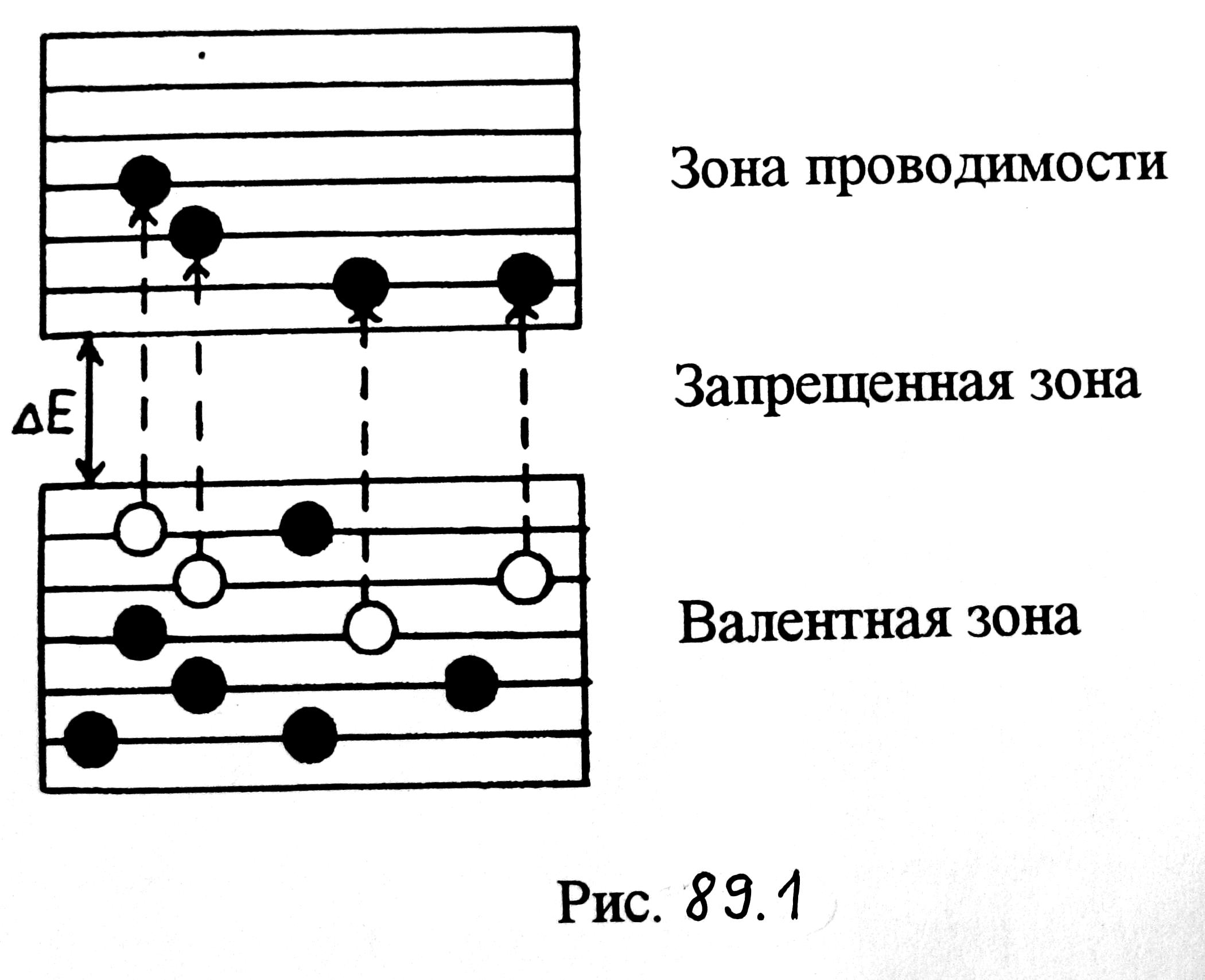
Рис. 89.1

Оказывается, что при наличии вакантных уровней в валентной зоне при включении электрического поля носителями электрического тока в этой зоне являются положительно заряженные квазичастицы, получившие названия дырок. Объясним это. Когда валентная зона полностью заполнена электронами, сумма всех их скоростей равна нулю:

Выделим из этой суммы скорости k-го электрона:

откуда

Из полученного соотношения вытекает, что если k-й электрон при нагревании кристалла переходит в зону проводимости, то сумма скоростей оставшихся электронов в валентной зоне равна . Все эти электроны создадут ток, равный . Таким образом, суммарная сила тока всех электронов валентной зоны, имеющей одно вакантное состояние, эквивалентна силе тока, обусловленного наличием в ней частицы с положительным зарядом +q, помещенной в это состояние. Такую квазичастицу называют дыркой.

Расчет дает, что количество электронов, перешедших в зону проводимости, а следовательно, и количество образовавшихся дырок пропорционально , где — ширина запрещенной зоны; k — постоянная Больцмана; T — температура. Эти электроны и дырки являются носителями тока. Поскольку электропроводимость пропорциональна числу носителей тока, можем написать

(89.1)

где σ₀ — константа. Из соотношения (89.1) видно, что удельная электрическая проводимость σ полупроводников растет с температурой T по экспоненциальному закону.

Отметим, что все вышесказанное относится к так называемым собственным полупроводникам. К ним относятся ряд чистых химических элементов (германий, кремний, селен, теллур и др.) и многие химические соединения.

§ 90. Примесные полупроводники

В ряде случаев в проводники вводят примеси для придания им необходимых электрических свойств. Примесные атомы создают свои собственные энергетические уровни, получившие название примесных уровней. Эти уровни располагаются в запрещенной зоне полупроводника на различных расстояниях от вершины валентной зоны и дна зоны проводимости. Рассмотрим основные типы примесных уровней.

Донорные уровни. Предположим, что в кристалле германия часть атомов германия заменена атомами пятивалентного мышьяка. Германий имеет решетку типа алмаза, в которой каждый атом связан ковалентными (попарно-электронными) связями с четырьмя равностоящими от него соседними атомами.

Для установления связи с этими соседними атомами германия атом мышьяка расходует четыре валентных электрона. Пятый электрон в образовании связи не участвует. Он продолжает двигаться в электрическом поле атома мышьяка, ослабленного в германии в ε = 16 раз (ε — диэлектрическая проницаемость германия), вследствие чего его энергия связи с атомом уменьшается в ε² = 256 раз, становясь равной E_д = 0,01 эВ. При сообщении электрону такой энергии он отрывается от атома и приобретает способность свободно перемещаться в решетке германия, превращаясь, таким образом, в электрон проводимости (носитель электрического тока при включении электрического поля).

На языке зонной теории процесс можно представить следующим образом. Между заполненной валентной зоной и свободной зоной проводимости располагаются энергетические уровни пятого электрона атомов мышьяка (рис. 90.1). Эти уровни размещаются непосредственно у дна зоны проводимости, отстоя от нее на расстоянии E_д = 0,01 эВ. При сообщении электронам таких примесных уровней энергии E_д они переходят в зону проводимости (рис. 90.1). Образующиеся при этом дырки локализуются на неподвижных атомах мышьяка и в электропроводности не участвуют.

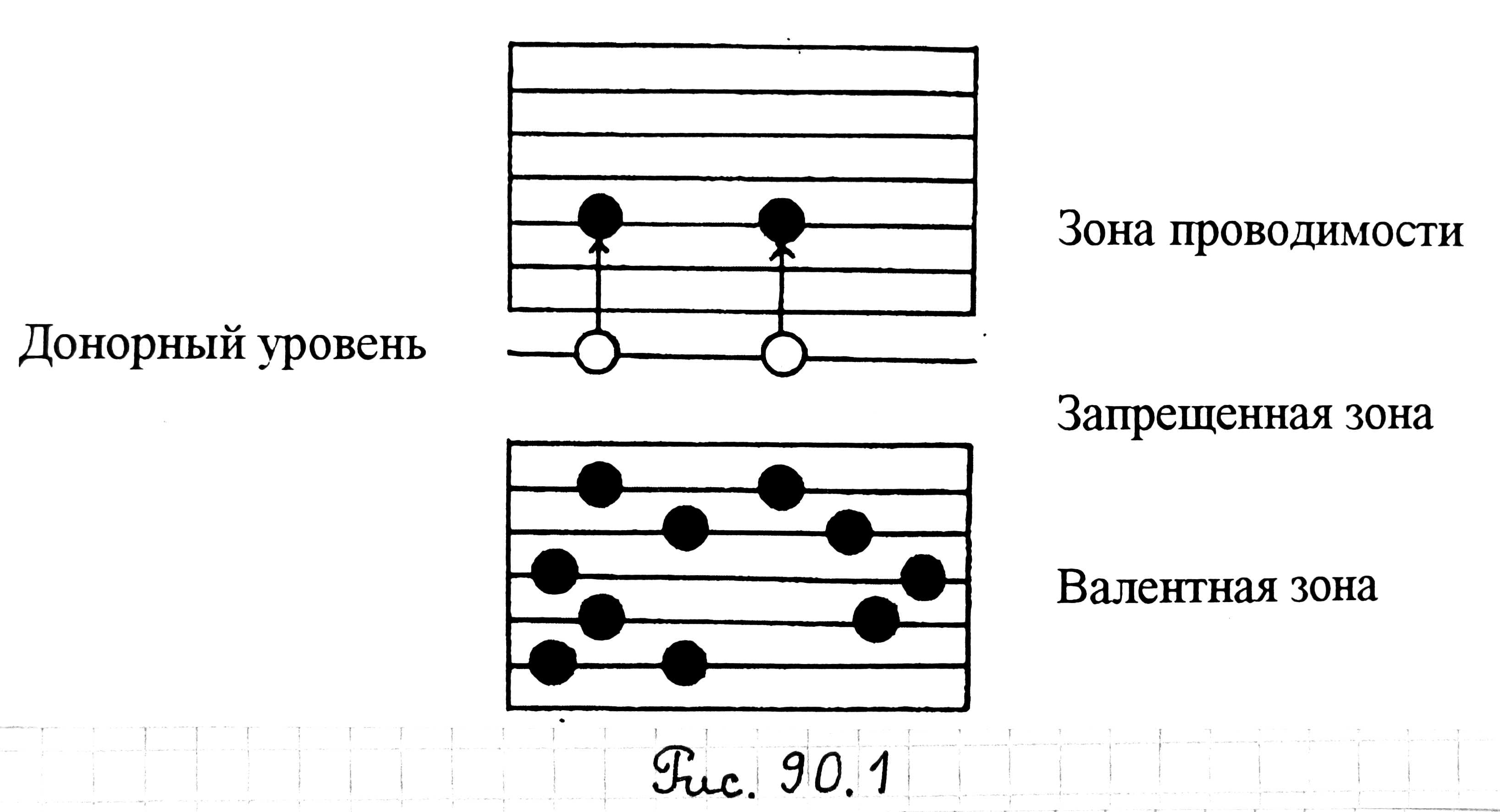
Рис. 90.1

Примеси, являющиеся источниками электронов проводимости, называют донорами, а энергетические уровни таких примесей — донорными уровнями. Полупроводники, содержащие донорную примесь, называют электронными проводниками, или полупроводниками n-типа.

Акцепторные уровни. Предположим теперь, что в решетке германия часть атомов германия замещена атомами трехвалентного индия. Для образования ковалентных связей с четырьмя соседними атомами германия у атома индия не хватает одного электрона. Для установления такой связи атом индия отбирает у атома германия один электрон из ковалентной связи соседних атомов германия. Расчет показывает, что для этого требуется энергия E_а = 0,01 эВ.

На языке зонной теории разорванная связь между соседними атомами германия представляет собой дырку, так как она отвечает образованию в валентной зоне германия вакантного состояния. Таким образом, непосредственно у вершины валентной зоны на расстоянии E_а = 0,01 эВ располагаются незаполненные примесные уровни атомов индия (рис. 90.2). При сообщении электронам валентной зоны энергии E_а = 0,01 эВ они переходят на примесные уровни (рис. 90.2). Связываясь с атомами индия, они теряют способность перемещаться в решетке германия и в электропроводимости не участвуют. Носителями электрического тока при включении электрического поля являются лишь дырки, возникающие в валентной зоне.

Зона проводимости

Запрещенная зона

Валентная зона

Акцепторный уровень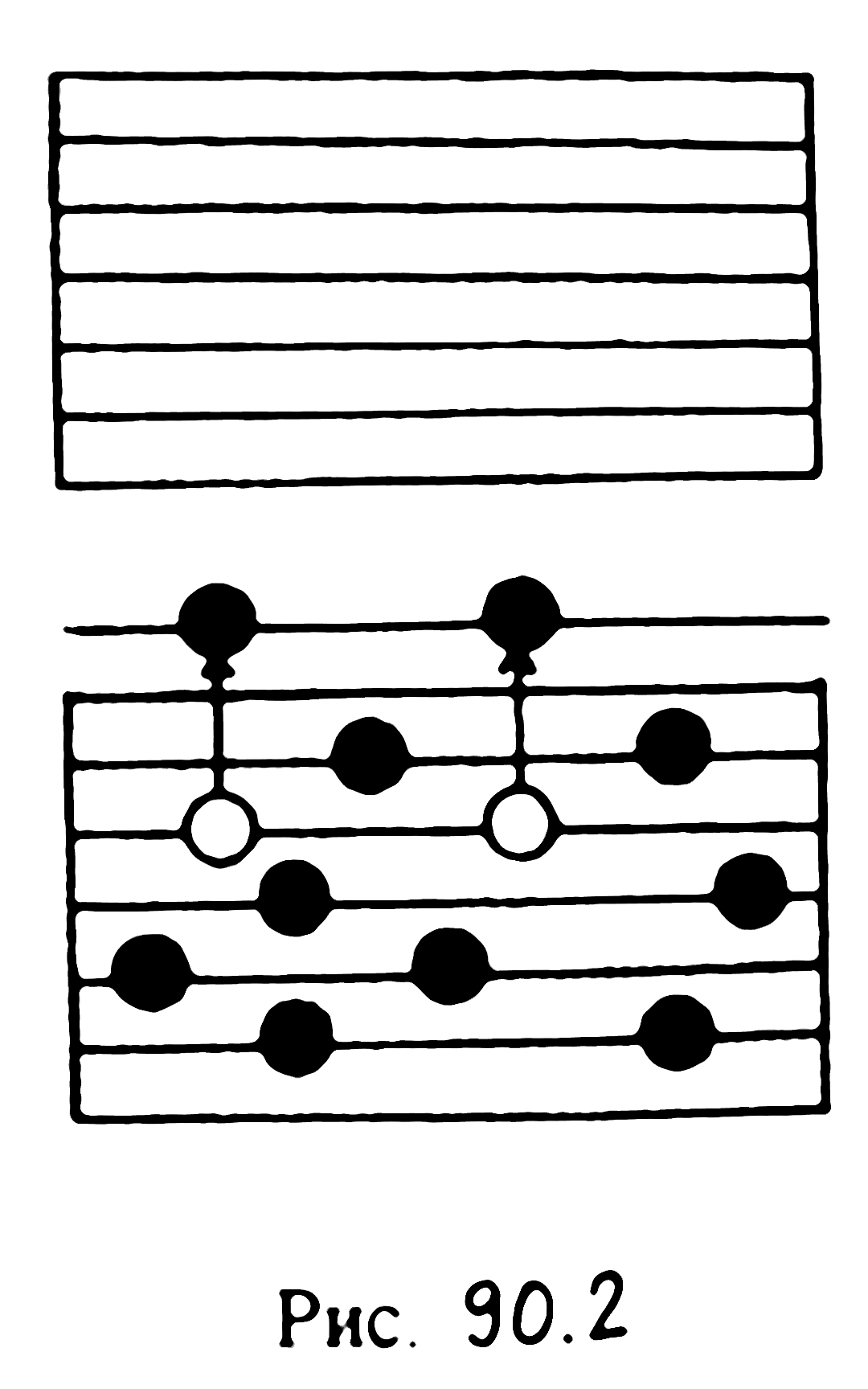

Рис. 90.2

Примеси, захватывающие электроны из валентной зоны полупроводника, называют акцепторными, а энергетические уровни этих примесей — акцепторными уровнями. Полупроводники, содержащие такие примеси, называют дырочными полупроводниками, или полупроводниками p-типа.

§ 91. p-n-переход

Полупроводники с примесной проводимостью нашли широкое применение в современной электронике.

В качестве примера рассмотрим, как действует полупроводниковый диод или выпрямитель переменного электрического тока. Основным элементом полупроводникового диода является так называемый p-n-переход. Он представляет собой тонкий слой между двумя областями одного и того же кристалла, отличающимися типом примесной проводимости (см. рис. 91.1, где слева от слоя находится область с проводимостью p-типа, а справа — n-типа).

В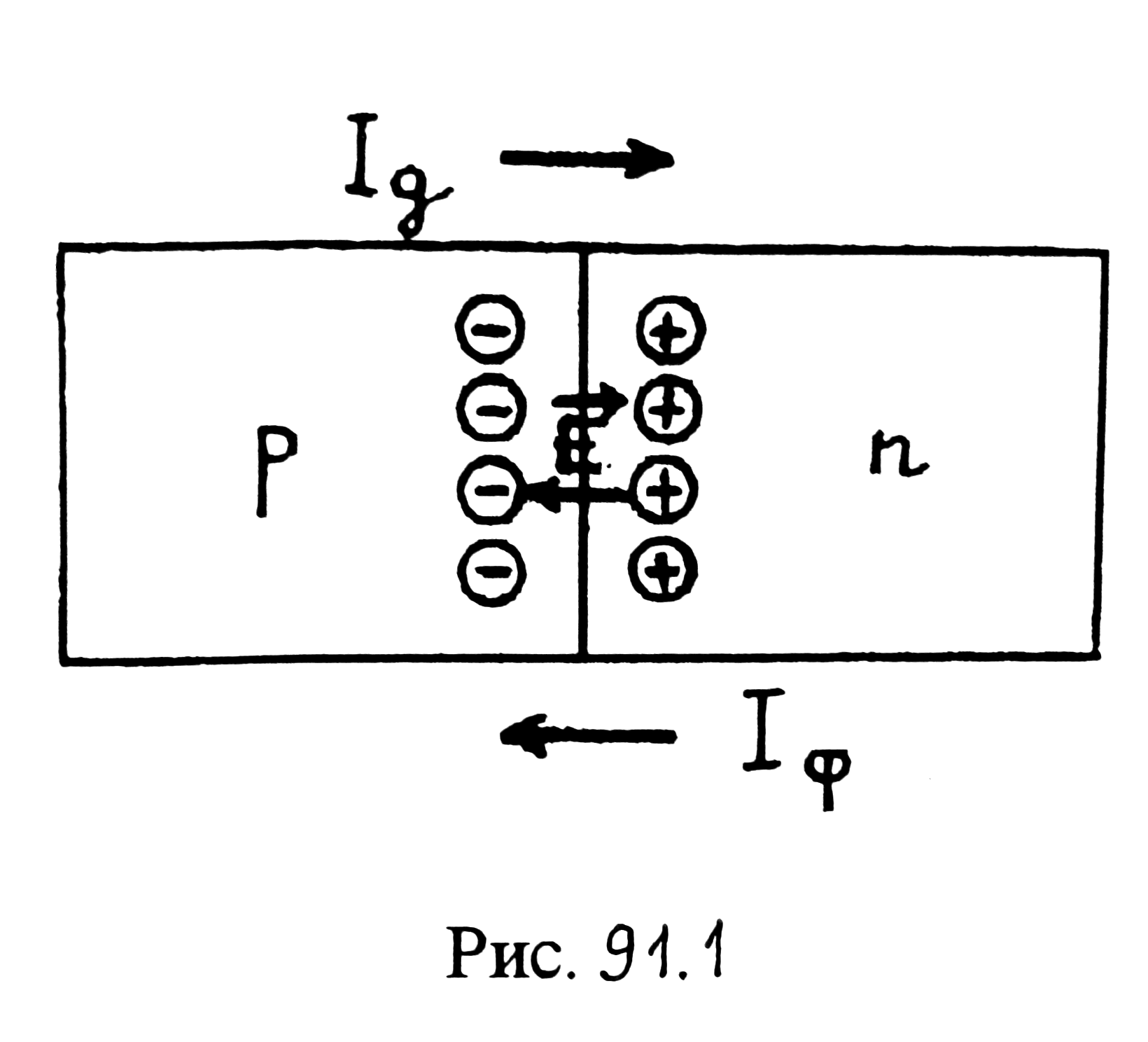 результате теплового движения свободные электроны из n-области частично проникают в p-область, а свободные дырки — из p-области в n-область. В результате возникает слабый диффузионный электрический ток I_д, текущий через p-n-переход слева направо (рис. 91.1). Электроны и дырки, попавшие в результате диффузии в «чужие» области, аннигилируют (взаимоуничтожаются) со свободными носителями тока противоположного знака. Другими словами, при встрече электрона с дыркой электрон, заполняя дырку, переходит из зоны проводимости в валентную зону — свободный электрон, так же как и свободная дырка, исчезает.

Рис. 91.1

За счет диффузного ухода части носителей тока как в n-, так и p-области возникают нескомпенсированные ионные заряды из донорных и акцепторных атомов. В n-области нескомпенсированный заряд положителен, а в p-области — отрицателен. Поэтому вблизи p-n-перехода образуется двойной электрический слой, называемый запирающим слоем. Он создает внутри перехода электрическое поле , направленное из n-области в p-область (рис. 91.1). Это поле затрудняет диффузию свободных электронов и дырок и приводит к уменьшению диффузионного тока.

Под действием тепловых флуктуаций во всем объеме кристалла время от времени рождается электрон-дырка собственного проводника (без учета примесных уровней). Появившиеся свободные электроны в p-области и свободные дырки в n-области создают слабый флуктуационный электрический ток I_ф, текущий через p-n-переход справа налево (рис. 91.1), причем I_ф = I_д.

Приложим к кристаллу с p-n-переходом внешнюю разность потенциалов. В случае, изображенном на рис. 91.2, внешнее электрическое поле будет оттягивать электроны из n-области и дырки из p-области от p-n-перехода. В этом случае единственно возможным будет только флуктуационный ток I_ф. Но он очень мал, потому что из-за тепловых флуктуаций пары электрон-дырка рождаются редко и в среднем далеко от p-n-перехода. Поэтому они обычно аннигилируются, не успев до него дойти. Следовательно, в этом случае ток через p-n-переход будет ничтожно мал.

В случае, изображенном на рис. 91.3, внешнее электрическое поле будет подгонять свободные электроны в n-области и свободные дырки в p-области к p-n-переходу. В результате резко возрастает диффузионный ток I_д.

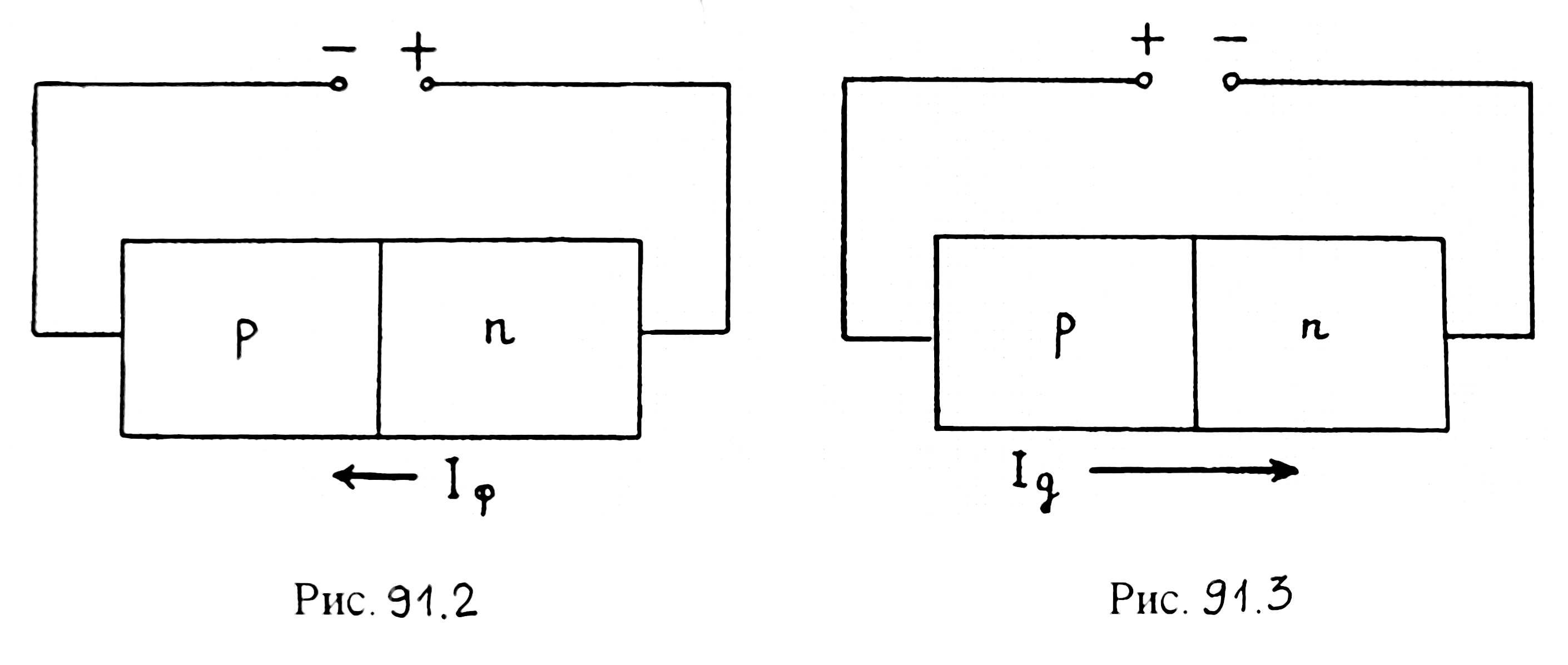
Рис. 91.2 Рис. 91.3

Мы видим, что практически у p-n-перехода есть только односторонняя проводимость. Поэтому он и может использоваться для выпрямления переменного тока. На рис. 91.4 показан график силы тока, текущего через полупроводниковый диод, в том случае если приложенное напряжение изменяется по гармоническому закону.

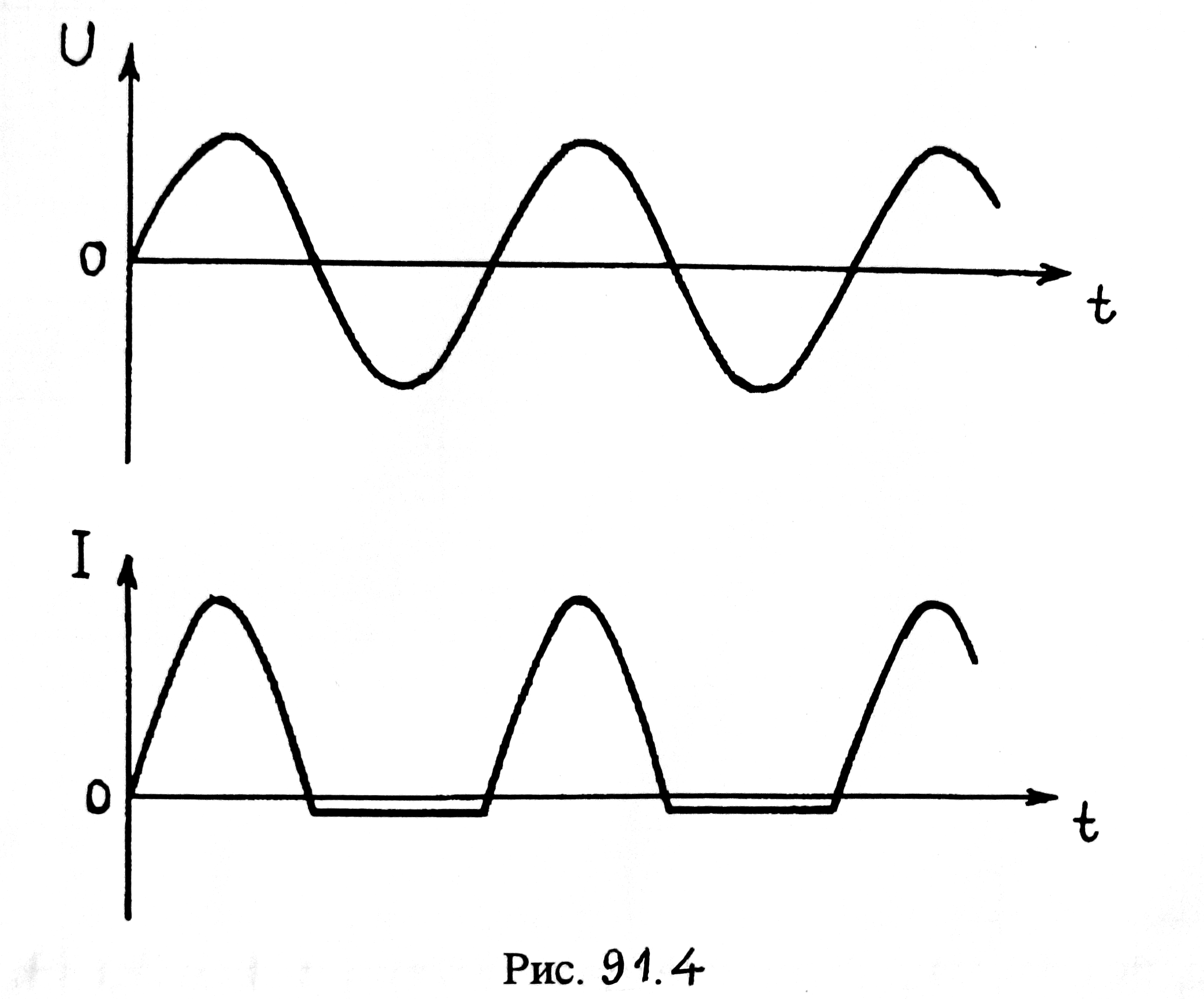
Рис. 91.4