§ 85. Излучение и поглощение света атомом водорода

Расчеты показывают, что вероятность P нахождения электрона с энергией E_n внутри атома водорода не зависит от времени и не изменяется с течением времени. Следовательно, энергетическое состояние электрона, характеризуемое определенной энергией E_n, является стационарным. Находясь в этом состоянии, электрон не излучает энергии.

Стационарное состояние атома должно сохраняться как угодно долго, если нет внешних причин, вызывающих изменение энергии атома. Однако, как показывает опыт и доказывает квантовая физика, атом, находящийся в возбужденном энергетическом состоянии E_n, сам собой переходит в более низкое энергетическое состояние E_m (спонтанное излучение). Каждый переход из состояния n в состояние m сопровождается излучением спектральной линии с частотой ν, причем

(85.1)

где hν — энергия испускаемого фотона.

При взаимодействии с электромагнитным полем атом, находящийся на уровне m, может поглотить фотон с энергией

(85.2)

и перейти в более высокое энергетическое состояние n — происходит поглощение света.

С

l = 2

l = 1

l = 0

l = 1

l = 0

l = 0

Рис. 85.1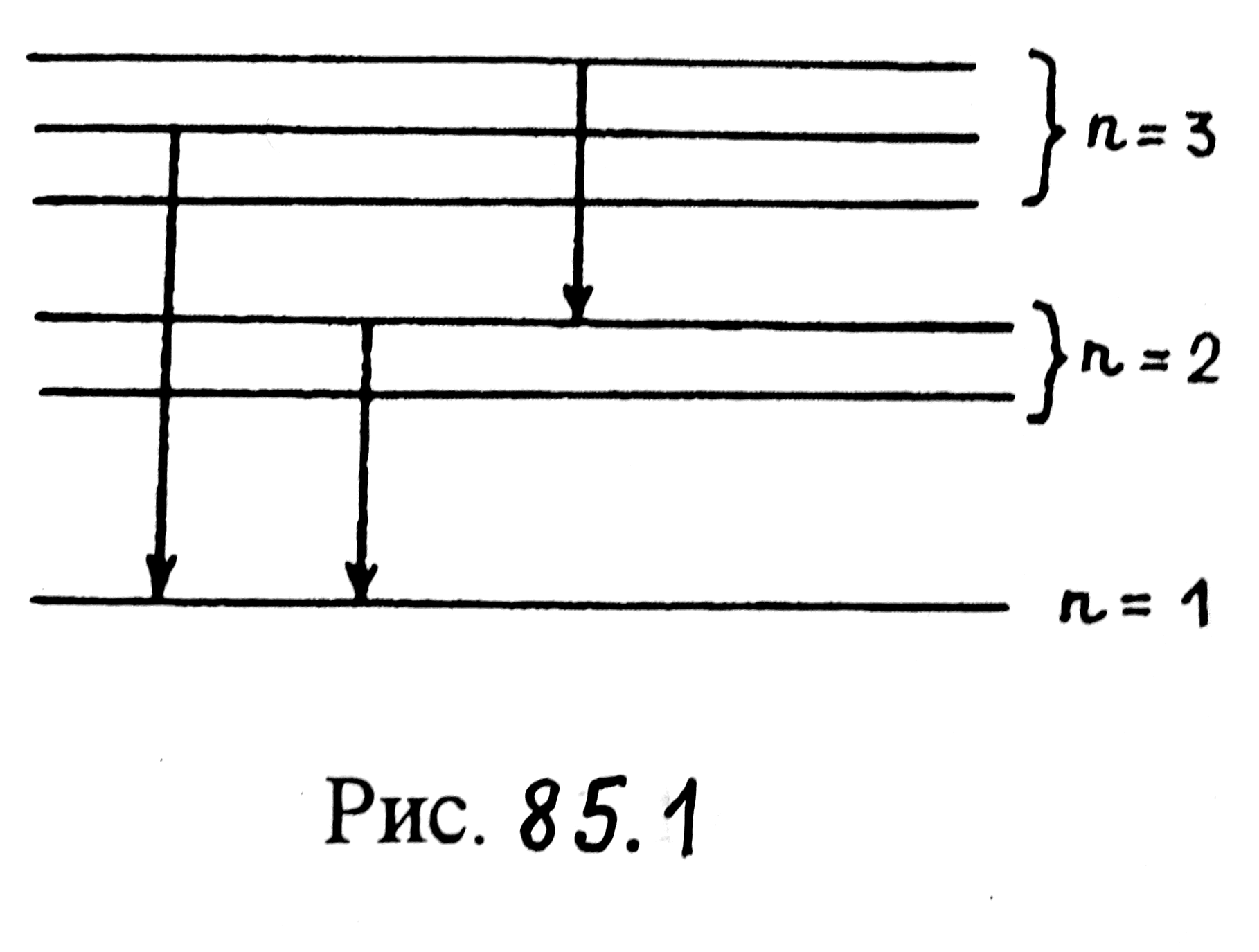

огласно выражениям (85.1) и (85.2), число линий в спектрах излучения и поглощения может быть произвольно велико. Однако это не так. Теория показывает, что существуют особые правила отбора, ограничивающие число возможных переходов электрона в атоме, связанных с испусканием и поглощением света.

Расчеты показывают, что для атома водорода энергетические переходы возможны только при изменении орбитального квантового числа на единицу: (см. рис. 85.1, на котором в виде горизонтальных линий представлены энергетические уровни, в виде вертикальных стрелок — возможные энергетические переходы в атоме водорода).

Можно определить частоту спектральных линий атома водорода по формуле

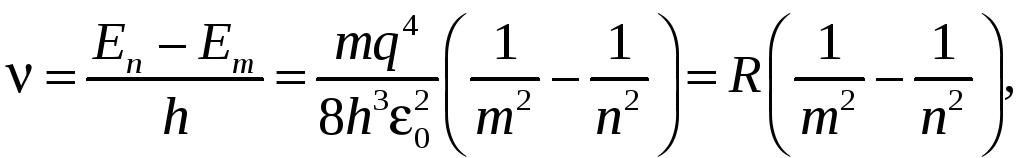(85.3)

где m и n — целые числа; R — постоянная Ридберга.

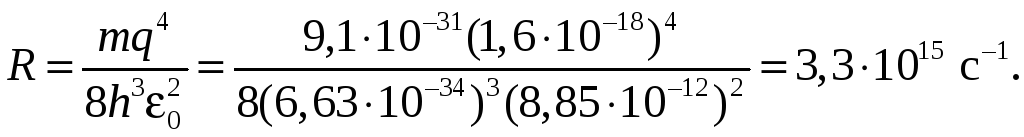
Тщательные исследования спектра атома водорода показали, что в нем наблюдается шесть серий спектральных линий:

— в ультрафиолетовой области

серия Лаймана: m = 1, n =2, 3, 4, …;

— в видимой области

серия Бальмера: m = 2, n =3, 4, 5, …;

— в инфракрасной области

серия Пашена: m = 3, n =4, 5, 6, …;

серия Брэкета: m = 4, n =5, 6, 7, …;

серия Пфунда: m = 5, n =6, 7, 8, …;

серия Хэмфри: m = 6, n =7, 9, 9, … .

Пример 85.1. Определить длину волны линии спектра испускания атома водорода, излучаемой при переходе электрона с четвертого энергетического уровня на второй.

Дано: n = 4 m = 2	Решение
λ – ?

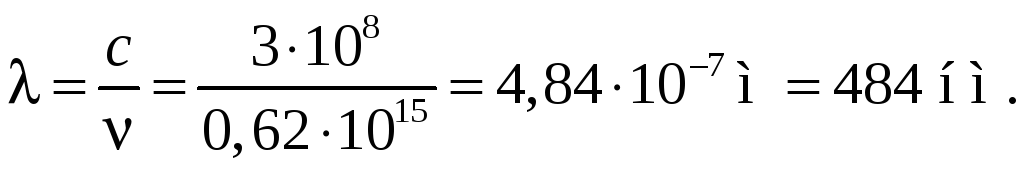
Ответ:

§ 86. Пространственное квантование

В § 84 мы установили, что модуль орбитального момента импульса электрона в атоме является квантовой величиной (см. формулу (84.2)). В квантовой механике также строго доказано, что проекция L_lz вектора орбитального момента импульса электрона на направление z внешнего магнитного поля принимает лишь целочисленные значения ћ:

(86.1)

где — магнитное квантовое число (l — орбитальное квантовое число, определяющее модуль вектора ).

Таким образом, вектор может принимать только 2l + 1 ориентаций в пространстве. Например, для электрона в p-состоянии (l = 1) возможны ориентации вектора (рис. 86.1). Для электрона в d-состоянии возможны ориентации вектора (рис. 86.2).

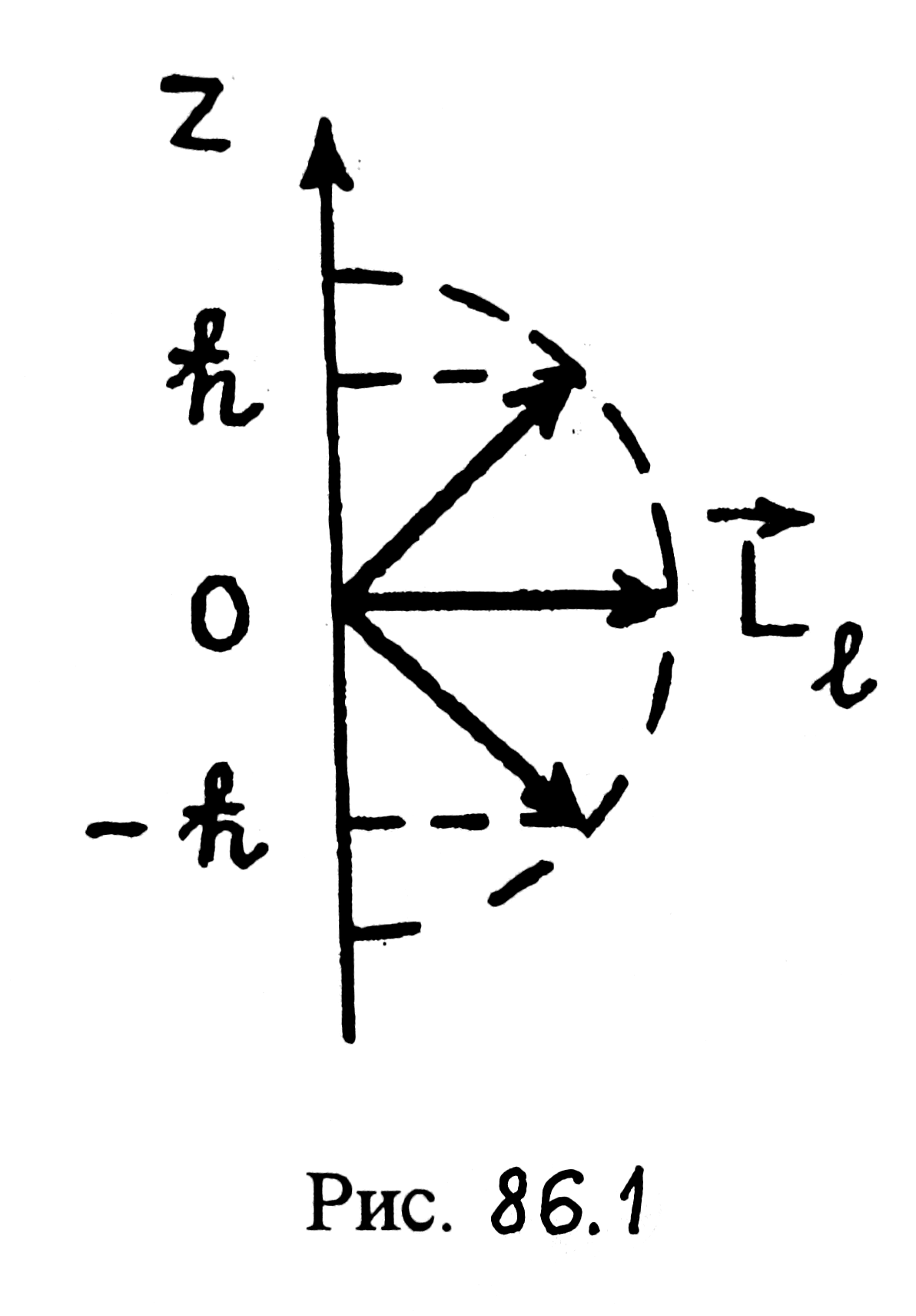
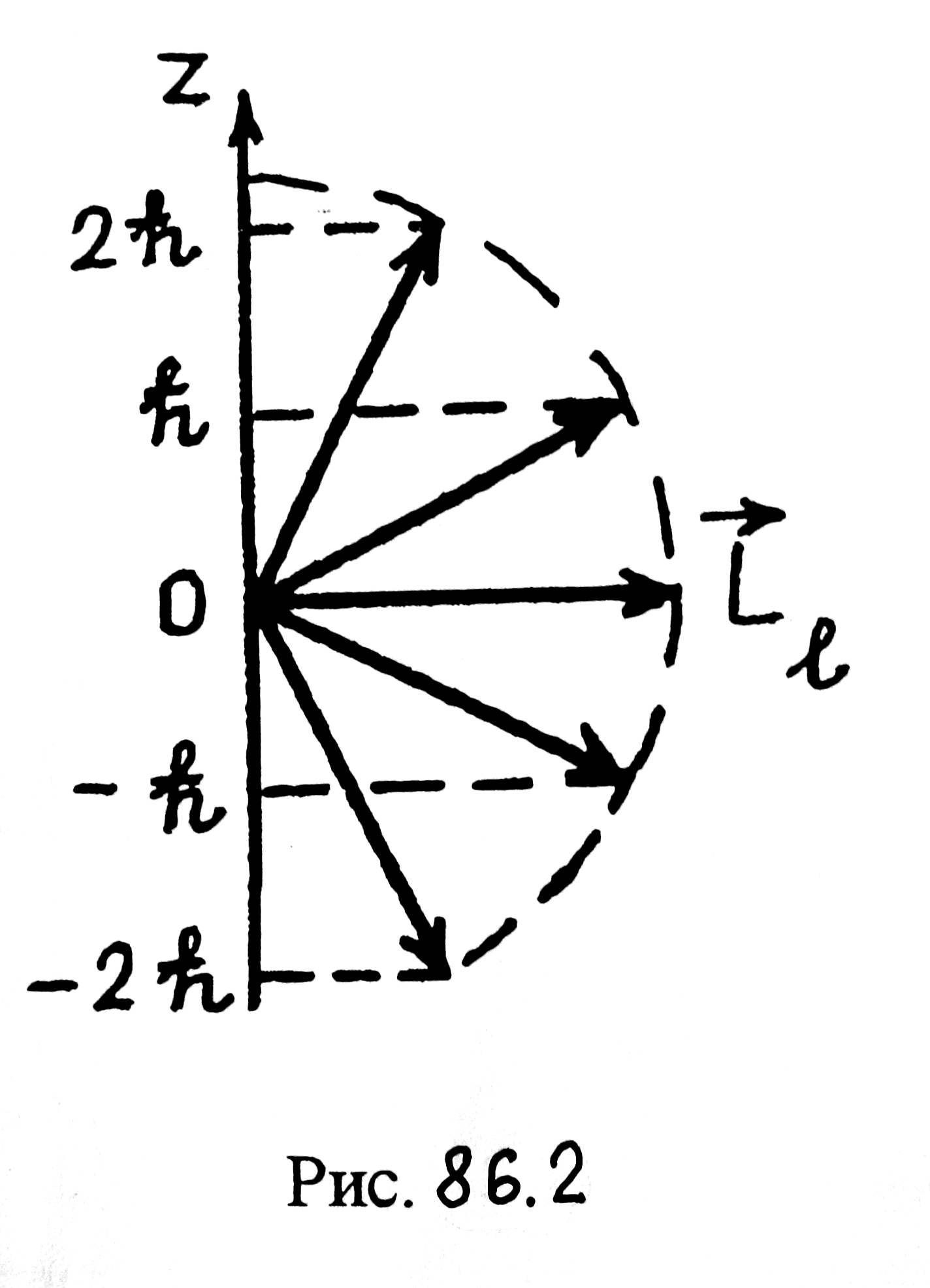
Рис. 86.1 Рис. 86.2

Дискретность возможных пространственных ориентаций момента импульса электрона относительно направления внешнего магнитного поля называют пространственным квантованием.

Пространственное квантование имеет не только орбитальный момент импульса электрона , но и собственный момент импульса электрона , называемый спином электрона. Проекция L_sz вектора спина электрона на направлении z внешнего магнитного поля принимает лишь значения согласно формуле

(86.2)

где — спиновое квантовое число. Таким образом, спин электрона имеет только две возможные ориентации во внешнем магнитном поле: по полю и против поля. Модуль электрона найдем по формуле

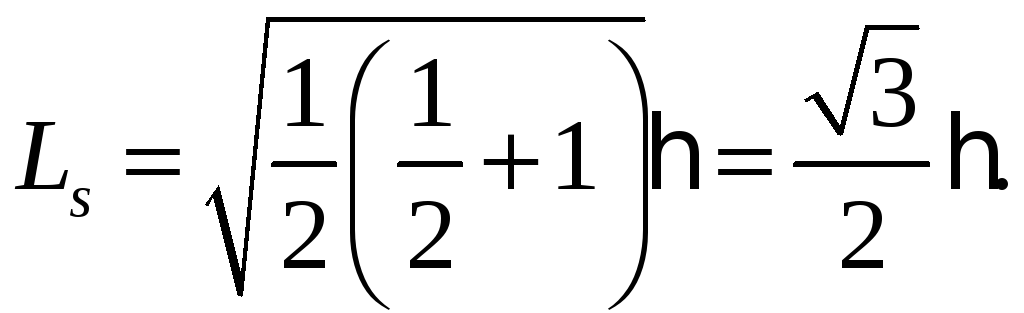(86.3)

Предположение о существовании спина было высказано в 1925 г. американскими физиками Гаудсмитом и Уленбеком. По Гаудсмиту и Уленбеку, спин электрона есть момент импульса вращающегося заряженного шарика — электрона — вокруг своей оси. Однако позднее расчеты показали, что такой шарик должен был вращаться с линейной скоростью на своей поверхности, в 200 раз превышающей скорость света в вакууме. Поэтому от такого истолкования спина отказались.

В настоящее время спин электрона и других элементарных частиц рассматривают как некоторое особое свойство этих частиц, т. е. наряду с массой и зарядом они имеют еще и спин.