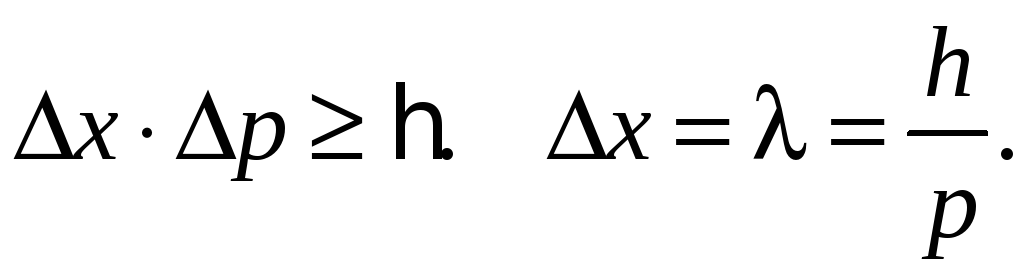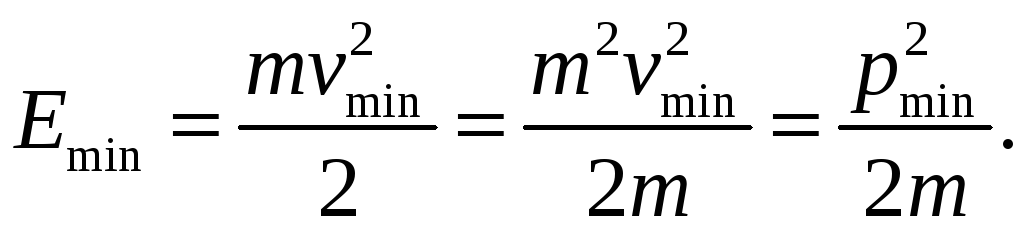- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
§ 81. Соотношение неопределенностей Гейзенберга
Е
Рис. 81.1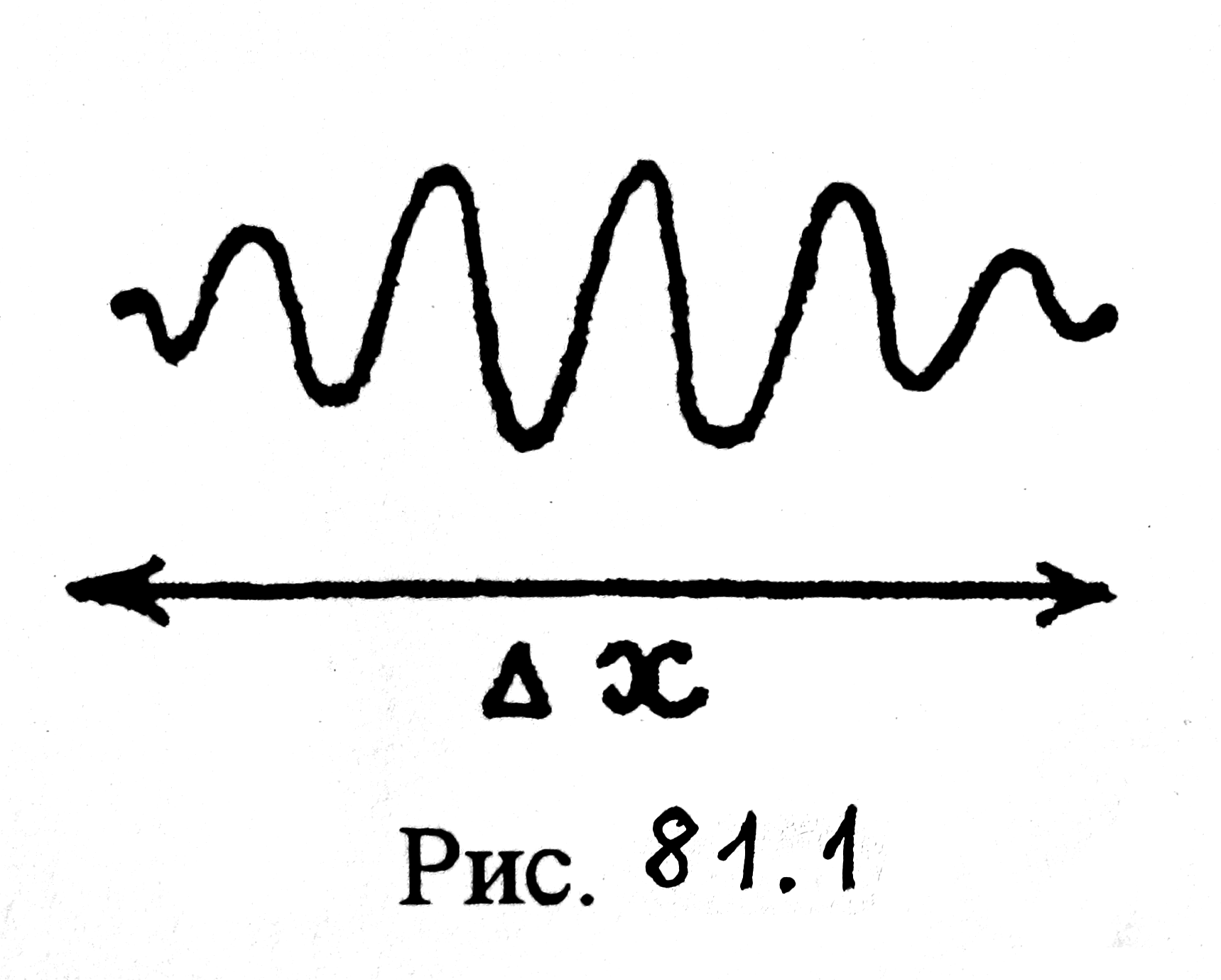
![]() (81.1)
(81.1)
Это соотношение справедливо для любых волновых процессов.
Для волны де Бройля — микрочастицы, движущейся вдоль оси x с импульсом p
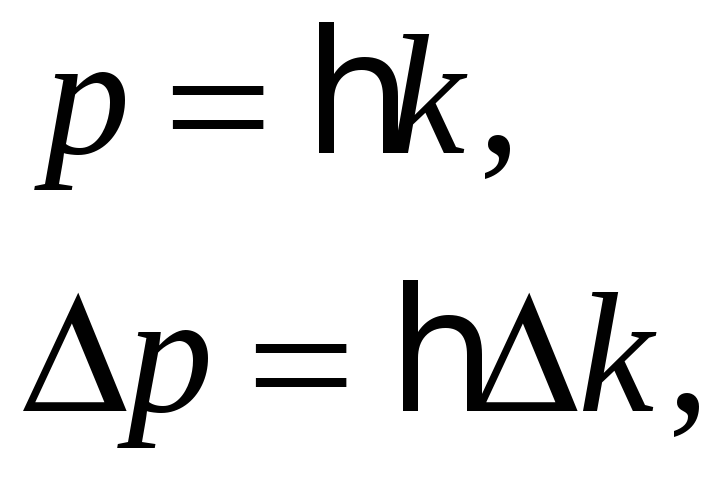
откуда
![]() (81.2)
(81.2)
Подставляя формулу (81.2) в неравенство (81.1), получаем
![]() (81.3)
(81.3)
В неравенстве (81.3) Δx — интервал координат, в котором локализована движущаяся микрочастица, описываемая волной де Бройля; Δp — интервал, в котором заключен импульс микрочастицы. Формулу (81.3) называют соотношением неопределенностей Гейзенберга. Оно показывает, что координата x микрочастицы и ее импульс p не имеют одновременно значений, равных x и p. Их значения определены лишь с некоторой степенью точности. Другими словами, классические понятия координаты и импульса применимы к микрочастицам лишь в пределах, устанавливаемых соотношением Гейзенберга (81.3).
Возникает
вопрос, почему в классической физике
соотношение (81.3) не играет никакой роли
и движущаяся макрочастица имеет
определенные значения координаты и
скорости? В качестве примера рассмотрим
пылинку массой 10–13
кг и размером 1 мкм = 10–6
м, координата которой определена с
точностью до 0,01 ее размера, т. е.
![]() .
Согласно формуле (81.3),
.
Согласно формуле (81.3),
![]()
откуда
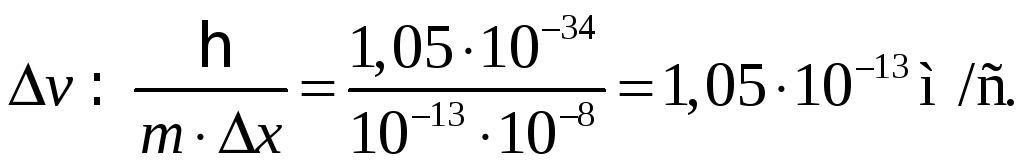
Легко сообразить, что эта неопределенность скорости практически не сказывается при всех скоростях, с которыми движется такая макрочастица. Поэтому, в отличие от квантовой механики, в классической механике применимы понятия координаты и скорости.
Пример
81.1. Определить
относительную неопределенность
![]() импульса движущейся частицы, если
неопределенность ее координаты равна
длине волны де Бройля.
импульса движущейся частицы, если
неопределенность ее координаты равна
длине волны де Бройля.
|
Дано:
|
Решение
|
|
|
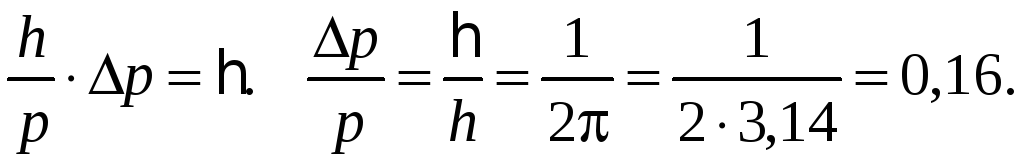
Ответ:
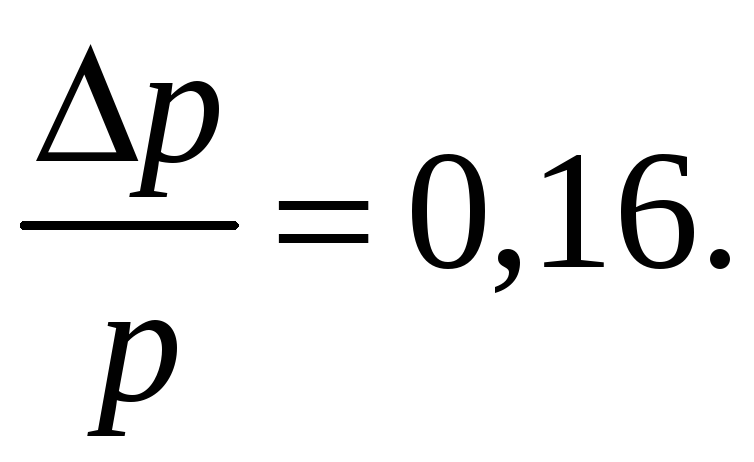
Пример 81.2. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером l = 0,2 нм.
|
Дано:
l = 0,2 нм
|
Решение
|
|
Emin– ? |
![]()
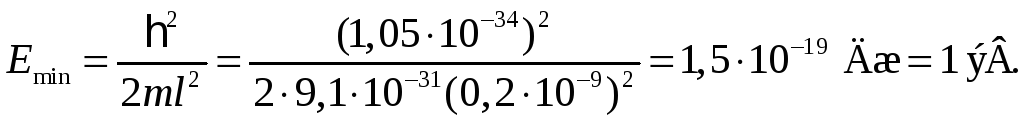
Ответ:
![]()
§ 82. Уравнение Шредингера
Волновая функция
![]()
является решением дифференциального уравнения. Получим его. Пусть микрочастица движется в потенциальном поле и ее волновая функция не зависит от времени. Можем написать
![]()
откуда
![]() не зависит от времени. Продифференцируем
ψ дважды по x.
не зависит от времени. Продифференцируем
ψ дважды по x.
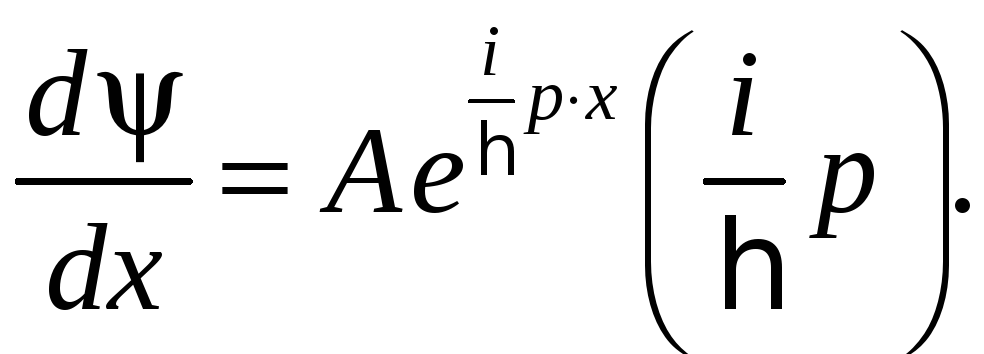
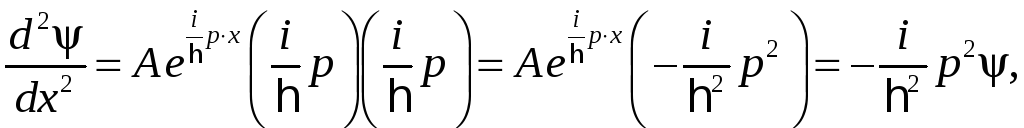
откуда
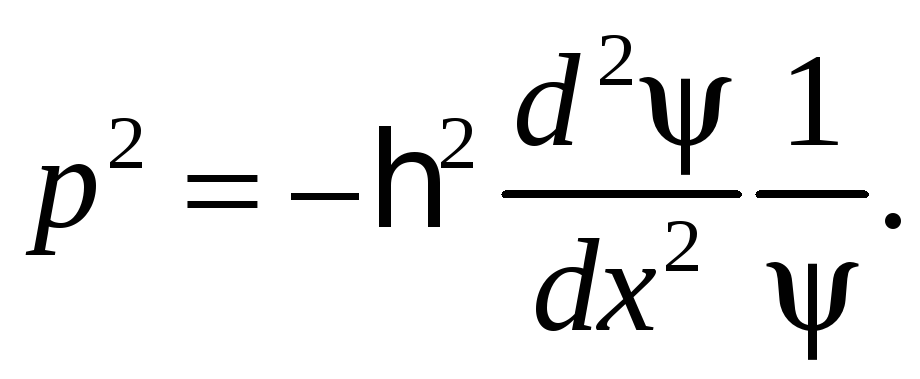
Свяжем E и p:
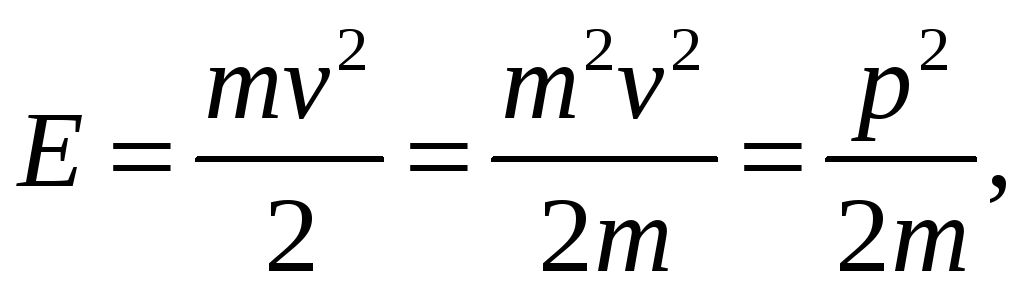
откуда
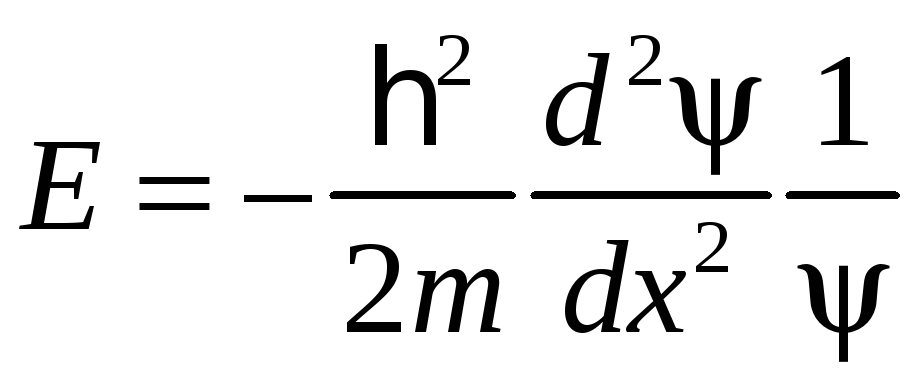
или
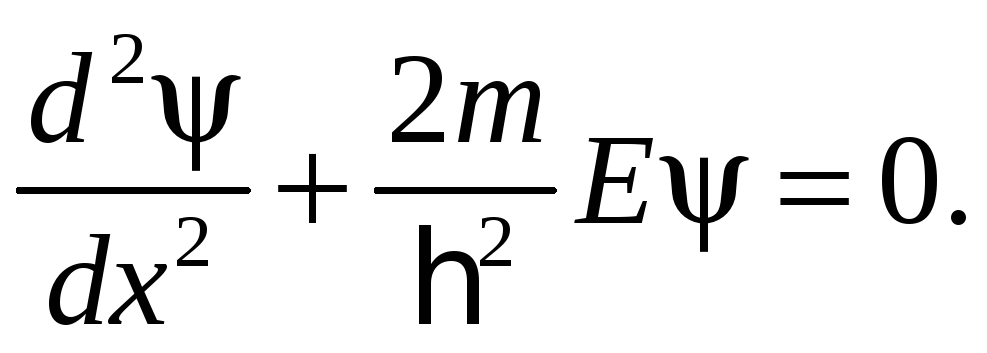 (82.1)
(82.1)
Механическая энергия микрочастицы
![]()
где
![]() — кинетическая энергия микрочастицы;
U
— потенциальная энергия микрочастицы.
В уравнении (82.1) E
=
— кинетическая энергия микрочастицы;
U
— потенциальная энергия микрочастицы.
В уравнении (82.1) E
=
![]() .
В случае потенциального поля
.
В случае потенциального поля
![]() .
Тогда имеем
.
Тогда имеем
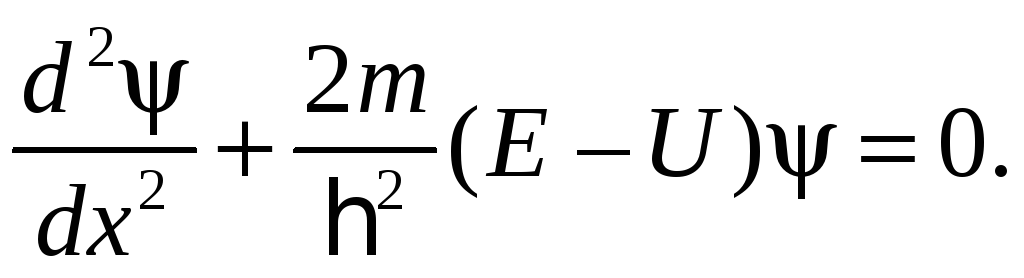 (82.2)
(82.2)
Уравнение (82.2) называют стационарным уравнением Шредингера для микрочастицы, движущейся в потенциальном поле вдоль оси x.
Уравнение Шредингера является основным уравнением квантовой механики. Оно не выводится из других уравнений, а является исходным основным предположением (постулатом), справедливость которого доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытом.