Глава 19. Квантовая механика § 79. Волны де Бройля

Рассмотрение многочисленных оптических явлений обнаруживает двоякую природу света. Такие явления, как интерференция и дифракция, свидетельствуют о том, что свет — это непрерывные электромагнитные волны. Такие явления, как фотоэффект и эффект Комптона, свидетельствуют о том, что свет — это поток дискретных частиц — фотонов.

Что же такое свет — электромагнитная волна или поток фотонов? Можно утверждать, что свет одновременно обладает свойствами электромагнитных волн и свойствами фотонов. С уменьшением длины волны (увеличением частоты) все более отчетливо проявляются корпускулярные свойства света. Наоборот, с увеличением длины волны (уменьшением частоты) основную роль играют волновые свойства света.

Французский физик Луи де Бройль в 1924 г. пришел к выводу, что корпускулярно-волновая двойственность свойств характерна не только для света. Если по мере уменьшения длины волны света все более отчетливо проявляются его корпускулярные свойства, то можно предположить существование очень коротких волн, связанных каким-то образом с частицами вещества — электронами, нейтронами, атомами, молекулами и т. д. Де Бройль обобщил соотношение (77.3) для волновых процессов, связанных с частицами, обладающими импульсом p:

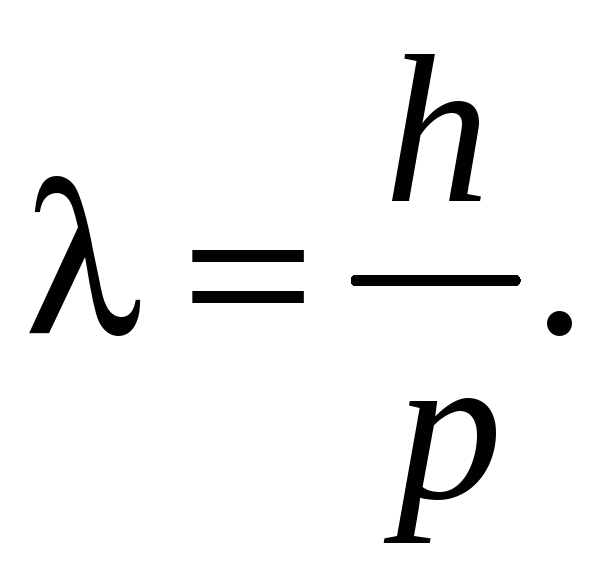(79.1)

Соотношение (79.1) называют формулой де Бройля. Для частицы массой m, движущейся со скоростью (с — скорость света),

(79.2)

Ф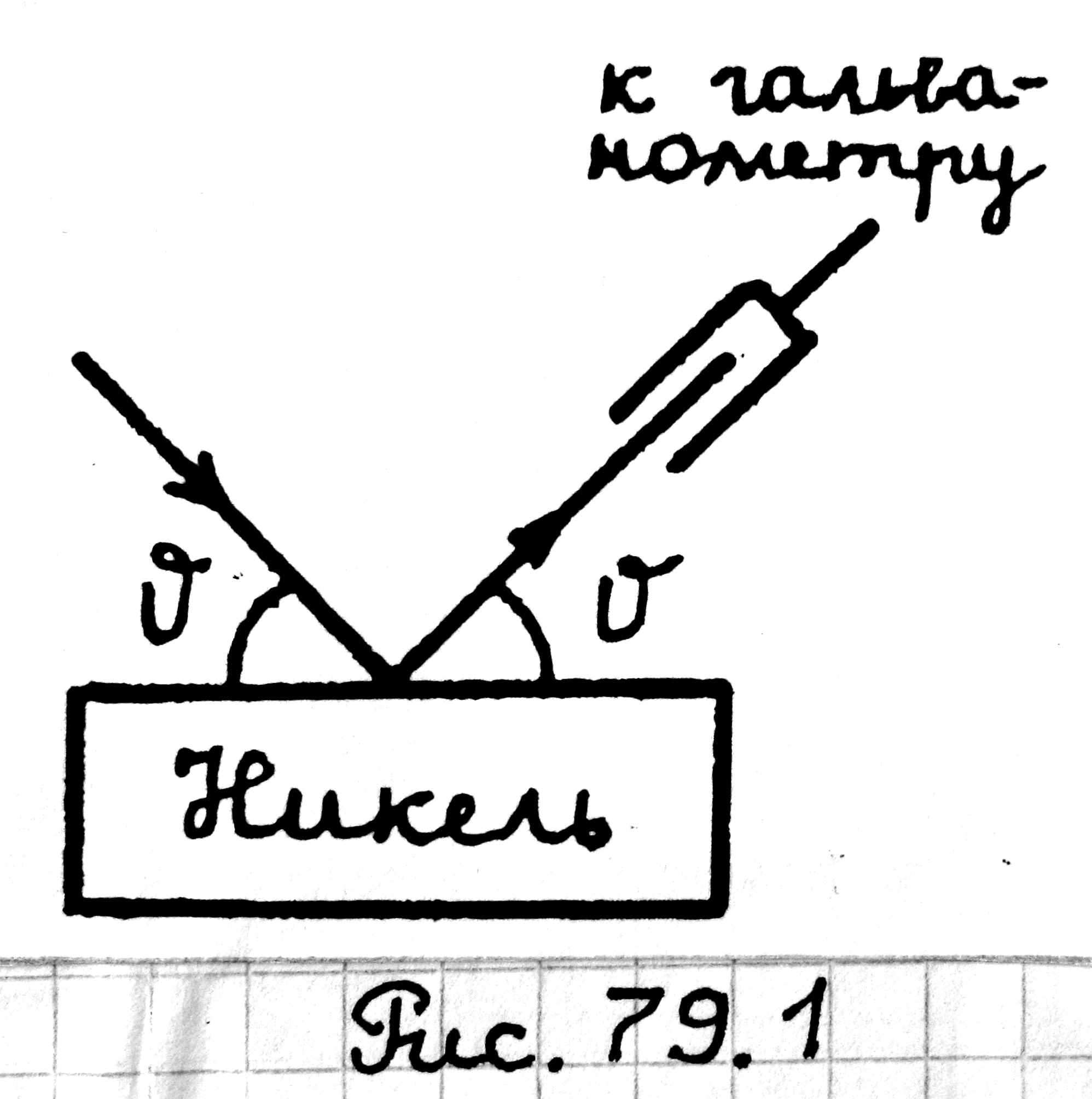 ормула де Бройля экспериментально подтвердилась, например, в опытах Дэвиссона и Джермера, наблюдавших в 1927 г. отражение пучка электронов монокристаллом никеля (рис. 79.1). Максимальная интенсивность отраженного пучка оценивалась по силе тока через гальванометр. Если пучок электронов обладает волновыми свойствами, то эти максимумы должны удовлетворять условию Брэгга – Вульфа (полученному при дифракции от кристалла рентгеновских лучей):

Рис. 79.1

(79.3)

где d — расстояние между атомными плоскостями никеля (величина известная); — угол между атомной плоскостью и направлением отраженного пучка электронов (измеряется в опыте). В опыте также измерялась скорость v электронов в пучке.

Оказалось, что длины волн λ, определенные по формулам (79.2) и (79.3) совпадают. Итак, явление наличия волновых свойств у движущихся микрочастиц было доказано.

Возникает вопрос, почему волновые свойства не обнаруживаются у макроскопических тел, например, у летящей со скоростью v = 100 м/с пули с массой m = 1 г. По формуле де Бройля (79.2) имеем

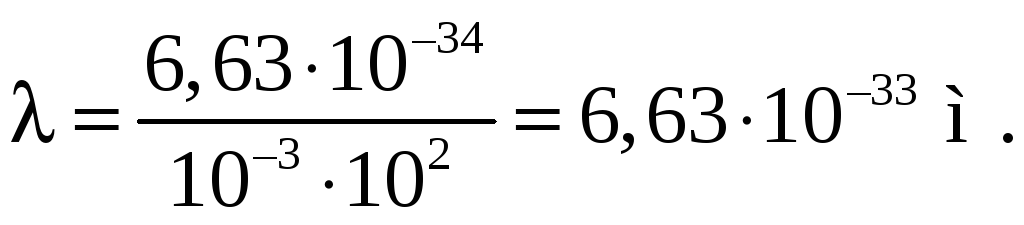
Легко сообразить, что такая длина волны никаким дифракционным опытом не может быть обнаружена. Поэтому можно считать, что волновые свойства у макроскопических тел практически отсутствуют.

Пример 79.1. Найти длину волны λ де Бройля для электрона, прошедшего ускоряющую разность потенциалов .

Дано:	Решение
λ – ?

так как v₁ = 0.

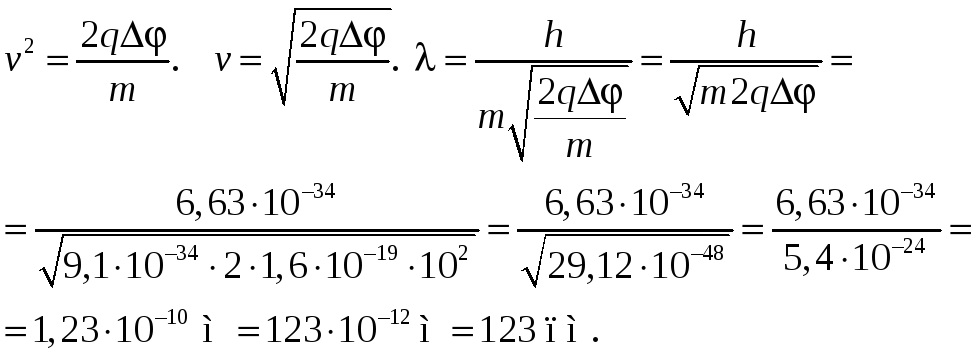
Ответ:

§ 80. Волновая функция

Какова природа волн де Бройля? Это не электромагнитные волны. Электромагнитные волны представляют собой распространяющееся в пространстве переменное электромагнитное поле. Распространение же волн де Бройля не связано с распространением в пространстве какого-либо электромагнитного поля. Можно сказать, что волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии с волнами в классической физике.

Запишем волновое уравнение плоской гармонической волны, распространяющейся вдоль оси x,

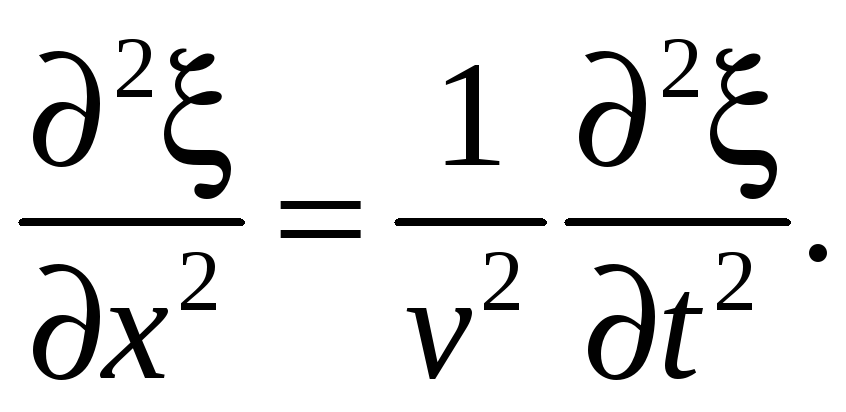(80.1)

Его решение

(80.2)

Используя формулу Эйлера

запишем выражение (80.2) в виде

или (опуская знак Re — реальная часть)

(80.3)

Рассмотрим микрочастицу, свободно движущуюся вдоль оси x. Согласно де Бройлю, ей нужно сопоставить плоскую волну

(80.4)

(в квантовой механике принято показатель экспоненты брать со знаком минус).

Запишем выражение для энергии и импульса микрочастицы

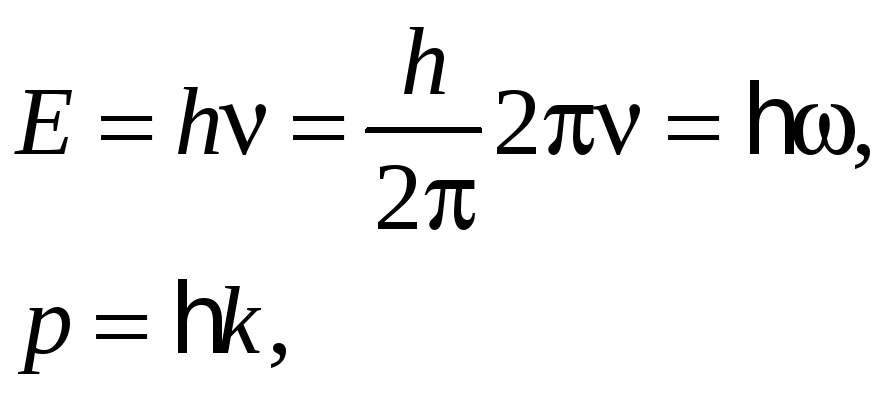
откуда

(80.5)

(80.6)

Подставляя формулы (80.5) и (80.6) в выражение (80.4), получаем

(80.7)

Функцию называют волновой функцией, или пси-функцией.

В опыте Дэвиссона и Джермера обнаруживается неодинаковое распределение пучка электронов, отраженных от кристалла, по различным направлениям, а именно, в некоторых направлениях наблюдается большее число электронов, чем в других. С волновой точки зрения, наличие максимумов числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности I волн де Бройля. Можно сказать, что интенсивность I волн де Бройля в данной точке пространства определяет плотность вероятности попадания электронов в эту точку.

Обозначим через dP вероятность нахождения микрочастицы в элементарном интервале dx оси x. Так как в вакууме интенсивность волны I = A², где A — амплитуда волны, то плотность вероятности нахождения микрочастицы в точке с координатой x (в пределах интервала dx)

(80.8)

Из выражения (80.7) следует

(80.9)

где φ и φ^* — величины комплексно сопряженные. С учетом выражения (80.9) запишем соотношение (80.8)

(80.10)

Из соотношения (80.10) следует, что квадрат модуля волновой функции имеет смысл плотности вероятности нахождения микрочастицы в точке с координатой x в пределах элементарного интервала координат dx.

Если мы знаем в каждой точке оси x, то вероятность нахождения микрочастицы в интервале координат

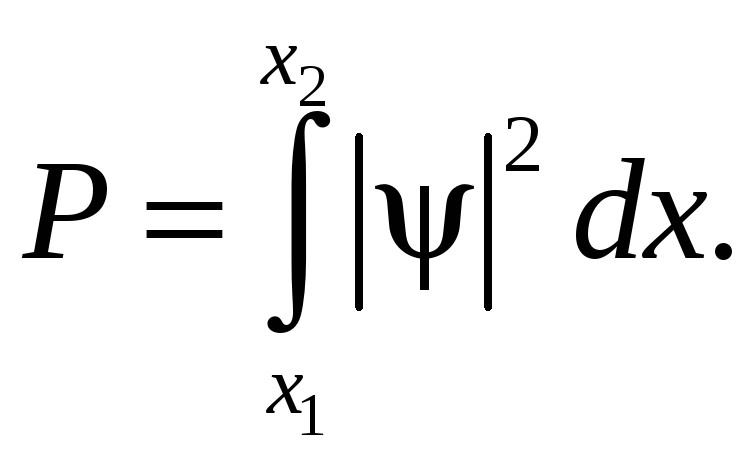(80.11)

Если микрочастица локализована только в этом интервале координат , то вероятность нахождения микрочастицы в этом интервале равна единице:

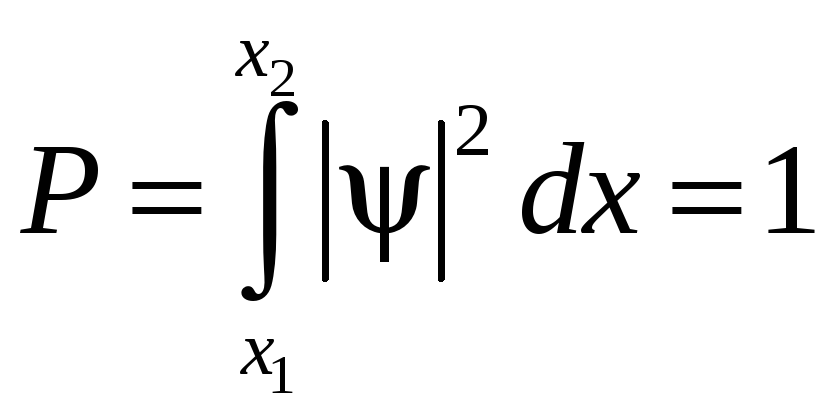(80.12)

— условие нормировки вероятности.