- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
§ 77. Фотон
Развивая гипотезу Планка (1900 г.) о том, что излучение света происходит отдельными порциями — квантами энергии, равными hν, Эйнштейн (1905 г.) предположил, что при распространении луча света, вышедшего из какого-либо источника, энергия распределяется не непрерывно во все более возрастающем пространстве. Энергия состоит из конечного числа локализованных в пространстве квантов энергии (hν). Эти световые кванты, впоследствии названные фотонами (1926 г.), движутся, не делясь на части; они могут поглощаться и испускаться как целое.
Распространение света в виде потока отдельных фотонов и квантовый характер взаимодействия света с веществом были экспериментально подтверждены (например, в опытах Боте, Иоффе и Добронравова).
До
сих пор при объяснении квантовых
оптических явлений мы использовали
только одну характеристику фотона —
его энергию
![]() .
Помимо энергии фотон обладает также
массой и импульсом.
.
Помимо энергии фотон обладает также
массой и импульсом.
Масса фотона существенно отличается от массы других микрочастиц (например, электронов). Это отличие состоит в том, что для фотона масса покоя m0 = 0. Фотон всегда (даже в веществе) движется со скоростью света c в вакууме. Этот вывод не противоречит тому, что фазовая скорость света в веществе отлична от c. Распространение света в веществе сопровождается процессами «переизлучения» — фотоны поглощаются и вновь излучаются частицами вещества.
Формула для массы фотона может быть непосредственно выведена из соотношения
![]()
выражающего взаимосвязь массы и энергии в теории относительности:
![]() (77.1)
(77.1)
Импульс фотона с учетом формулы (77.1)
![]() (77.2)
(77.2)
Если
ввести волновое число
![]() ,
то выражение (77.2) можно переписать в
виде
,
то выражение (77.2) можно переписать в
виде
![]() (77.3)
(77.3)
где
![]() Дж∙с.
Дж∙с.
Направление
импульса фотона совпадает с направлением
распространения света, характеризуемым
волновым вектором
![]() ,
модуль которого равен волновому числу.
Следовательно,
,
модуль которого равен волновому числу.
Следовательно,
![]() (77.4)
(77.4)
Таким образом, фотон, подобно любой движущейся частице, обладает энергией, массой и импульсом. Все эти корпускулярные характеристики фотона связаны с волновой характеристикой света — его частотой ν.
§ 78. Эффект Комптона
В
1923 г. американский физик Комптон
исследовал рассеяние рентгеновских
лучей (длина волны которых λ не превышает
100 нм) «легкими» веществами (графит,
парафин и т. д.). Анализируя рассеянное
излучение с помощью спектрометра, он
обнаружил, что это излучение содержит,
кроме линии первичного излучения с
длиной волны λ, другую линию с большей
длиной волны
![]() .
Оказалось, что в данных условиях опыта
(маленькая λ и небольшая атомная масса
вещества) разность
.
Оказалось, что в данных условиях опыта
(маленькая λ и небольшая атомная масса
вещества) разность
![]() не зависит от λ и природы вещества, но
увеличивается по мере возрастания угла
рассеяния
не зависит от λ и природы вещества, но
увеличивается по мере возрастания угла
рассеяния
![]() по закону
по закону
![]() (78.1)
(78.1)
(угол
рассеяния
![]() — это угол между направлениями первичного
и рассеянного излучений).
— это угол между направлениями первичного
и рассеянного излучений).
Классическая электродинамика не могла объяснить это явление, названное эффектом Комптона. Согласно ей, при рассеянии электромагнитного излучения веществом рассеянное излучение должно иметь ту же длину волны, что и первичное излучение.
В
то же время эффект Комптона легко
интерпретируется как упругое соударение
между фотоном и электроном. При этом
соударении первичный фотон с энергией
hν
передает часть своей энергии Eэ
электрону вещества, называемому
электроном отдачи. Рассеянный фотон
имеет энергию
![]() ,
а следовательно, и частоту
,
а следовательно, и частоту
![]() ,
меньшую, чем первичный фотон.
,
меньшую, чем первичный фотон.
Решая совместно уравнения, выражающие законы сохранения энергии и импульса:
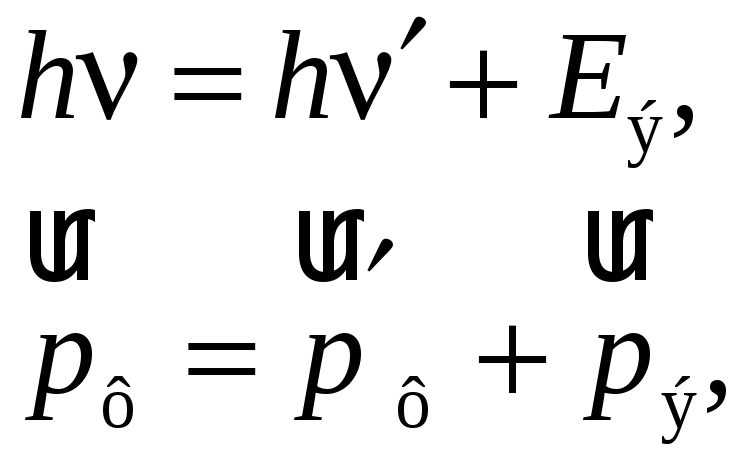
получаем соотношение (78.1), экспериментально полученное Комптоном.
Пример
78.1. Фотон с
энергией hν
= 0,75 МэВ рассеялся на свободном электроне
под углом
![]() .
Определить энергию
.
Определить энергию
![]() рассеянного фотона.
рассеянного фотона.
|
Дано:
hν = 0,75 МэВ
|
Решение
. |
|
|
![]()
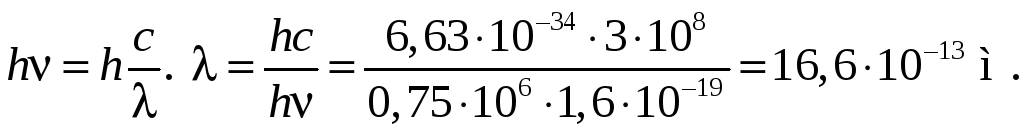

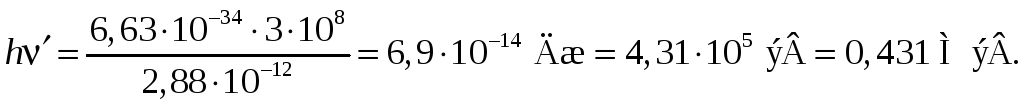
Ответ:
![]()
Пример
78.2. Рентгеновские
лучи с длиной волны λ = 20 пм испытывают
комптоновское рассеяние под углом
![]() .
Найти энергию Eэ
электрона отдачи.
.
Найти энергию Eэ
электрона отдачи.
|
Дано:
λ = 20 пм
|
Решение
|
|
Eэ – ? |
![]()
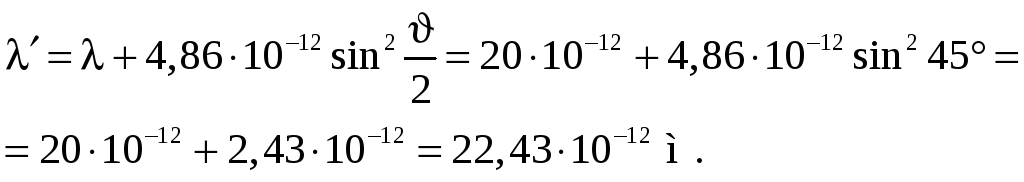
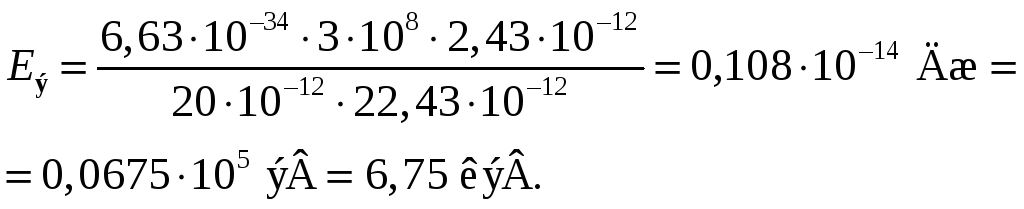
Ответ:
![]()