§ 60. Ток смещения

Максвелл выдвинул идею о симметрии во взаимодействии электрического и магнитного полей. А именно, поскольку меняющееся со временем магнитное поле порождает электрическое поле, следует ожидать, что меняющееся со временем электрическое поле порождает магнитное поле.

Продифференцируем по времени соотношение (39.5), выражающее теорему Гаусса для вектора :

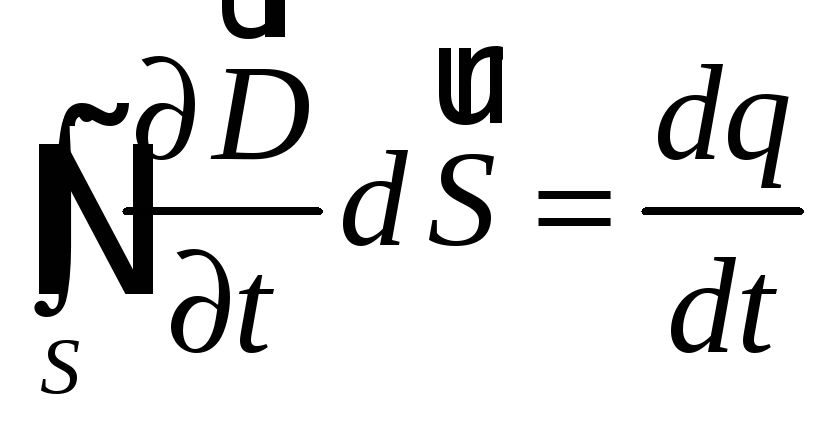(60.1)

(знак частной производной указывает на то, что вектор , являющийся функцией x, y, z, t, меняется только со временем t).

Вспомним уравнение непрерывности

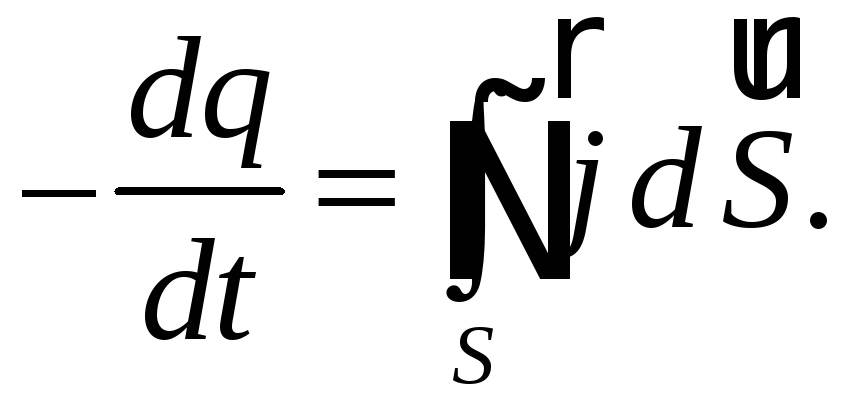(60.2)

Из соотношений (60.1) и (60.2) получаем

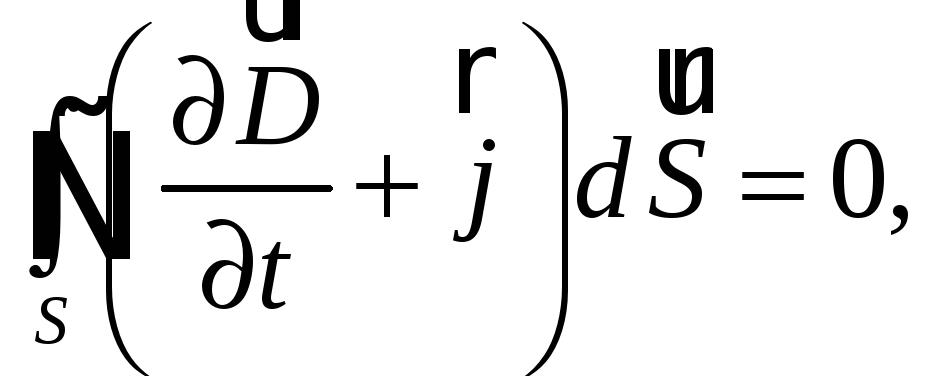(60.3)

откуда видно, что имеет размерность плотности тока. Максвелл предложил назвать

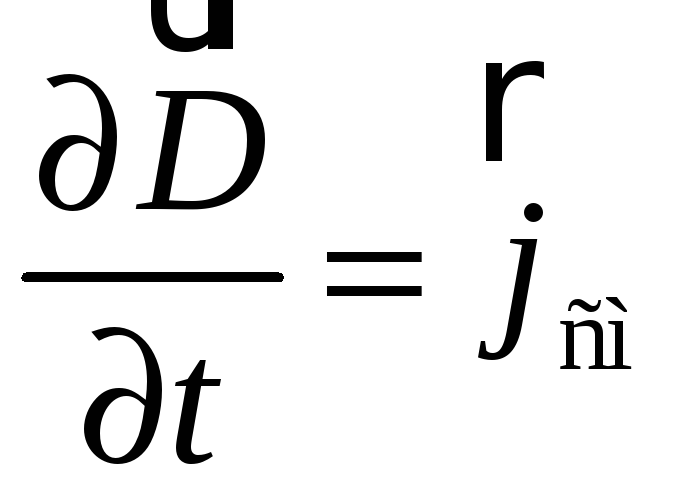(60.4)

плотностью тока смещения в данной точке пространства, равной скорости изменения вектора в этой точке.

Сила тока смещения сквозь произвольную поверхность S

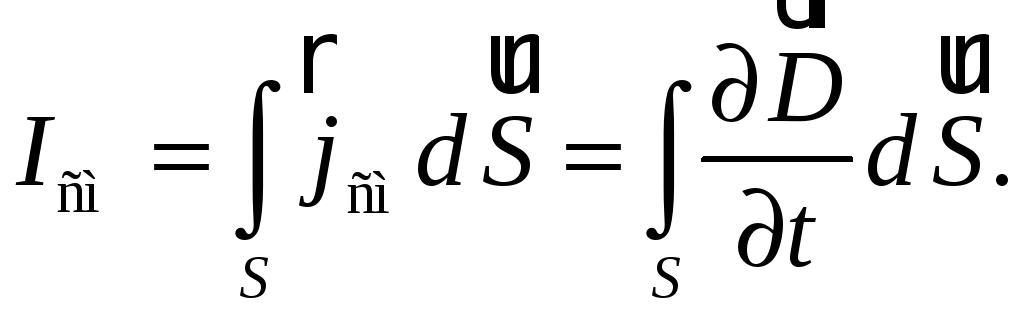(60.5)

С учетом смещения (60.5) запишем теорему о циркуляции вектора (55.5) в виде

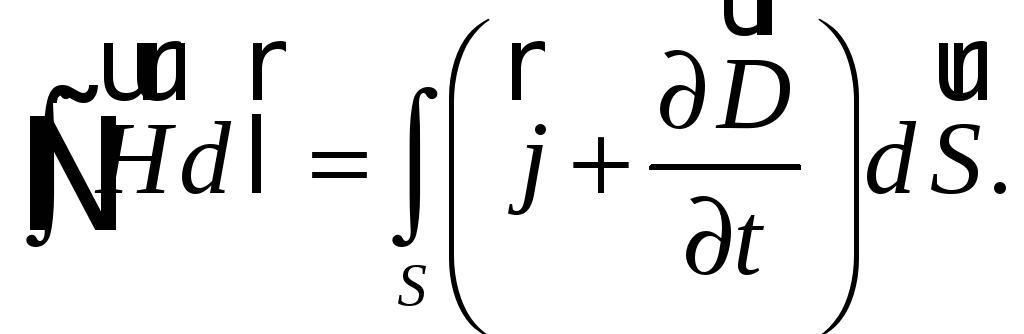(60.6)

Таким образом, магнитное поле создается не только током проводимости (обычным током, текущим по проводу), но и током смещения, причиной возникновения которого является изменение электрического поля со временем.

§ 61. Система уравнений Максвелла

Открытие тока смещения позволило Максвеллу создать единую теорию поведения электрического и магнитного полей, названную электродинамикой. Эта теория представляет собой систему уравнений, называемых уравнениями Максвелла:

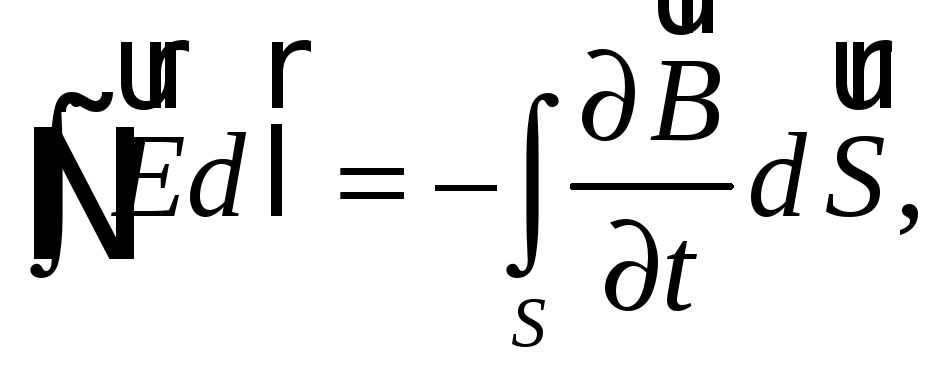(61.1)

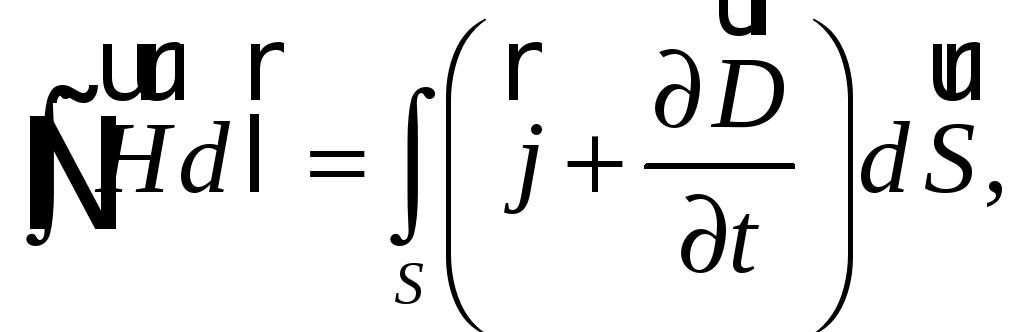(61.2)

(61.3)

(61.4)

где ρ — объемная плотность сторонних зарядов; — плотность тока проводимости.

Согласно уравнениям (61.1) и (61.3), электрическое поле возникает, когда есть электрические заряды или переменное во времени магнитное поле. Согласно уравнению (61.2), магнитное поле возникает, когда есть электрический ток или переменное во времени электрическое поле. В противном случае магнитное поле не возникает (61.4). Из уравнений Максвелла следует чрезвычайно важный вывод о том, что переменные электрические и магнитные поля неразрывно связаны друг с другом, образуя единое электромагнитное поле.

В заключение отметим, что система уравнений (61.1)–(61.4) была замкнутой, позволяющей рассчитывать электромагнитные процессы в материальной среде, ее необходимо дополнить соотношениями, связывающими , , , и :

(61.5)

(61.6)

(61.7)

Такие уравнения называют материальными.

§ 62. Электромагнитные волны

Систему уравнений Максвелла, записанную для однородной непроводящей среды, где и , можно свести к двум дифференциальным уравнениям второго порядка с постоянными коэффициентами

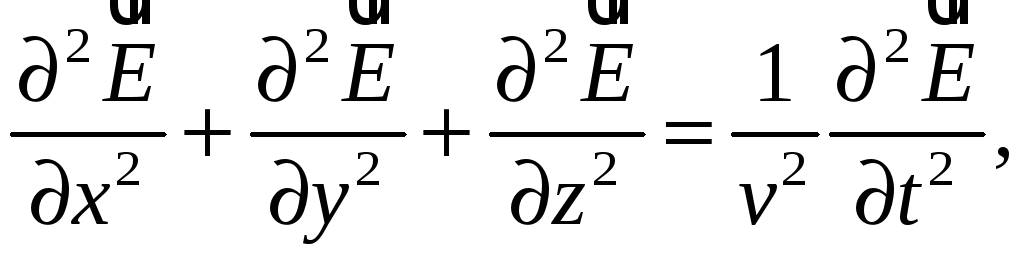(62.1)

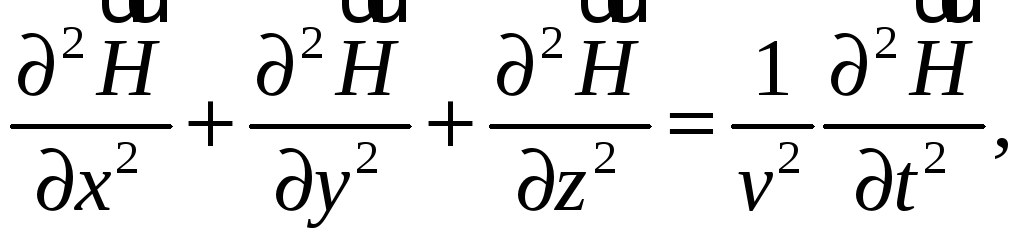(62.2)

которые являются волновыми уравнениями двух плоских гармонических волн, представляющих собой синхронное (с одинаковой фазой) однонаправленное распространение в среде колебаний векторов и :

(62.3)

(62.4)

(формулы (62.3) и (62.4) записаны для частного случая распространения колебаний вдоль оси x).

Следовательно, электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов — и распространяться в среде в виде электромагнитных волн со скоростью

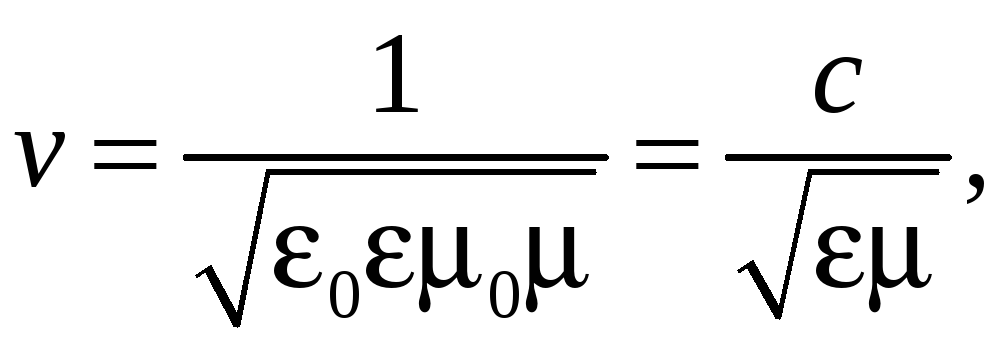(62.5)

где 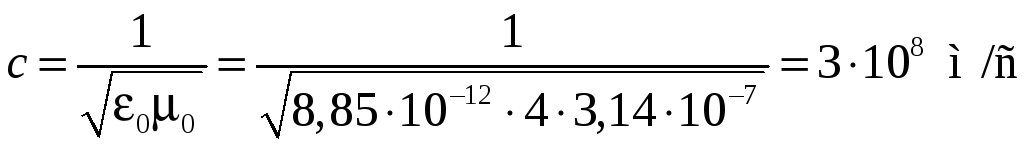— скорость электромагнитных волн в вакууме.

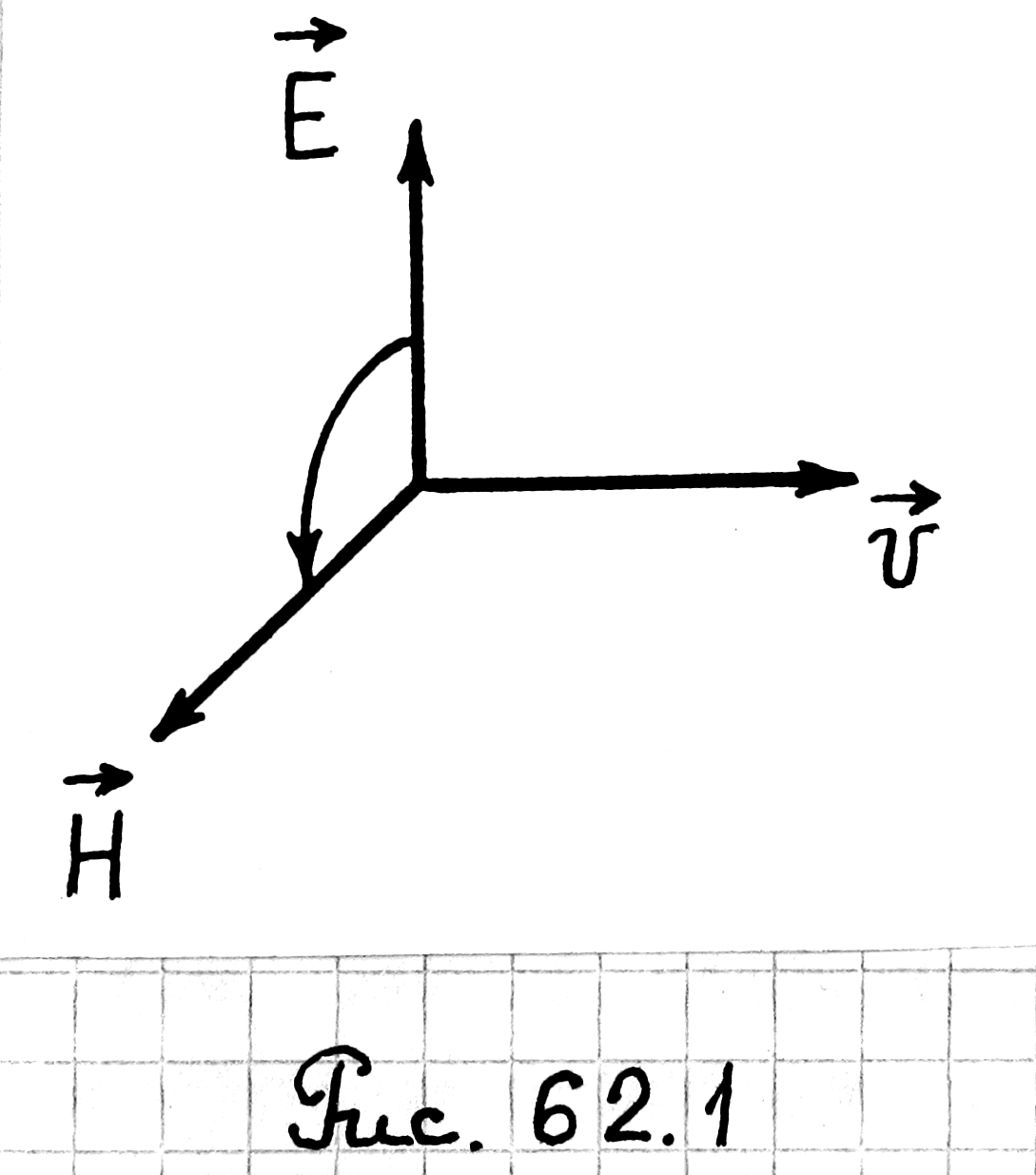
Рис.62.1

Векторы и взаимно перпендикулярны и образуют с направлением распространения волны (вектором скорости волны) правовинтовую систему (рис. 62.1). Из синхронности колебаний векторов и и вытекает соотношение (62.6)

где E и H — модули векторов и .

Электромагнитные волны переносят энергию. Объемная плотность энергии электромагнитного поля (см. формулы (42.5) и (58.5))

(62.7)

С учетом соотношения (62.6) перепишем выражение (62.7) в виде

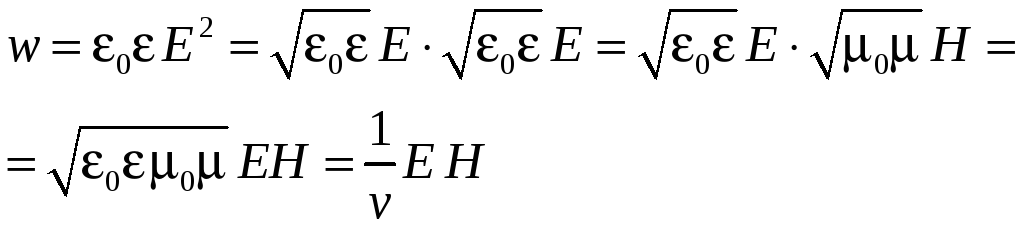(62.8)

(мы учли формулу (62.5)).

Умножим объемную плотность w энергии электромагнитного поля на скорость v электромагнитной волны и обозначим это произведение буквой S:

(62.9)

Произведение wv имеет размерность — размерность плотности потока электромагнитной энергии, по определению равной электромагнитной энергии, переносимой электромагнитной волной за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны.

Назовем вектор вектором Пойнтинга, модуль которого равен плотности потока электромагнитной энергии, а направление совпадает с направлением распространения электромагнитной волны.

Так как векторное произведение векторов и

также совпадает с направлением распространения электромагнитной волны (см. рис. 62.1), то с учетом выражения (62.8) можем написать

(62.10)