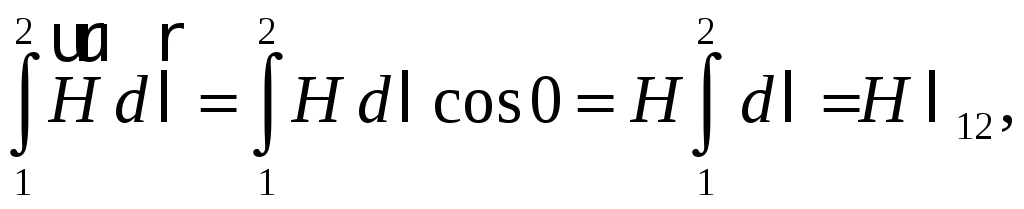- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
§ 54. Намагничивание магнетика
В
настоящее время установлено, что молекулы
многих веществ обладают собственным
магнитным моментом
![]() ,
обусловленным внутренним круговым
движением зарядов (молекулярным
током).
,
обусловленным внутренним круговым
движением зарядов (молекулярным
током).
Такую молекулу можно представить в виде элементарного контура с током. Магнитные моменты молекул ориентированы хаотически из-за теплового движения молекул. Есть вещества, молекулы которых не обладают собственным магнитным моментом.
Под
действием внешнего магнитного поля с
магнитной индукцией
![]() те и другие вещества намагничиваются,
и поэтому в этом случае их называют
магнетиками. Собственные магнитные
моменты молекул магнетика устанавливаются
по полю (
те и другие вещества намагничиваются,
и поэтому в этом случае их называют
магнетиками. Собственные магнитные
моменты молекул магнетика устанавливаются
по полю (![]() ).
).
В
молекулах, не обладающих собственным
магнитным моментом, индуцируются
элементарные круговые токи,
![]() которых тоже устанавливаются по полю.
которых тоже устанавливаются по полю.
Для количественного описания намагничивания магнетика берут магнитный момент единицы объема магнетика
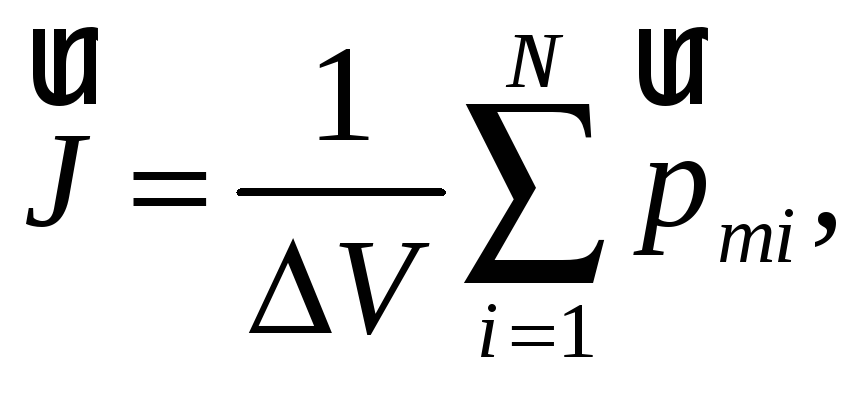 (54.1)
(54.1)
где
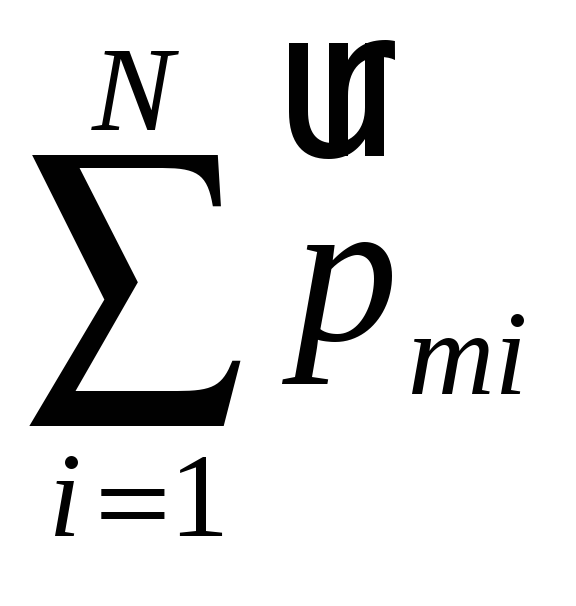 — сумма магнитных моментов N
молекул, заключенных в элементарном
(очень малом) объеме
— сумма магнитных моментов N
молекул, заключенных в элементарном
(очень малом) объеме
![]() магнетика. Вектор
магнетика. Вектор
![]() называют намагниченностью
магнетика.
называют намагниченностью
магнетика.
На
рис. 54.1
изображен схематически намагниченный
однородный магнетик. Из рисунка видно,
что намагничивание сопровождается
возникновением тока
![]() ,
текущего по боковой поверхности магнетика
(молекулярные токи в местах соприкосновения
компенсируются, так как текут в
противоположных направлениях).
,
текущего по боковой поверхности магнетика
(молекулярные токи в местах соприкосновения
компенсируются, так как текут в
противоположных направлениях).
Этот ток называют током намагничивания, в отличие от обычного тока, текущего по проводнику и поэтому называемого током проводимости.
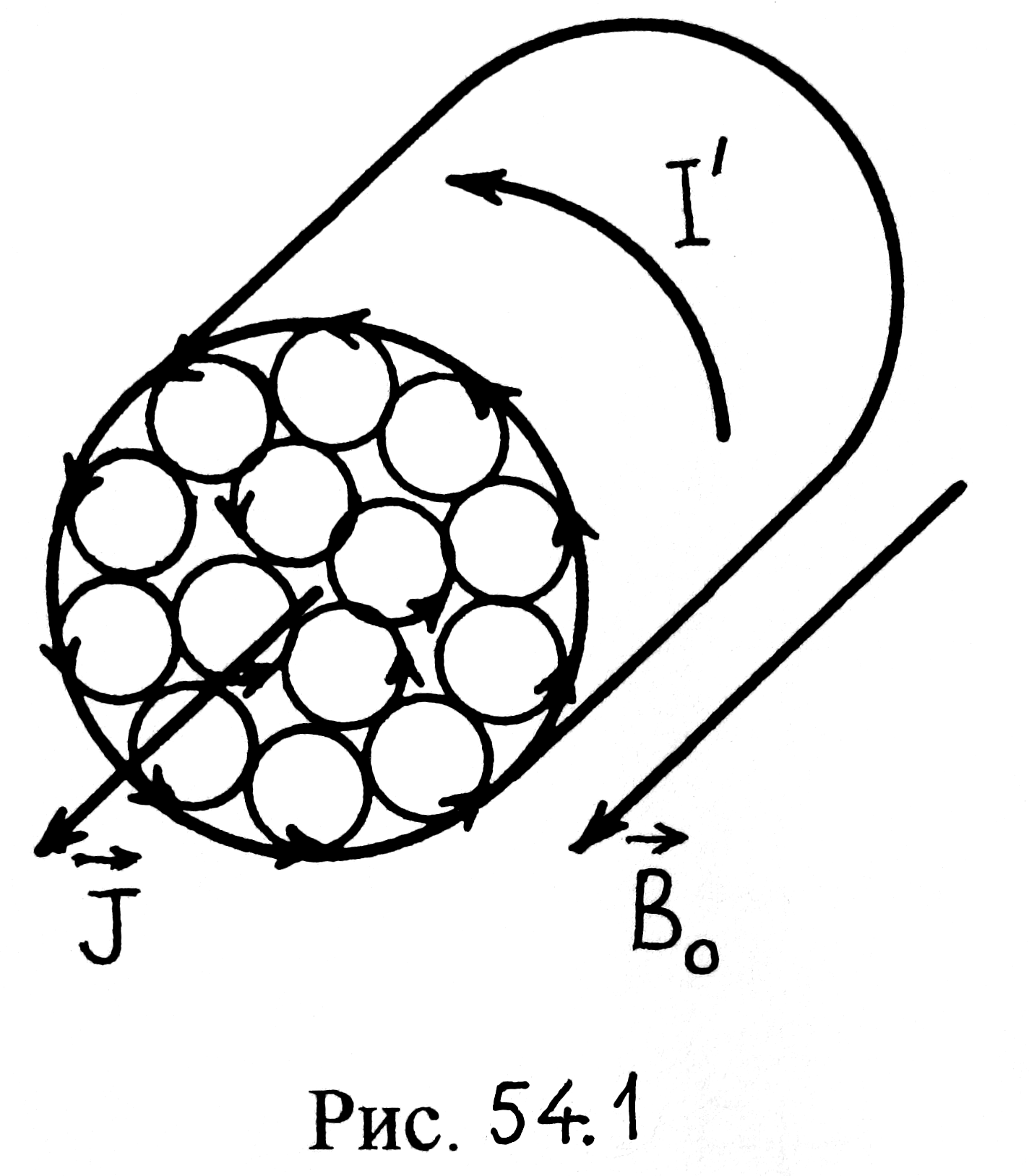
Рис. 54.1
В
результате появления тока намагничивания
в магнетике возникает магнитное поле,
создаваемое этим током. Магнитная
индукция
![]() поля в магнетике равна сумме магнитных
индукций
поля в магнетике равна сумме магнитных
индукций
![]() поля, создаваемого током проводимости
(внешнего поля), и
поля, создаваемого током проводимости
(внешнего поля), и
![]() поля, создаваемого током намагничивания:
поля, создаваемого током намагничивания:
![]() (54.2)
(54.2)
§ 55. Вектор
Теорема
о циркуляции вектора
![]() в магнетике имеет вид
в магнетике имеет вид
![]() (55.1)
(55.1)
где
I
и
![]() — токи проводимости и намагничивания,
охватываемые контуром. Расчет вектора
— токи проводимости и намагничивания,
охватываемые контуром. Расчет вектора
![]() в магнетике с использованием соотношения
(55.1) затруднителен, так как заранее не
известен ток намагничивания в магнитном
поле. Это затруднение можно обойти,
воспользовавшись теоремой о циркуляции
вектора
в магнетике с использованием соотношения
(55.1) затруднителен, так как заранее не
известен ток намагничивания в магнитном
поле. Это затруднение можно обойти,
воспользовавшись теоремой о циркуляции
вектора
![]() :
:
![]() (55.2)
(55.2)
циркуляция
вектора
![]() по произвольному контуру равна
по произвольному контуру равна
![]() ,
где
,
где
![]() — алгебраическая сумма токов
намагничивания, охватываемых этим
контуром. Ток считается положительным,
если его направление связано с направлением
обхода по контуру правилом правого
винта (если вращать винт в направлении
обхода по контуру, то направление
движения винта должно показывать
направление тока). В противном случае
ток считается отрицательным.
— алгебраическая сумма токов
намагничивания, охватываемых этим
контуром. Ток считается положительным,
если его направление связано с направлением
обхода по контуру правилом правого
винта (если вращать винт в направлении
обхода по контуру, то направление
движения винта должно показывать
направление тока). В противном случае
ток считается отрицательным.
Подставляя
![]()
в соотношение (55.1), получаем
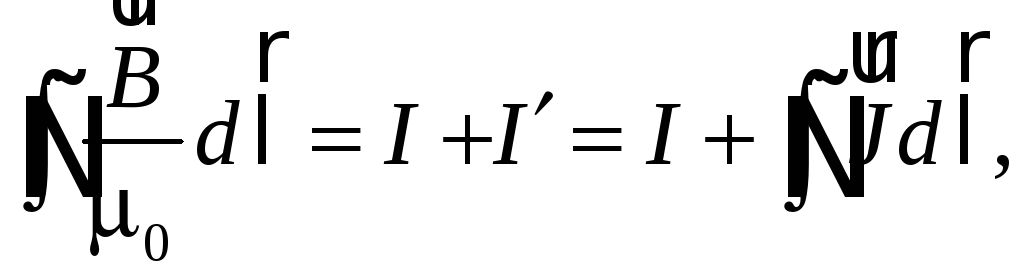
откуда
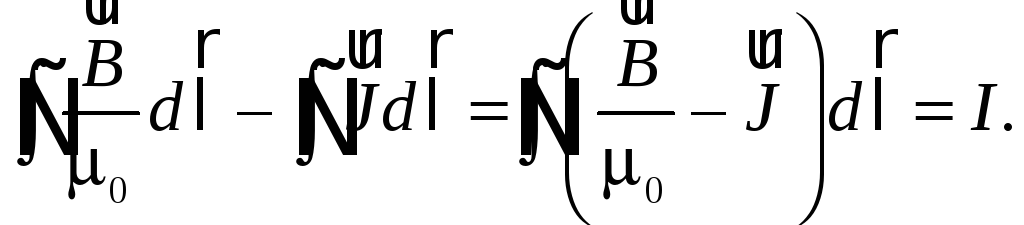 (55.3)
(55.3)
Введем вектор
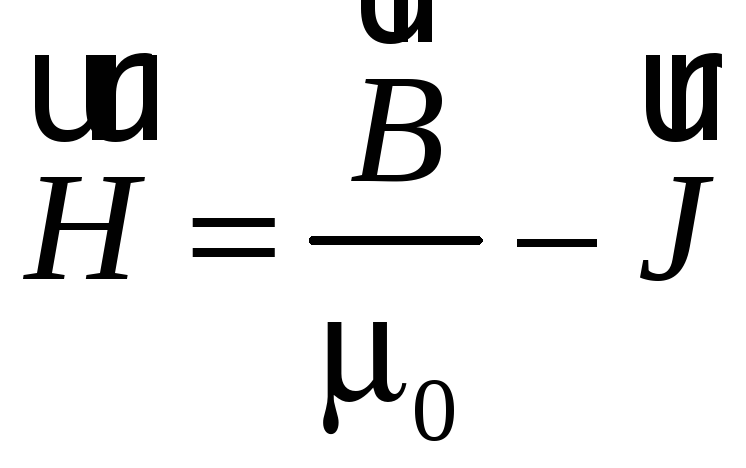 (55.4)
(55.4)
и
запишем выражение потока вектора
![]() в виде
в виде
![]() (55.5)
(55.5)
которое
представляет теорему
о циркуляции вектора
![]() :
циркуляция вектора
:
циркуляция вектора
![]() по произвольному контуру равна I,
где I
— алгебраическая сумма токов проводимости,
охватываемых этим контуром. Правило
знаков для токов то же, что и в случае
циркуляции вектора
по произвольному контуру равна I,
где I
— алгебраическая сумма токов проводимости,
охватываемых этим контуром. Правило
знаков для токов то же, что и в случае
циркуляции вектора
![]() (см. § 50).
(см. § 50).
Для многих магнетиков
![]() (55.6)
(55.6)
где
χ — безразмерная величина, называемая
магнитной
восприимчивостью
вещества. Эта величина не зависит от
![]() и является характеристикой магнетика.
Она может быть как положительной, так
и отрицательной. Магнетики с
и является характеристикой магнетика.
Она может быть как положительной, так
и отрицательной. Магнетики с
![]() называют парамагнетиками,
с
называют парамагнетиками,
с
![]() — диамагнетиками.
У парамагнетиков векторы
— диамагнетиками.
У парамагнетиков векторы
![]() и
и
![]() имеют одинаковое направление, у
диамагнетиков — противоположное.
имеют одинаковое направление, у
диамагнетиков — противоположное.
Подставляя выражение (55.6) в соотношение (55.4), получаем
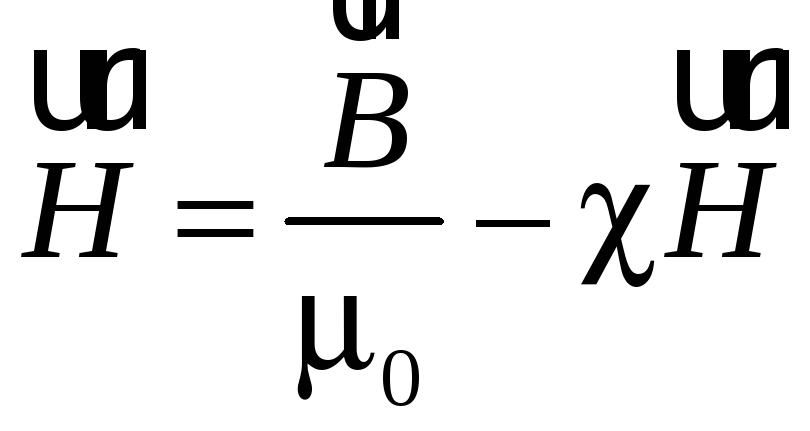
или
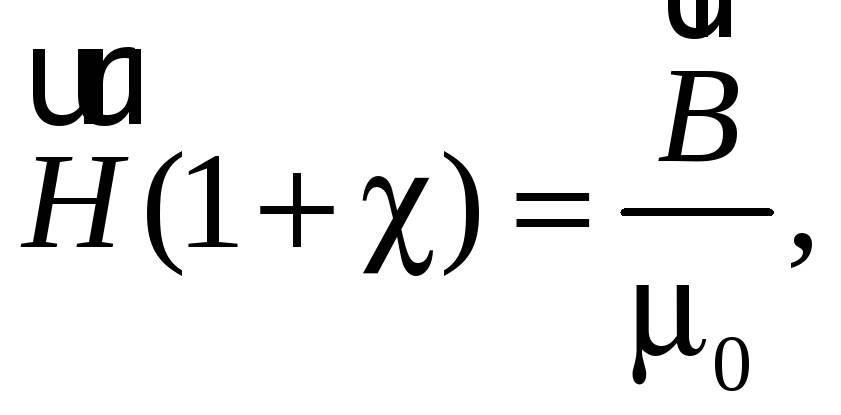
откуда
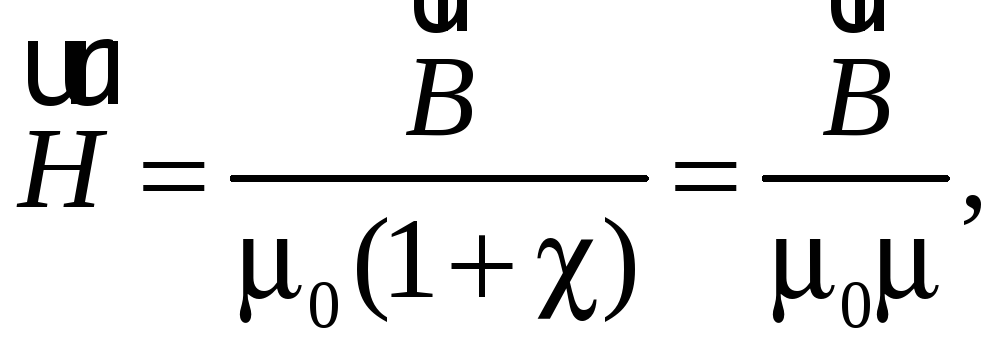 (55.7)
(55.7)
где
![]() — безразмерная положительная величина,
называемая магнитной
проницаемостью
вещества. Эта величина, как и χ, является
характеристикой магнетика. Для вакуума
— безразмерная положительная величина,
называемая магнитной
проницаемостью
вещества. Эта величина, как и χ, является
характеристикой магнетика. Для вакуума
![]() .
У парамагнетиков
.
У парамагнетиков
![]() ,
у диамагнетиков
,
у диамагнетиков
![]() .
Так как у пара- и диамагнетиков χ очень
мало (порядка 10–6–10–3),
их магнитные проницаемости мало
отличаются от единицы.
.
Так как у пара- и диамагнетиков χ очень
мало (порядка 10–6–10–3),
их магнитные проницаемости мало
отличаются от единицы.
Из соотношения (55.7) имеем
![]() (55.8)
(55.8)
Следовательно,
используя теорему о циркуляции вектора
![]() ,
можно определить вектор
,
можно определить вектор
![]() в любой точке магнитного поля в магнетике,
а затем из соотношения (55.8) найти магнитную
индукцию
в любой точке магнитного поля в магнетике,
а затем из соотношения (55.8) найти магнитную
индукцию
![]() поля в этой точке.
поля в этой точке.
Пример 55.1. Соленоид, по которому течет ток силой I, заполнен магнетиком с магнитной проницаемостью μ. Число витков на единице длины соленоида равно n. Найти магнитную индукцию B поля в соленоиде.
|
Дано:
I
μ
n |
Решение
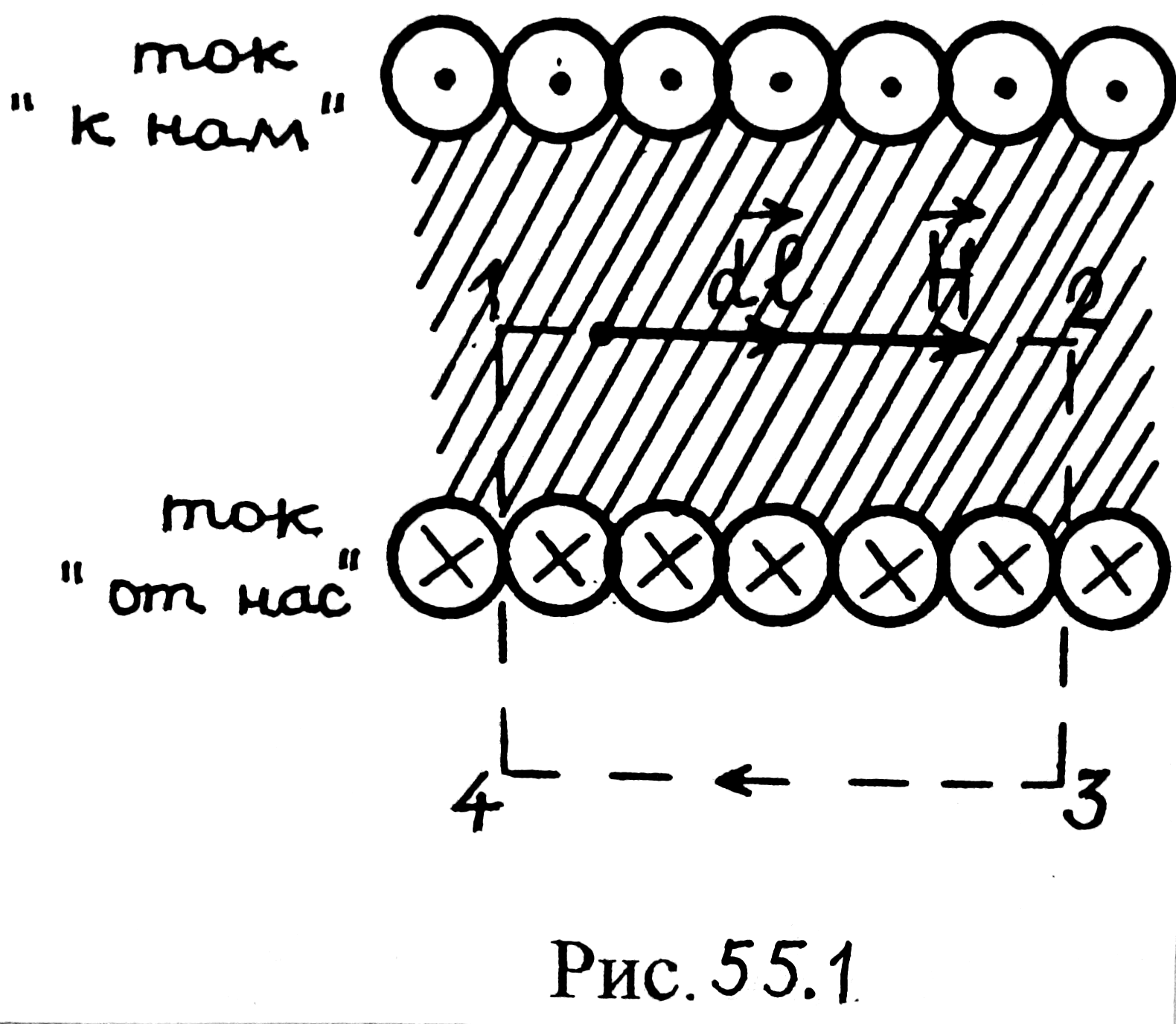
Изобразим продольный разрез соленоида (рис. 55.1).
Возьмем
произвольную точку внутри соленоида
и проведем через эту точку контур
прямоугольника, как показано на рис.
55.1. Определим циркуляцию вектора
Можем написать |
|
В – ? |
|
|
Рис. 55.1 |
В соотношении (55.9)
|
где
ℓ12
— длина стороны 12 прямоугольника (мы
учли, что H
= const,
так как сторона 12 является одной из
линий вектора
![]() ),
),
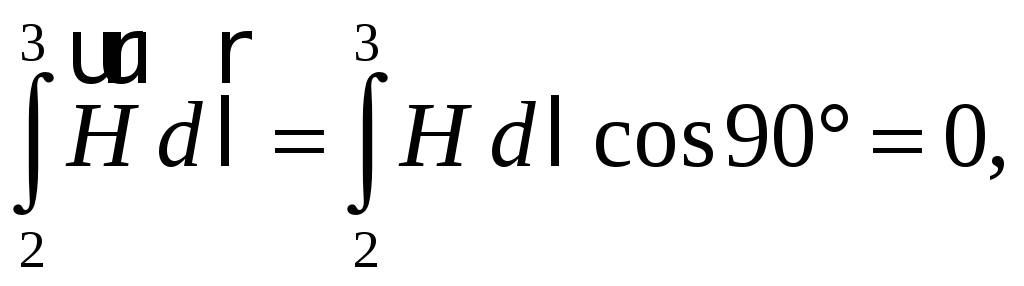
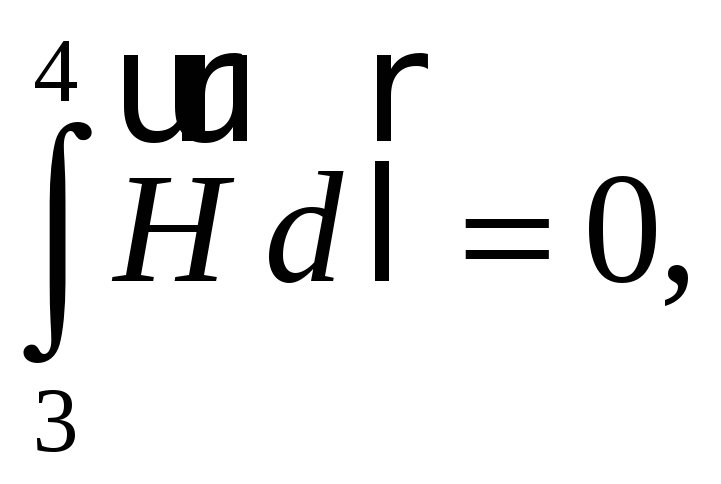
так
как вне соленоида
![]() ,
,
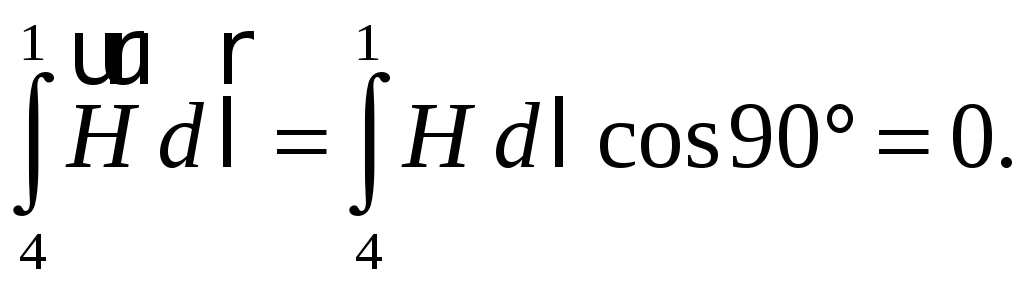
Таким образом,
![]() (55.10)
(55.10)
Согласно
теореме о циркуляции вектора
![]() (55.5)
(55.5)
![]() (55.11)
(55.11)
где N — число витков на длине ℓ12 соленоида, откуда
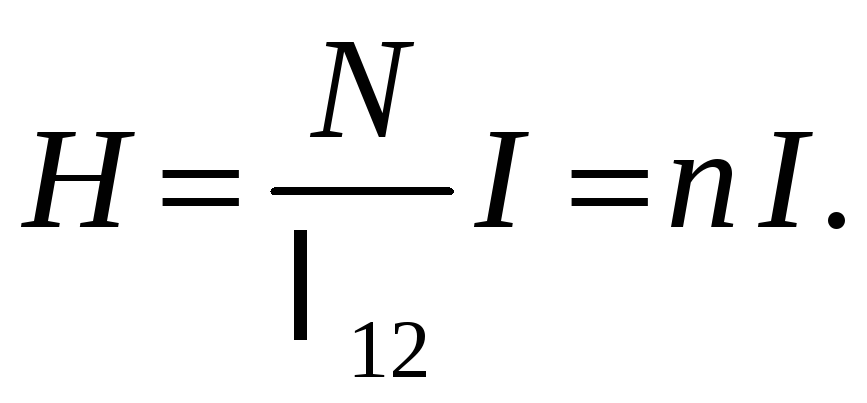 (55.12)
(55.12)
Воспользовавшись соотношением (5.8), находим магнитную индукцию B:
![]() (55.13)
(55.13)

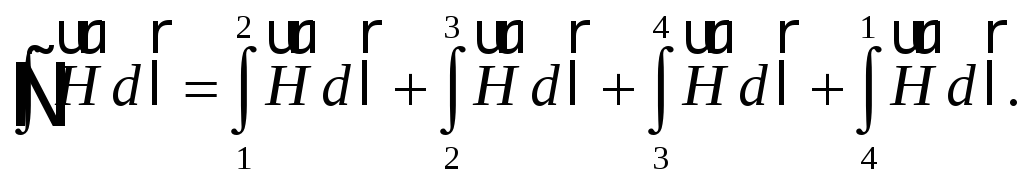 (55.9)
(55.9)