§ 48. Закон Био – Савара
Электрический ток, представляющий собой упорядоченное движение точечных зарядов, создает магнитное поле. Рассмотрим стационарное магнитное поле постоянного электрического тока, протекающего по металлическому проводу с площадью поперечного сечения S. Получим выражение, позволяющее определить магнитную индукцию в любой точке этого поля.
Каждый
элемент dℓ
длины провода с током представляет
собой постоянную совокупность точечных
зарядов (электронов) с зарядом dq,
движущихся со средней скоростью
упорядоченного движения. Элемент dℓ
создает на расстоянии r
от него магнитную индукцию
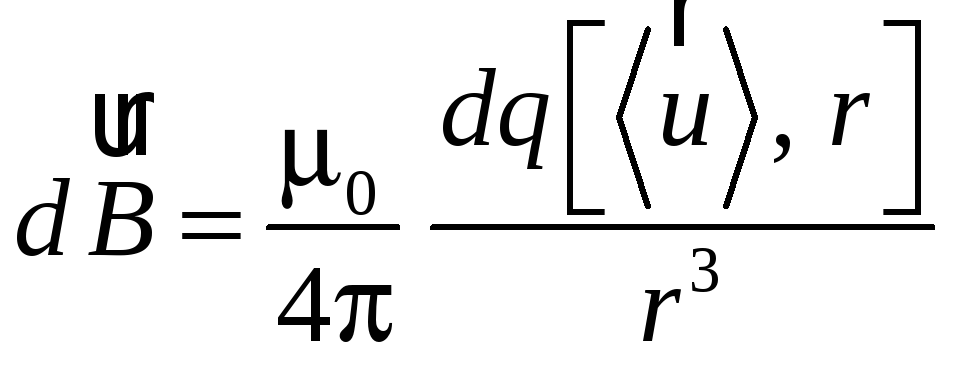(48.1)
(см. формулу (48.6)). Можем написать
(48.2)
где ρ — объемная плотность носителей тока (электронов); dV — объем элемента dℓ провода,
(48.3)
(см. формулу (43.3)). С учетом выражений (48.2) и (48.3) соотношение (48.1) примет вид
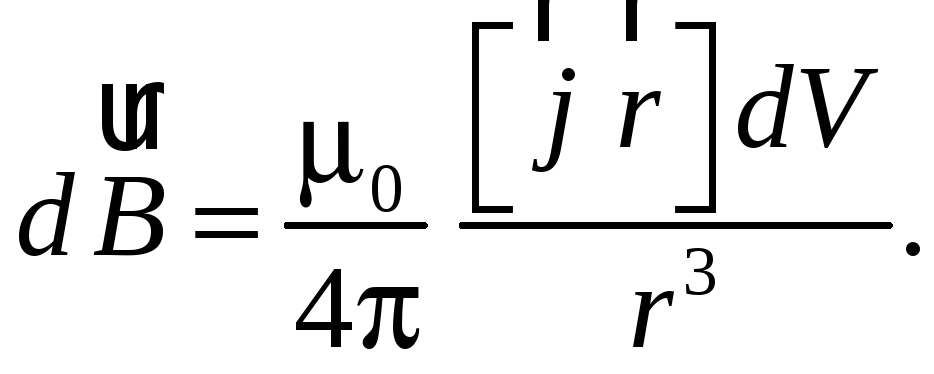(48.4)
Можем написать
(48.5)
(см.
формулу (43.6)). Введем вектор
,
модуль которого равен dℓ,
а направление совпадает с направлением
тока (вектора
).
Тогда выражение (48.5) запишем в виде
(48.6)
Подставляя формулу (48.6) в соотношение (48.4), получаем
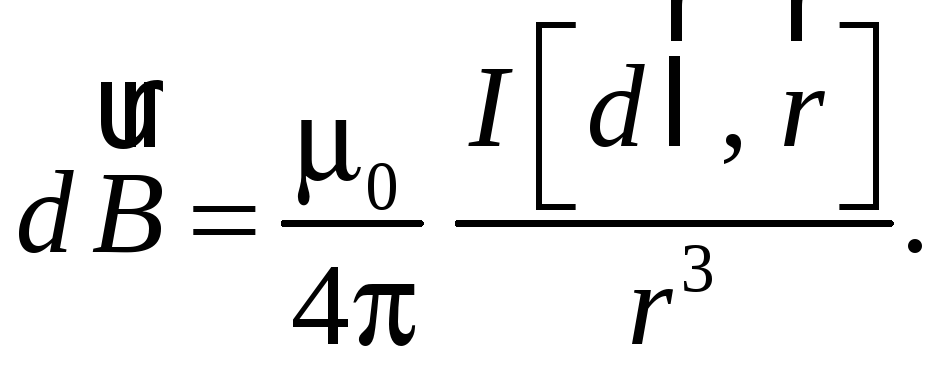(48.7)
Соотношение
(48.7) называют законом Био – Савара.
Закон Био – Савара определяет
магнитную индукцию поля, создаваемого
элементом dℓ
провода с током на расстоянии r
от него. Направления векторов
,
и
связаны правилом правого винта (если
направить указательный палец правой
руки по вектору
,
а средний — по вектору
,
то отогнутый большой палец покажет
направление вектора
(рис. 48.1)).
Магнитная индукция
перпендикулярна плоскости, в которой
лежат векторы
и
.
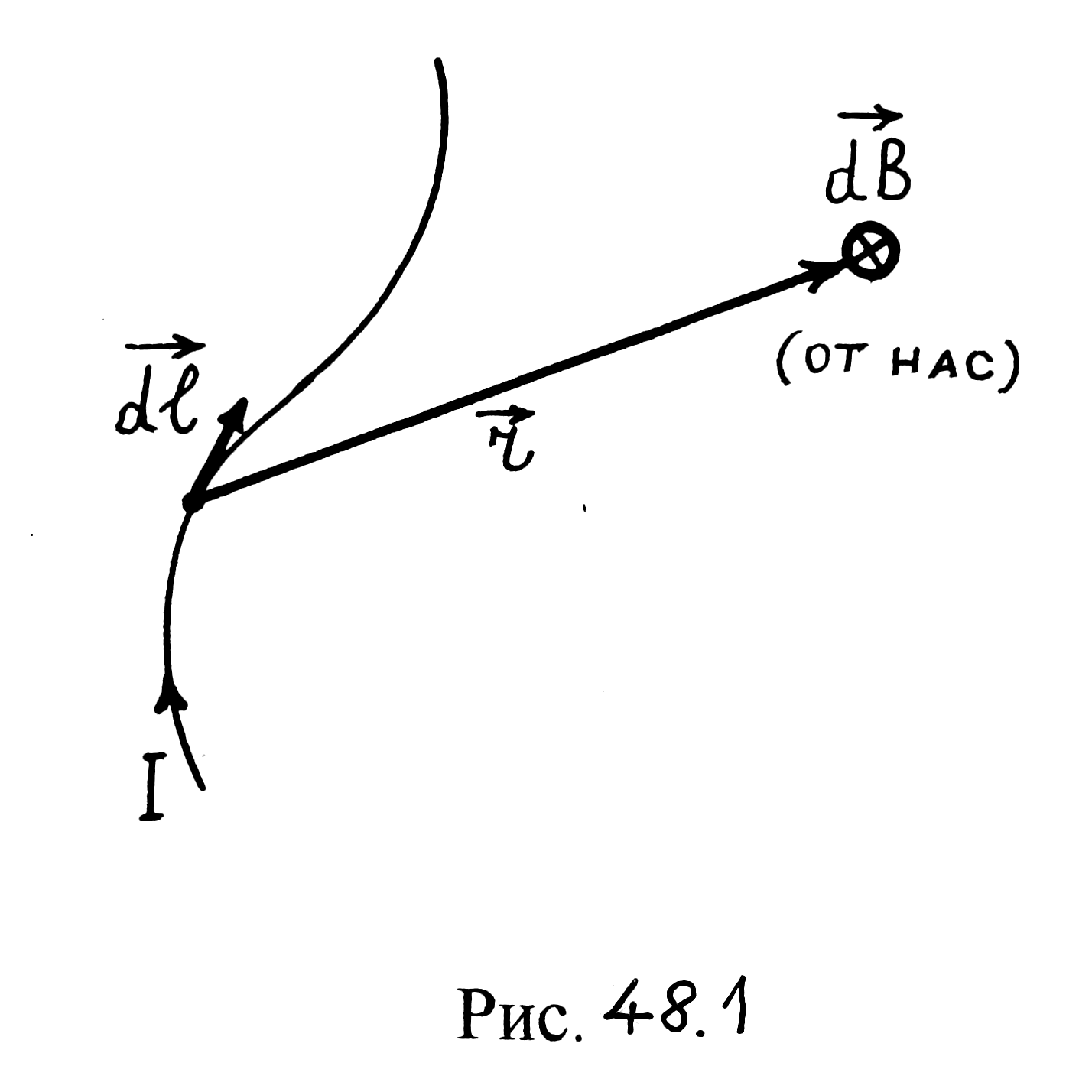
Рис. 48.1
Чтобы
получить магнитную индукцию
поля, создаваемого всем проводом с током
в интересующей нас точке, надо
проинтегрировать соотношение (48.7) по
длине провода.
Линии
вектора
магнитного поля, создаваемого постоянным
электрическим полем, текущим по
прямолинейному проводу, представляют
собой концентрические окружности с
центрами, лежащими на оси провода.
Направление линий определяют по правилу
правого винта (если ввинчивать винт по
направлению тока, то направление вращения
винта покажет направление линий вектора
)
(см. рис. 48.2,
где представлено поперечное сечение
провода с током).
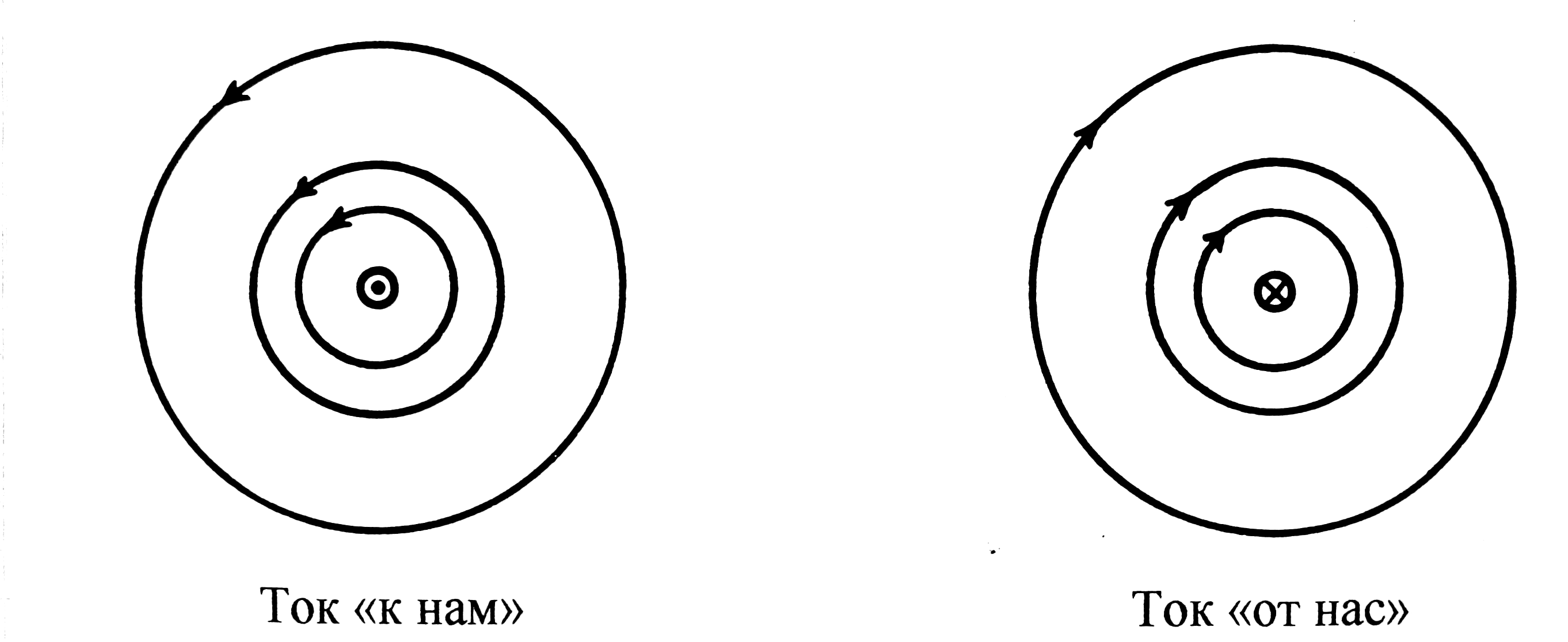
Рис. 48.2
Направление
вектора
в точках на оси кругового провода, по
которому течет постоянный электрический
ток, определяют по правилу правого винта
(если вращать винт в направлении тока,
то направление движения винта покажет
направление вектора
)
(см. рис. 48.3,
где ось кругового провода перпендикулярна
плоскости рисунка).
Рис. 48.3
§ 49. Теорема Гаусса для поля вектора
Возьмем
элементарную площадку dS
в поле вектора
(рис. 49.1).
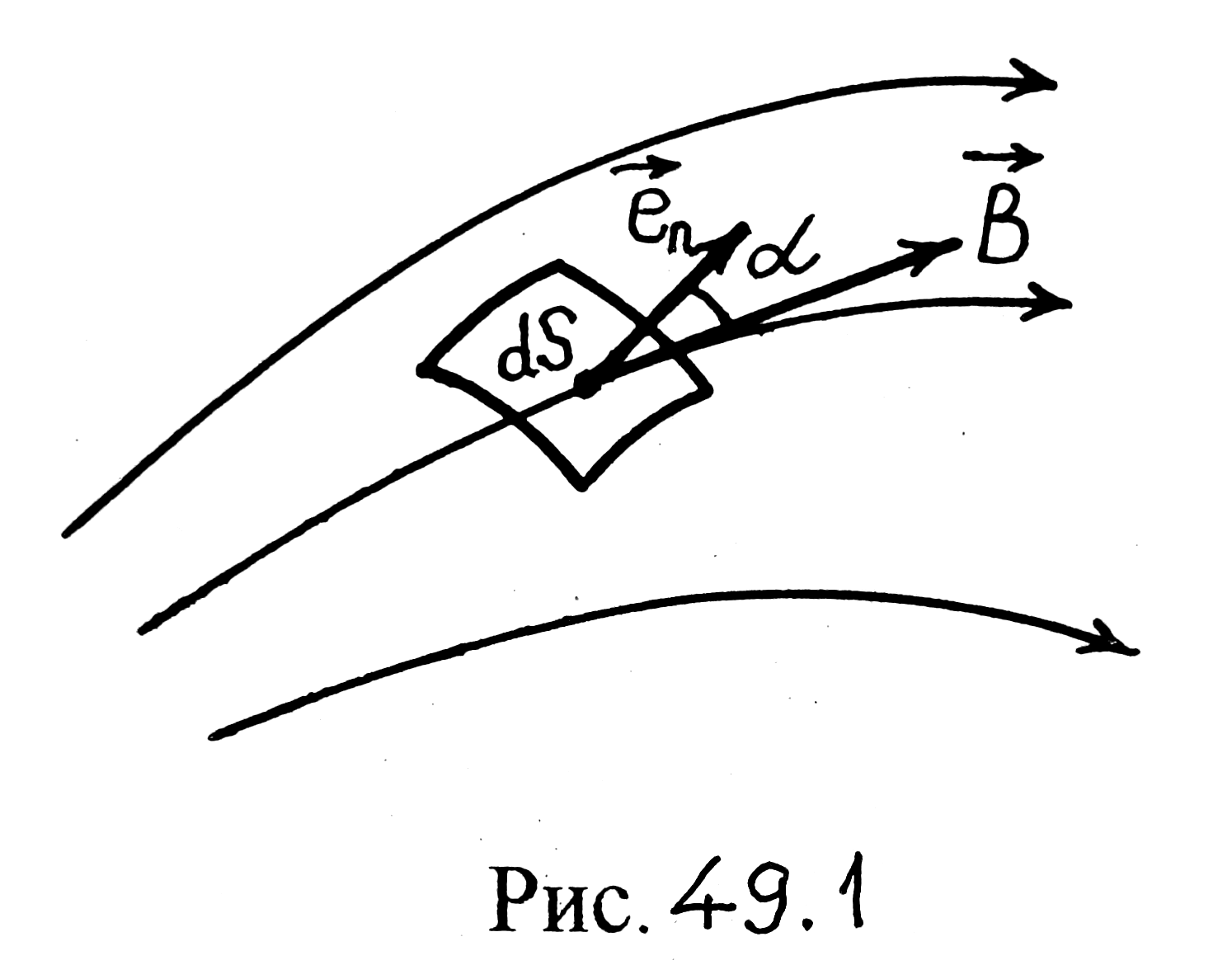
Рис. 49.1
Пусть
— единичный вектор нормали к площадке
dS,
α — угол между векторами
и
.
Тогда число линий вектора
,
пронизывающих dS,
равно
где
— вектор, модуль которого равен dS,
а направление совпадает с единичным
вектором
нормали к площадке dS.
Назовем
потоком
Ф вектора
сквозь произвольную поверхность S
число линий вектора
,
пронизывающих эту поверхность. Очевидно,
(49.1)
интегралу
по поверхности S
от скалярного произведения векторов
и
.
Поток — величина алгебраическая. Знак
потока зависит от выбора направления
нормали к dS.
Для замкнутых поверхностей принято
брать внешнюю нормаль. Поток вектора
измеряют в веберах (Вб).
Теорема
Гаусса для поля вектора
.
Поток вектора
сквозь любую замкнутую поверхность S
равен нулю:
(49.2)
Эта
теорема выражает экспериментальный
факт, что линии вектора
не имеют ни начала, ни конца — они
замкнутые. Поэтому число линий вектора
,
выходящих из любого объема, ограниченного
замкнутой поверхностью S,
всегда равно числу линий, входящих в
этот объем (рис.
49.2).
|
Рис. 49.2 |
Это означает, что магнитное поле не имеет источников (магнитных зарядов) в отличие от электростатического поля. Магнитное поле порождают не магнитные заряды (которых в природе нет), а электрические токи.
Следствие теоремы.
Поток вектора
|
сквозь поверхность S,
ограниченную некоторым замкнутым
контуром, не зависит от формы поверхности
S.
Действительно,
так как линии вектора
нигде не прерываются, их число сквозь
S,
ограниченную данным контуром, не должно
зависеть от формы S
(рис. 49.3).
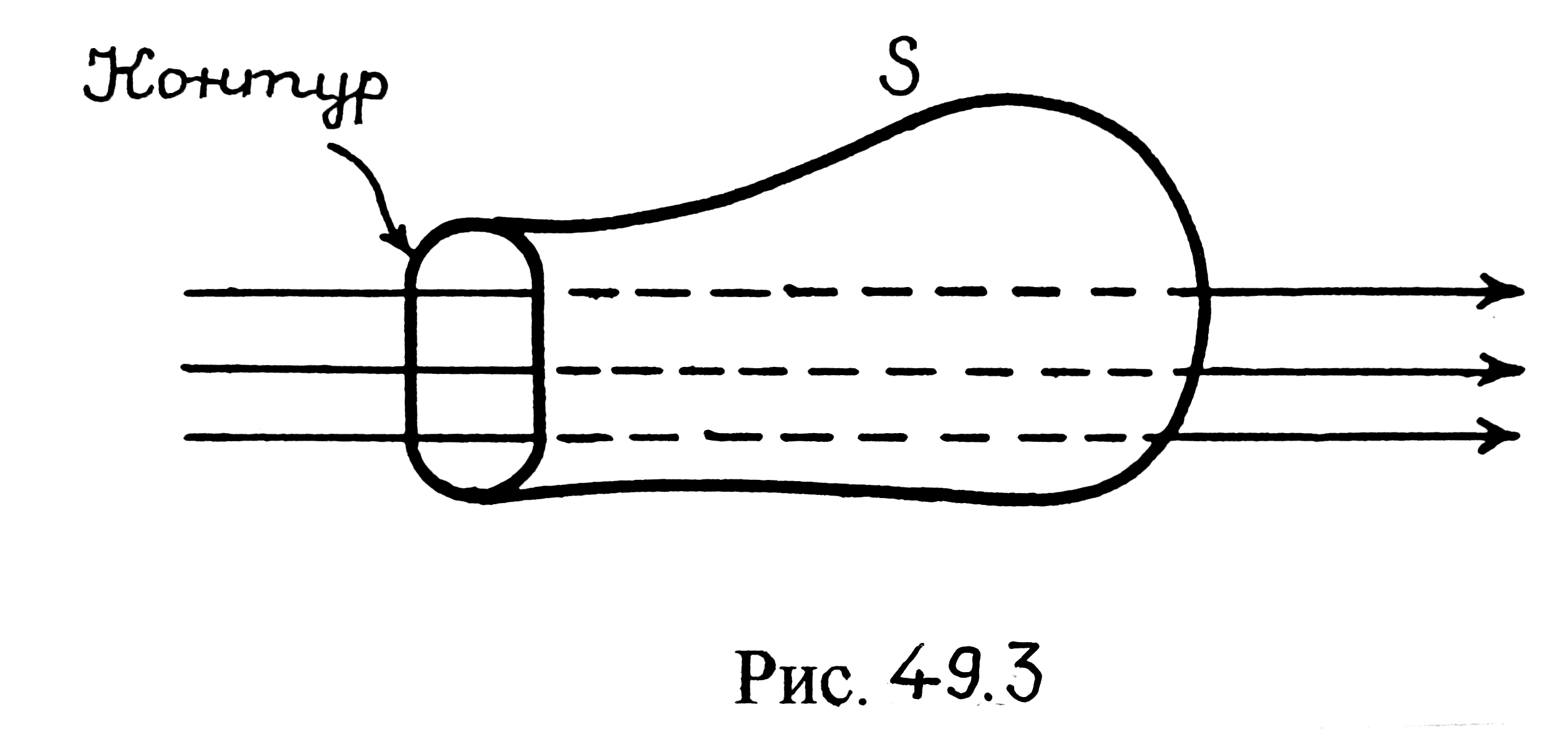
Рис. 49.3