§ 44. Закон Ома для проводника

Ом экспериментально установил закон, согласно которому сила тока, протекающего по металлическому проводнику, пропорциональна разности потенциалов на его концах (напряжению U):

(44.1)

где R — электрическое сопротивление (или просто сопротивление) проводника. Сопротивление измеряют в омах (Ом). Оно зависит от формы и размеров проводника, а также от материала проводника и его температуры.

Сопротивление однородного цилиндрического проводника

(44.2)

где ℓ — длина проводника; S — площадь его поперечного сечения; ρ — коэффициент, называемый удельным электрическим сопротивлением (или просто удельным сопротивлением) проводника. Удельное сопротивление проводника измеряют в ом-метрах (Ом·м). Оно зависит от материала проводника и его температуры.

Величину σ, обратную удельному сопротивлению, называют удельной электрической проводимостью (или просто удельной проводимостью) проводника. Ее измеряют в сименсах на метр (См/м). Сименс — единица измерения, обратная ому (1 См = 1 Ом^–1).

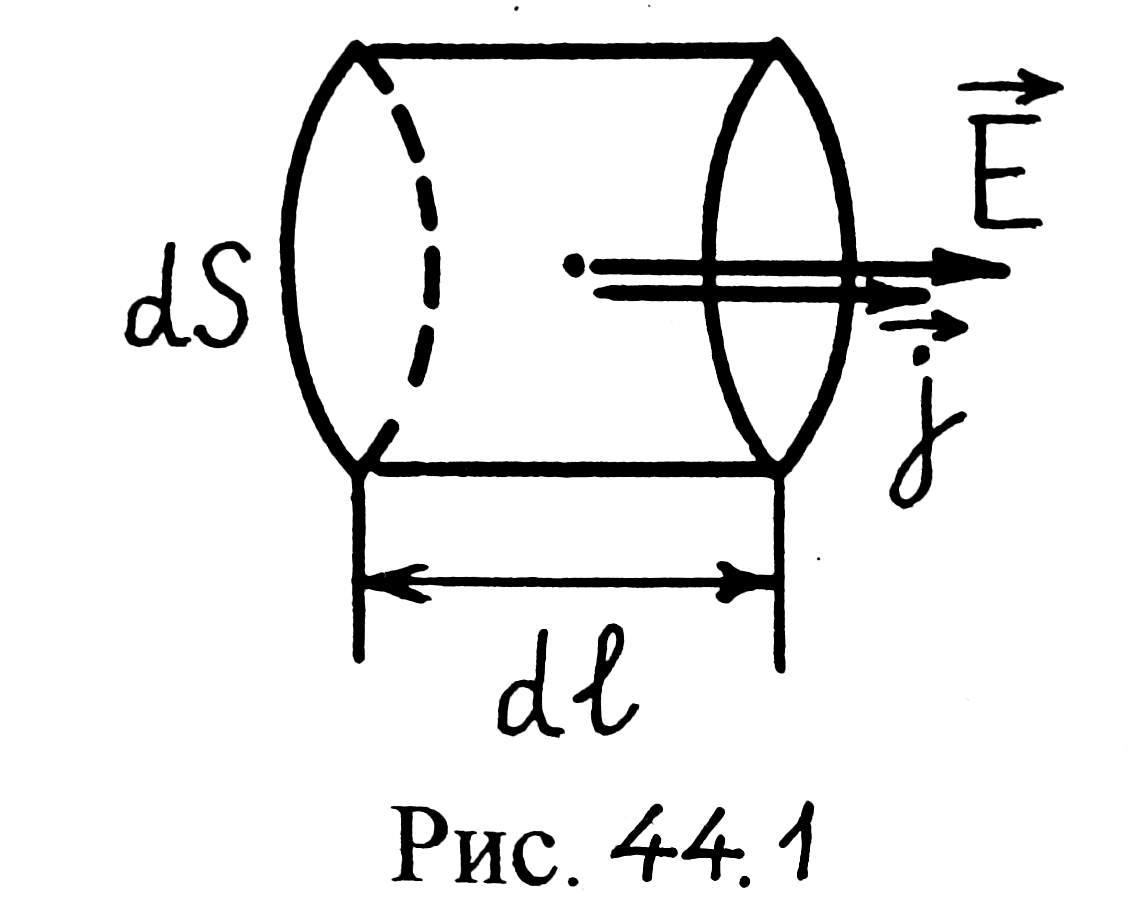
Соотношение (44.1) называют законом Ома для проводника в интегральной форме. Найдем дифференциальную форму этого закона. Для этого выделим мысленно в окрестности некоторой точки проводника элементарный объем в виде цилиндра высотой dℓ и площадью основания dS с образующими, параллельными векторам и в этой точке (рассмотрим изотропный проводник, в котором направления плотности тока и напряженности электрического поля совпадают) (рис. 44.1).

Рис. 44.1

Для такого элементарного цилиндра имеем (44.3) (44.4) (44.5)

Подставляя формулы (44.3)–(44.5) в соотношение (44.1), получаем

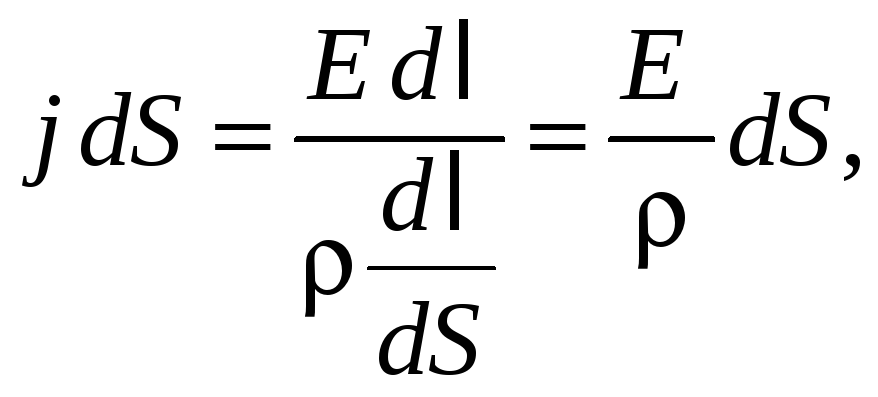
откуда

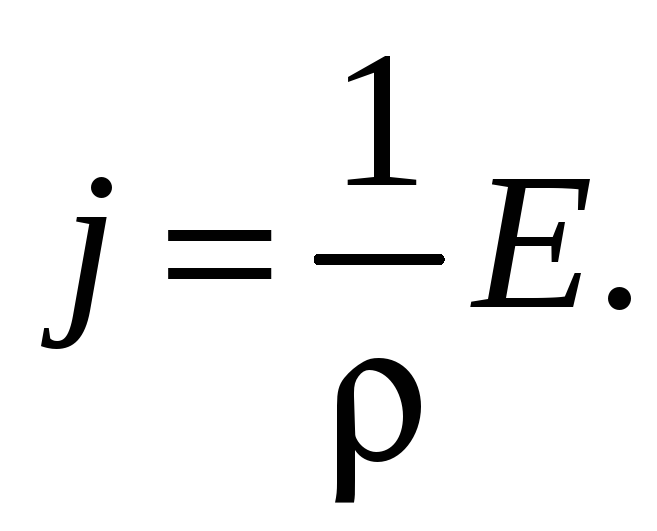
Так как векторы и имеют одинаковое направление, можно написать

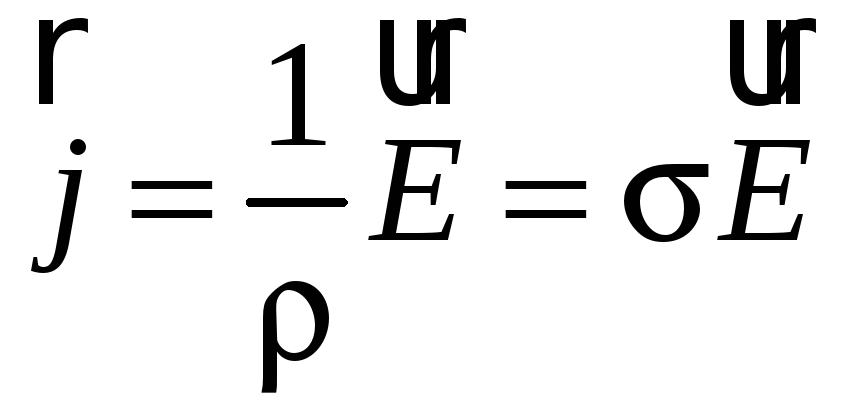(44.6)

— плотность тока в некоторой точке проводника равна произведению удельной проводимости проводника на напряженность электрического поля в этой точке (закон Ома для проводника в дифференциальной форме).

§ 45. Обобщенный закон Ома

Заряженные частицы движутся в проводнике под действием сил электростатического поля, обусловленного избытком одноименно заряженных частиц на одном конце проводника по отношению к другому. В конечном счете это ведет к выравниванию количеств одноименно заряженных частиц на концах проводника и прекращению электрического тока. Чтобы поддержать постоянный ток в проводнике, необходимо постоянно переносить заряженные частицы в обратном направлении против сил электрического поля. Устройство, которое этот перенос осуществляет, называют источником постоянного тока. Перенос заряженных частиц в источнике тока возможен лишь с помощью сил неэлектростатического происхождения. Такие силы называют сторонними. Для количественной характеристики сторонних сил вводят понятие поля сторонних сил и его напряженность . Напряженность определяют как стороннюю силу, действующую на единичный положительный точечный заряд в данной точке поля сторонних сил.

Для электрической цепи, состоящей из проводника и источника постоянного тока (рис. 45.1), можем написать (см. выражение (44.6)):

(45.1)

— плотность тока в некоторой точке проводника в цепи, содержащей источник постоянного тока, равна произведению удельной проводимости проводника на сумму напряженностей электрического поля и поля сторонних сил в этой точке (обобщенный закон Ома в дифференциальной форме).

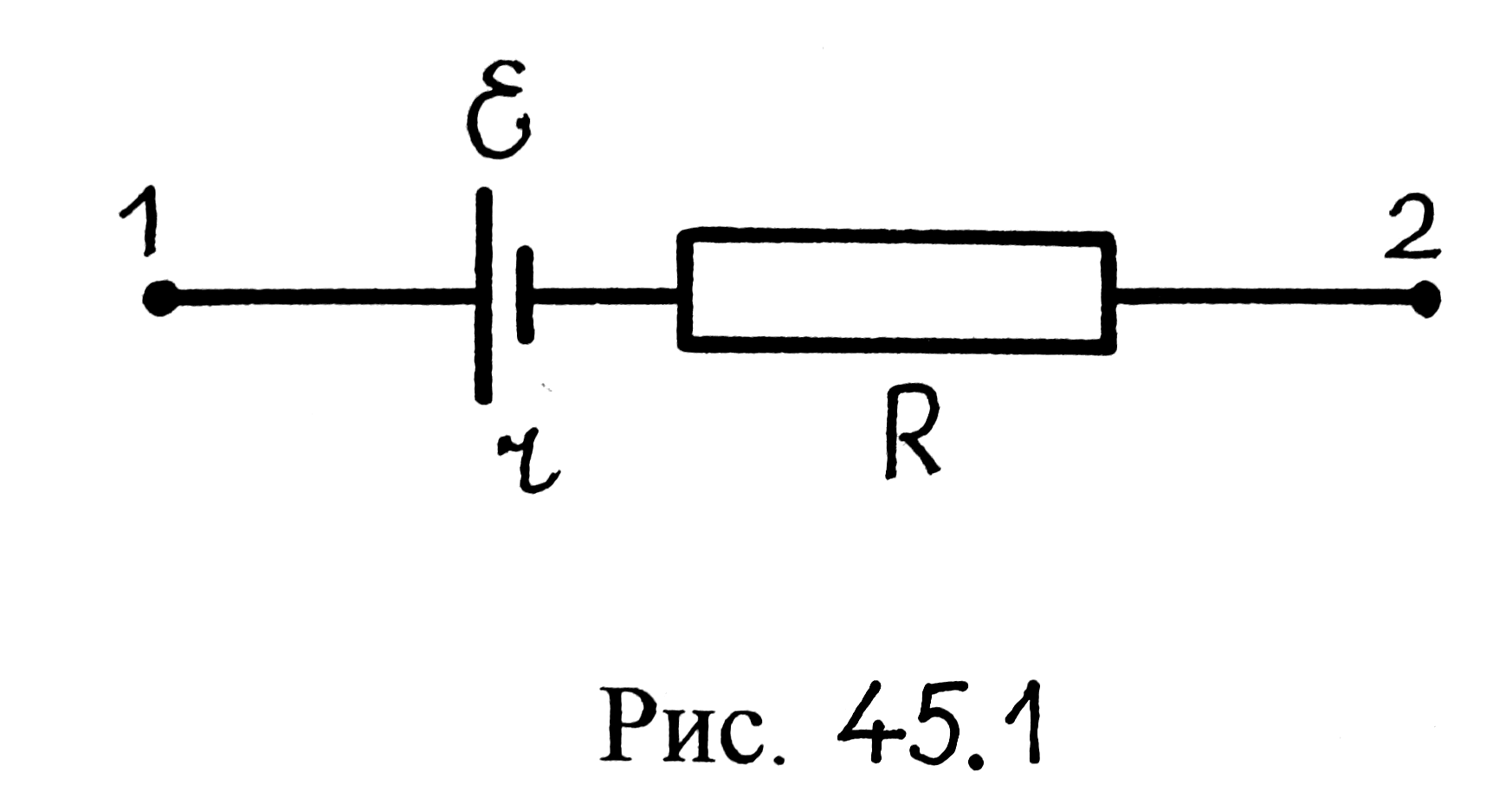
Рис. 45.1

Найдем интегральную форму обобщенного закона Ома. Пусть — элементарное перемещение вдоль электрической цепи по направлению линий вектора . Из соотношения (45.1) следует

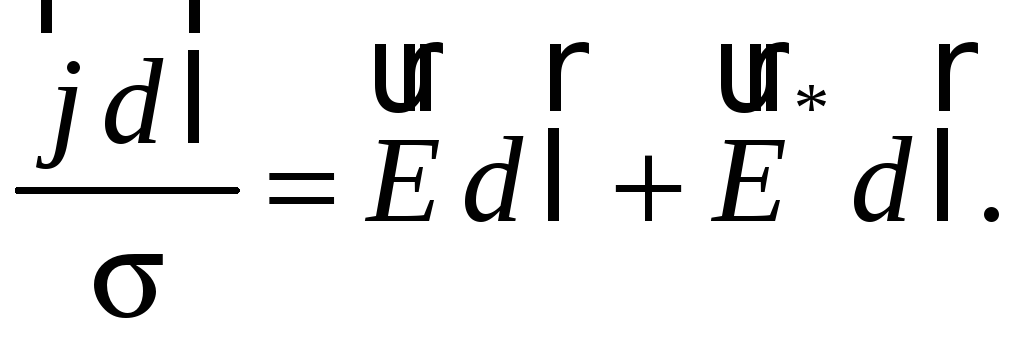(45.2)

Проинтегрируем выражение (45.2) по всей длине электрической цепи от точки 1 до точки 2 (см. рис. 45.1):

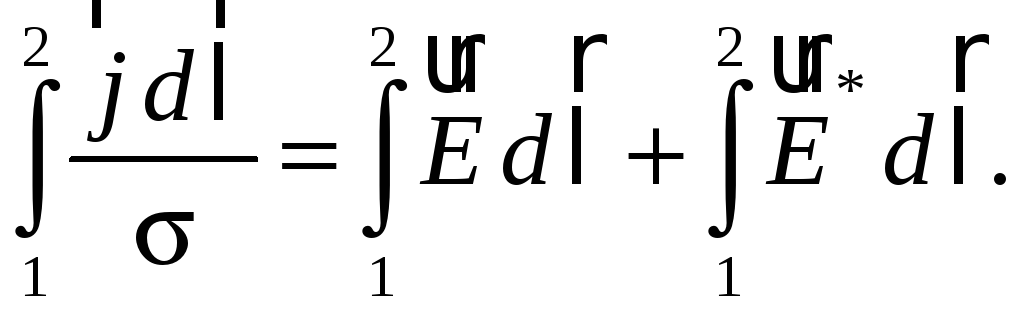(45.3)

В соотношении (45.3)

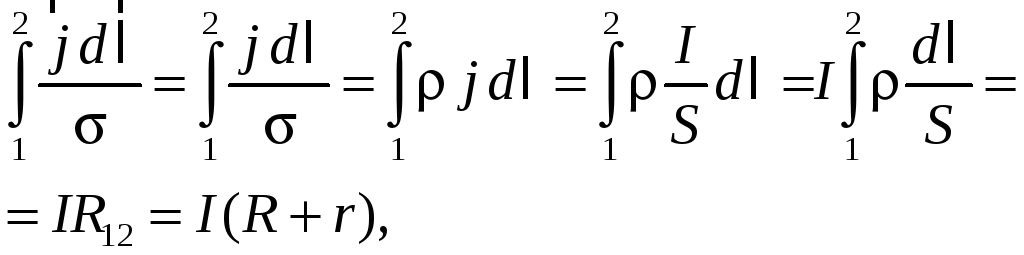(45.4)

где R — сопротивление проводника (внешнее сопротивление); r — сопротивление источника тока (внутреннее сопротивление),

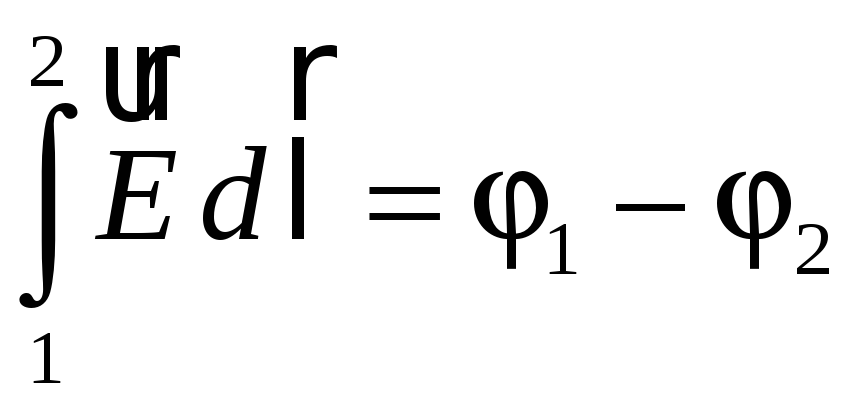(45.5)

— разность потенциалов между точками 1 и 2 цепи,

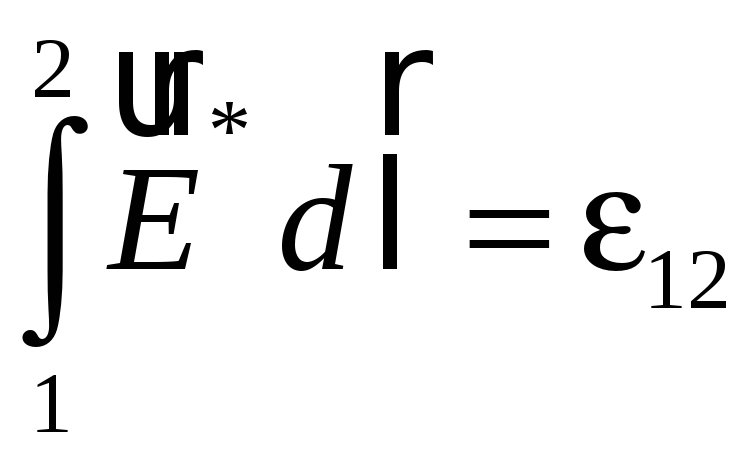(45.6)

— электродвижущая сила (эдс) источника тока, действующего между точками 1 и 2 цепи. Можно сказать, что электродвижущая сила ε₁₂ численно равна работе, совершаемой сторонними силами при перемещении единичного положительного точечного заряда по цепи между точками 1 и 2.

Подставляя формулы (45.4)–(45.6) в соотношение (45.3), получаем

откуда

(45.7)

— сила тока, протекающего по проводнику в цепи, содержащей источник постоянного тока, пропорциональна сумме разности потенциалов между концами этой цепи и электродвижущей силы источника тока в этой цепи (обобщенный закон Ома в интегральной форме).

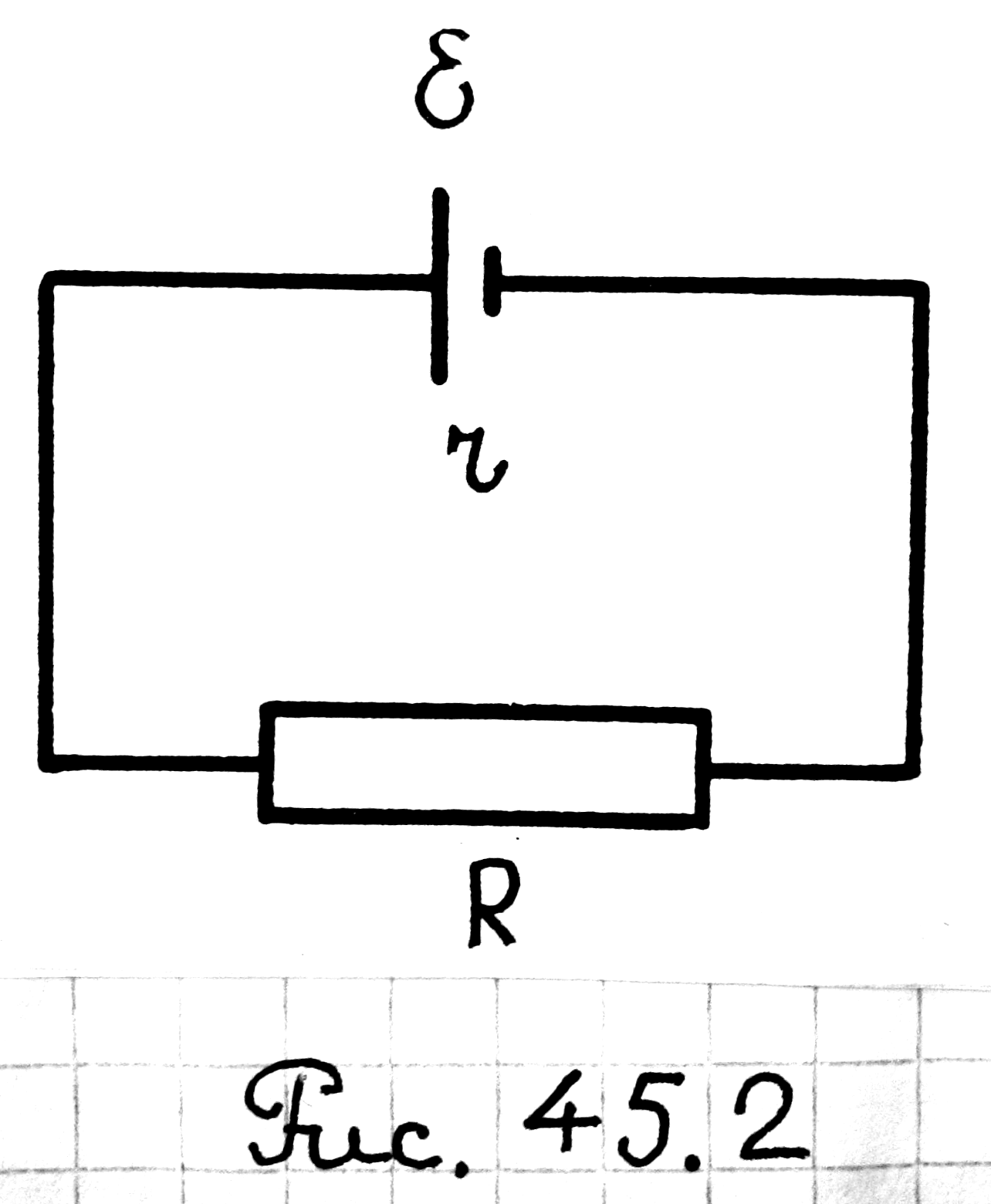
Для замкнутой электрической цепи (рис. 45.2) имеем . Из обобщенного закона Ома (45.7) следует

(45.8)

Рис. 45.2

Отметим, что в случае нескольких источников тока в электрической цепи в выражениях (45.7) и (45.8) — алгебраической сумме эдс источников тока (, если эдс способствует движению положительных носителей тока, , если препятствует).