§ 42. Энергия электрического поля

Имеем заряженный проводник. Увеличим его заряд на dq. Для этого надо совершить работу против сил электрического поля (одноименные заряды отталкиваются). Работа, совершаемая внешними силами при переносе заряда dq из бесконечности на проводник,

(42.1)

где φ — потенциал проводника (мы приняли потенциал на бесконечности ).

Для увеличения заряда проводника на q надо совершить работу

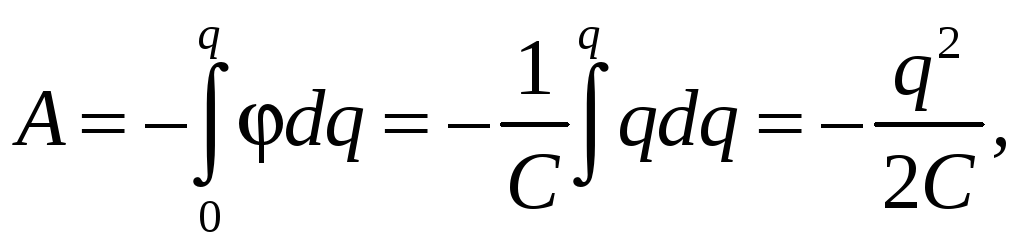(42.2)

где C — электроемкость проводника (см. формулу (40.4)). Знак минус указывает, что работа совершается против сил электрического поля. При разряде проводника работа совершается уже силами электрического поля, поэтому эту работу записывают со знаком плюс. Так как совершенная при разряде проводника работа равна сообщенной проводнику энергии, то

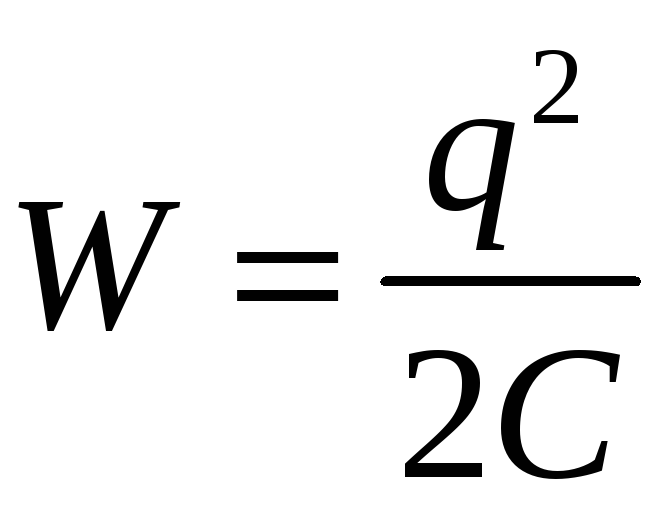(42.3)

есть электрическая энергия заряженного проводника.

Получим выражение для электрической энергии плоского конденсатора. С учетом выражений (41.7) и (41.9) перепишем формулу (42.3) в виде

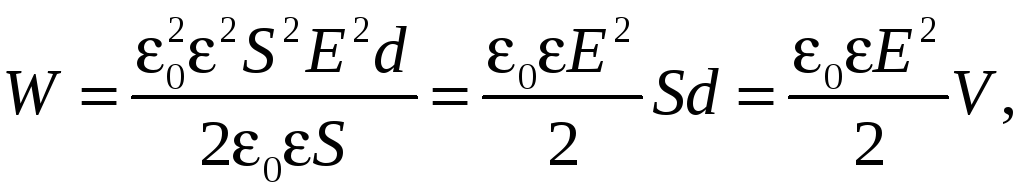(42.4)

где — объем между обкладками конденсатора.

Так как электрическое поле, создаваемое конденсатором, практически полностью сосредоточено между его обкладками, то выражение (42.4) определяет энергию электрического поля в объеме V. Разделив W на V, получим объемную плотность энергии электрического поля:

(42.5)

Формула (42.5) справедлива не только для поля плоского конденсатора, но и для любого электрического поля. Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объеме V:

(42.6)

Глава 12. Электрический ток § 43. Электрический ток

Назовем электрическим током (или просто током) упорядоченный перенос заряженных частиц (носителей тока) через какую-либо поверхность S. Перенос заряженных частиц происходит под действием электрического поля. Следовательно, для электрического тока необходимы заряженные частицы и электрическое поле. Например, заряженные частицы — электроны — в тонком длинном цилиндрическом металлическом проводнике (электрическом проводе) переносятся в одном направлении по проводнику, если между его концами создать разность потенциалов . Отметим, что средняя скорость упорядоченного движения электронов в электрическом проводе ничтожно мала по сравнению со средней скоростью их теплового движения и не превышает 1 мм/с.

За направление тока условились принимать направление движения положительно заряженных частиц. Следовательно, в металлическом проводнике направление тока противоположно направлению движения электронов.

Количественной характеристикой тока является сила тока. Сила тока — это скалярная величина.

(43.1)

где dq — заряд, переносимый через поверхность S за элементарный (очень малый) промежуток времени dt. Силу тока измеряют в амперах (А).

Электрический ток называют постоянным, если его направление и сила тока не изменяются с течением времени. В дальнейшем мы будем рассматривать постоянный ток. Однако отметим, что все законы постоянного тока, которые сформулируем, можно применять и для тока, сила которого изменяется не слишком быстро со временем (квазистационарного тока).

Электрический ток может быть распределен по поверхности S неравномерно. Поэтому вводят понятие плотности тока . Плотность тока — это вектор, направление которого совпадает с направлением электрического тока, а модуль

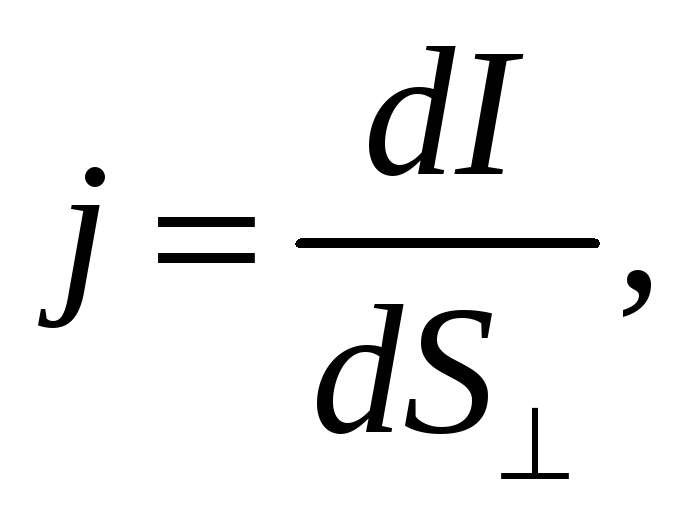(43.2)

где dI — сила тока через элементарную площадку , расположенную в данной точке перпендикулярно направлению тока.

В металлических проводниках плотность тока

(43.3)

где ρ и — объемная плотность и средняя скорость упорядоченного движения носителей тока (электронов) (ρ < 0, поэтому направления векторов и противоположны)

Поле вектора можно изобразить наглядно с помощью линий вектора , которые проводят аналогично линиям вектора (см. § 32).

Возьмем любую элементарную площадку dS поверхности S. Пусть  — единичный вектор нормали к площадке dS; α — угол между векторами и .Тогда с учетом выражения (43.2) можем написать

(43.4)

где Зная в каждой точке S, можно найти силу I тока сквозь S:

(43.5)

Следовательно, сила электрического тока через поверхность S равна потоку плотности тока сквозь эту поверхность. Опыт показывает, что для постоянного тока по всему поперечному сечению S однородного проводника, и поэтому

(43.6)

Пусть S — замкнутая поверхность, а векторы проведены по внешним нормалям к поверхности. Тогда поток вектора сквозь поверхность S равен силе I тока, текущего из области, ограниченной S, наружу. Электрический заряд q, охватываемый поверхностью S, уменьшается за время dt на т. е.

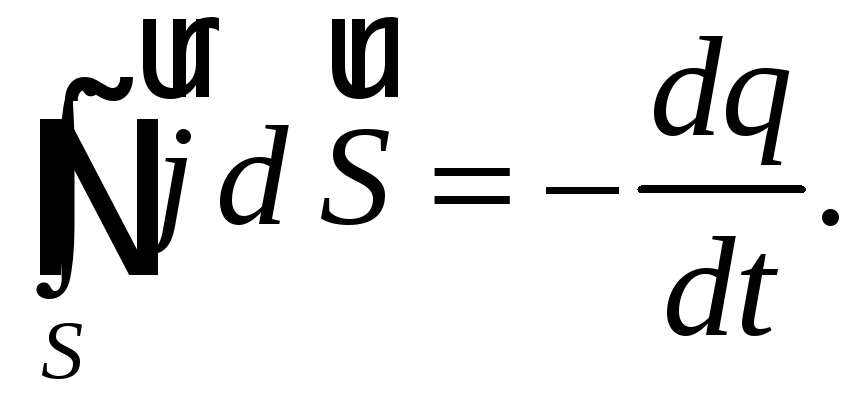
Соотношение (43.7) называют уравнением непрерывности.

Пример 43.1. Какой заряд q пройдет по проводнику за промежуток времени если сила тока за это время равномерно убывает от до ?

Дано:	Решение . Согласно условию задачи, где коэффициент k определяет скорость убывания силы тока.
q – ?

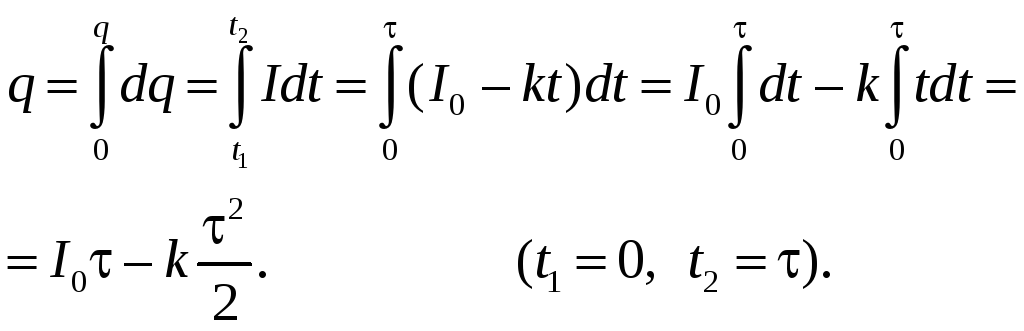
Ответ: