
- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
Глава 11. Энергия электрического поля § 40. Электроемкость
Рассмотрим металлический шар, окруженный средой с диэлектрической проницаемостью ε.
Металлический
шар представляет собой проводник, в
котором могут свободно перемещаться
заряженные частицы — электроны. Если
шару сообщить заряд q
(добавить или убрать некоторое количество
электронов), то электроны в шаре
распределятся так, чтобы соблюдалось
условие равновесия, а именно, чтобы
напряженность
![]() электрического поля внутри шара равнялась
нулю. Это условие будет выполняться при
равномерном распределении заряда q
по поверхности шара (см. пример 33.2).
Следовательно, металлический заряженный
шар эквивалентен равномерно заряженной
сфере. Потенциал φ внутри металлического
шара везде одинаков и равен потенциалу
на поверхности шара (см. пример 39.1):
электрического поля внутри шара равнялась
нулю. Это условие будет выполняться при
равномерном распределении заряда q
по поверхности шара (см. пример 33.2).
Следовательно, металлический заряженный
шар эквивалентен равномерно заряженной
сфере. Потенциал φ внутри металлического
шара везде одинаков и равен потенциалу
на поверхности шара (см. пример 39.1):
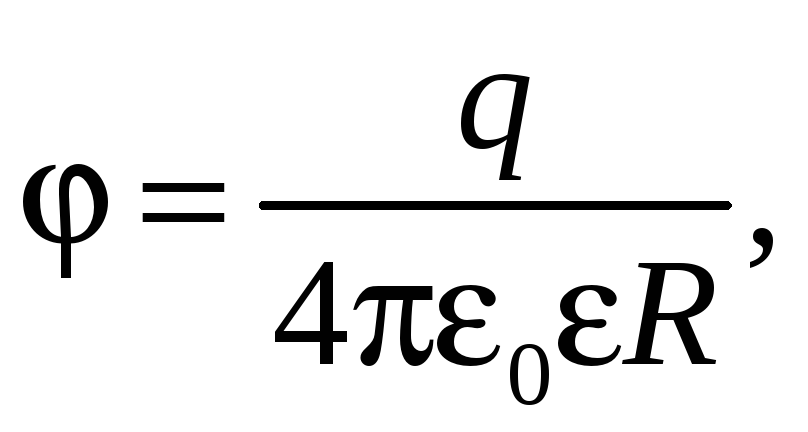 (40.1)
(40.1)
где R — радиус шара.
Перепишем соотношение (40.1) в виде
![]() (40.2)
(40.2)
где
![]() (40.3)
(40.3)
— коэффициент пропорциональности между зарядом и потенциалом шара — называют электрической емкостью (или просто электроемкостью) металлического шара.
Из выражения (40.3) видно, что электроемкость шара зависит от размеров шара (радиус R) и диэлектрических свойств окружающей среды (диэлектрической проницаемости ε). Очевидно, для проводника другой формы (например, для металлического цилиндра) коэффициент пропорциональности в соотношении (40.2) будет иметь другой вид, чем (40.3).
Обобщая, можно сказать, что электроемкость проводника
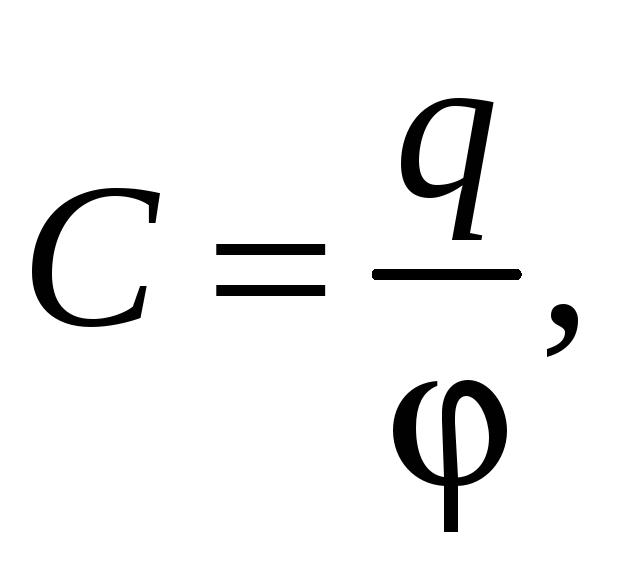 (40.4)
(40.4)
заряду, который нужно сообщить проводнику, чтобы увеличить его потенциал на 1 В. Электроемкость зависит от формы и размеров проводника, а также от диэлектрических свойств окружающей среды. Единицей измерения электроемкости является фарад (Ф)
Если к заряженному проводнику, например, с q > 0, поднести незаряженный проводник, то на незаряженном проводнике произойдет перераспределение зарядов — в данном случае отрицательные заряды сместятся относительно положительных в сторону заряженного проводника. Вследствие этого потенциал заряженного проводника уменьшится, что приведет к увеличению его электроемкости (см. формулу (40.4)). Значительное увеличение электроемкости произойдет, если к положительно заряженному проводнику поднести отрицательно заряженный проводник. Систему из двух проводников (обкладок), имеющих противоположные по знаку, но равные по величине заряды, называют конденсатором. Форма и взаимное расположение обкладок конденсатора таковы, что электрическое поле, создаваемое конденсатором, практически полностью сосредоточено между его обкладками. Электроемкость конденсатора
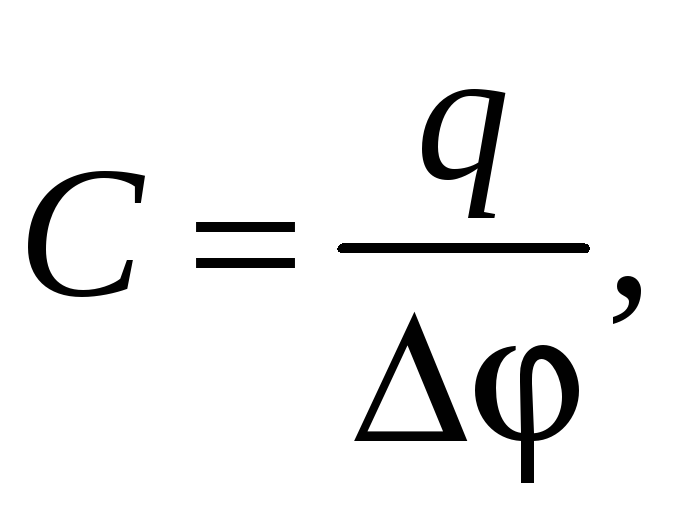 (40.5)
(40.5)
где
q
— заряд положительно заряженной
обкладки;
![]() — разность потенциалов между обкладками.
Электроемкость конденсатора зависит
от формы и размеров обкладок, от расстояния
между ними, а также от диэлектрических
свойств среды, заполняющей конденсатор.
Электроемкость является основной
характеристикой конденсатора.
— разность потенциалов между обкладками.
Электроемкость конденсатора зависит
от формы и размеров обкладок, от расстояния
между ними, а также от диэлектрических
свойств среды, заполняющей конденсатор.
Электроемкость является основной
характеристикой конденсатора.
§ 41. Электроемкость плоского конденсатора
Найдем электроемкость плоского конденсатора. Плоский конденсатор состоит из двух параллельных металлических пластин (обкладок) площадью S каждая, расположенных на близком расстоянии d одна от другой. Заряды пластин +q и – q. Пространство между пластинами заполнено средой с диэлектрической проницаемостью ε (рис. 41.1).
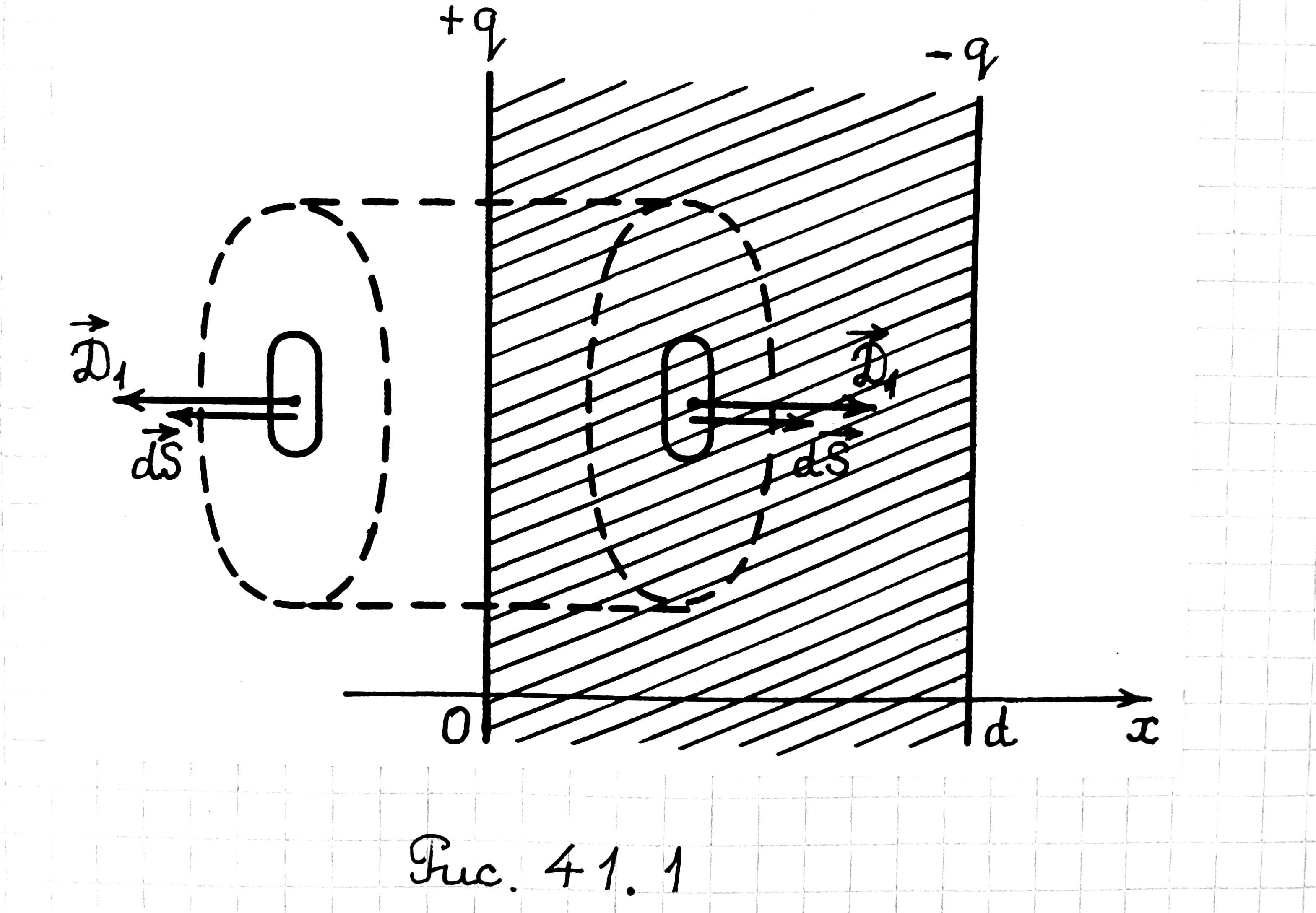
Рис. 41.1
Для
нахождения разности потенциалов Δφ
между пластинами конденсатора
воспользуемся соотношением (36.7). Получим
выражение для напряженности E
электрического поля в конденсаторе.
Возьмем любую точку между пластинами
конденсатора. Вследствие симметрии
(заряд каждой пластины равномерно
распределяется по поверхности пластины
(см. пример 33.1)) вектор
![]() поля, создаваемого левой пластиной, в
этой точке направлен по оси x.
Определим модуль (длину) этого вектора.
Проведем через интересующую нас точку
гауссову замкнутую поверхность S
в виде симметричного относительно левой
пластины цилиндра так, чтобы точка
находилась на основании цилиндра (рис.
41.1). Найдем
поток вектора
поля, создаваемого левой пластиной, в
этой точке направлен по оси x.
Определим модуль (длину) этого вектора.
Проведем через интересующую нас точку
гауссову замкнутую поверхность S
в виде симметричного относительно левой
пластины цилиндра так, чтобы точка
находилась на основании цилиндра (рис.
41.1). Найдем
поток вектора
![]() сквозь гауссову поверхность:
сквозь гауссову поверхность:
![]() (41.1)
(41.1)
где
Sосн
— площадь основания цилиндра. При
интегрировании мы учли, что поток вектора
![]() сквозь боковую поверхность цилиндра
равен нулю (линии вектора
сквозь боковую поверхность цилиндра
равен нулю (линии вектора
![]() не пронизывают эту поверхность) и для
всех точек основания цилиндра α = 0
и D1
= const.
не пронизывают эту поверхность) и для
всех точек основания цилиндра α = 0
и D1
= const.
Согласно теореме Гаусса
![]() (41.2)
(41.2)
где
![]() — заряд пластины, сосредоточенный
внутри цилиндра. Можем написать
— заряд пластины, сосредоточенный
внутри цилиндра. Можем написать
![]() (41.3)
(41.3)
(мы
учли, что поверхностная плотность заряда
![]() где q
и S
— заряд и площадь пластины).
где q
и S
— заряд и площадь пластины).
Подставляя выражения (41.1) и (41.3) в соотношение (41.2), получаем
![]()
откуда
![]() (41.4)
(41.4)
Аналогично
можно определить модуль вектора
![]() в той же точке электрического поля,
создаваемого правой пластиной. Расчет
дает
в той же точке электрического поля,
создаваемого правой пластиной. Расчет
дает
![]() (41.5)
(41.5)
Очевидно, внутри конденсатора
![]()
![]() (41.6)
(41.6)
Воспользовавшись соотношением (39.8), находим напряженность E:
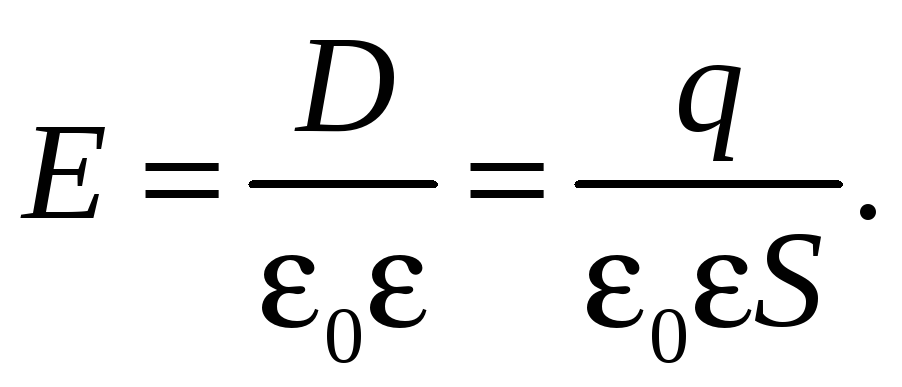 (41.7)
(41.7)
Подставим выражение (41.7) в соотношение (36.7) и проинтегрируем:
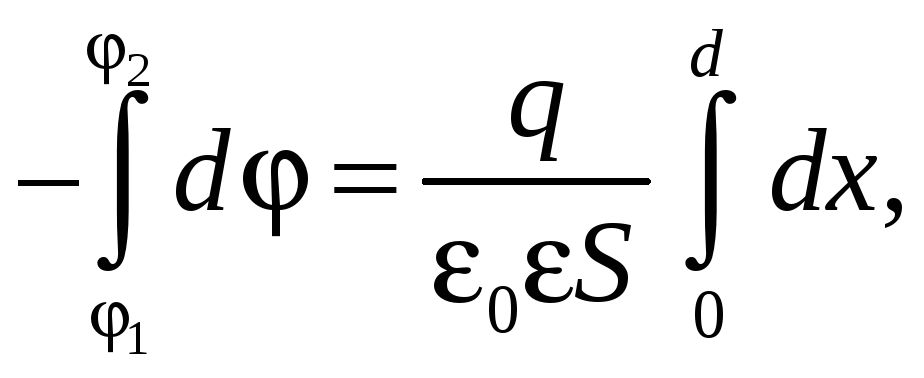
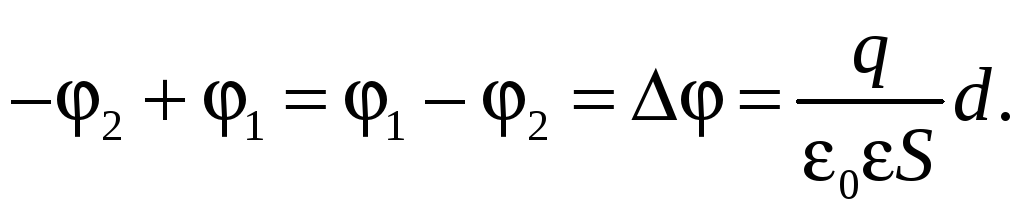 (41.8)
(41.8)
Подставляя формулу (41.8) в выражение (40.5), получаем электроемкость плоского конденсатора
![]() (41.9)
(41.9)
