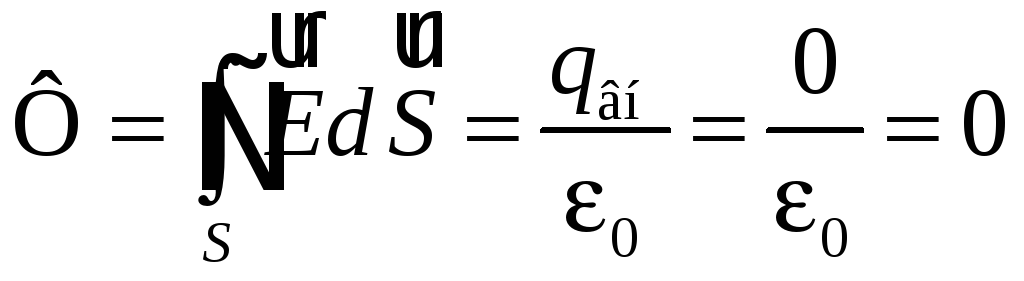§ 32. Поток вектора

Наглядно поле вектора изображают с помощью линий вектора , которые проводят следующим образом:

1. касательная к ним в каждой точке совпадает с направлением вектора ;

2. число линий, пронизывающих единицу площади поверхности, перпендикулярную линиям (густота линий), равно модулю вектора 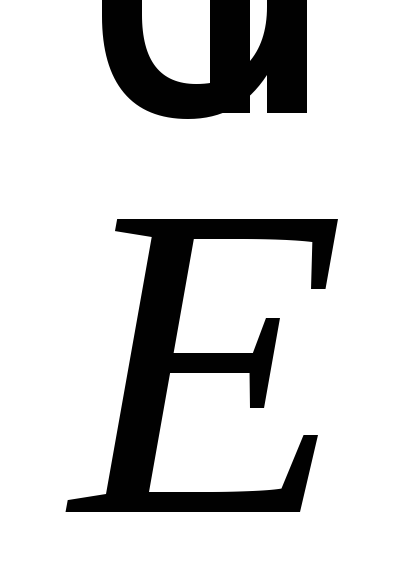(рис. 32.1).

Электрическое поле называют однородным, если в каждой точке поля вектор = const. Линии вектора такого поля параллельны и расстояния между ними одинаковы (рис. 32.2).

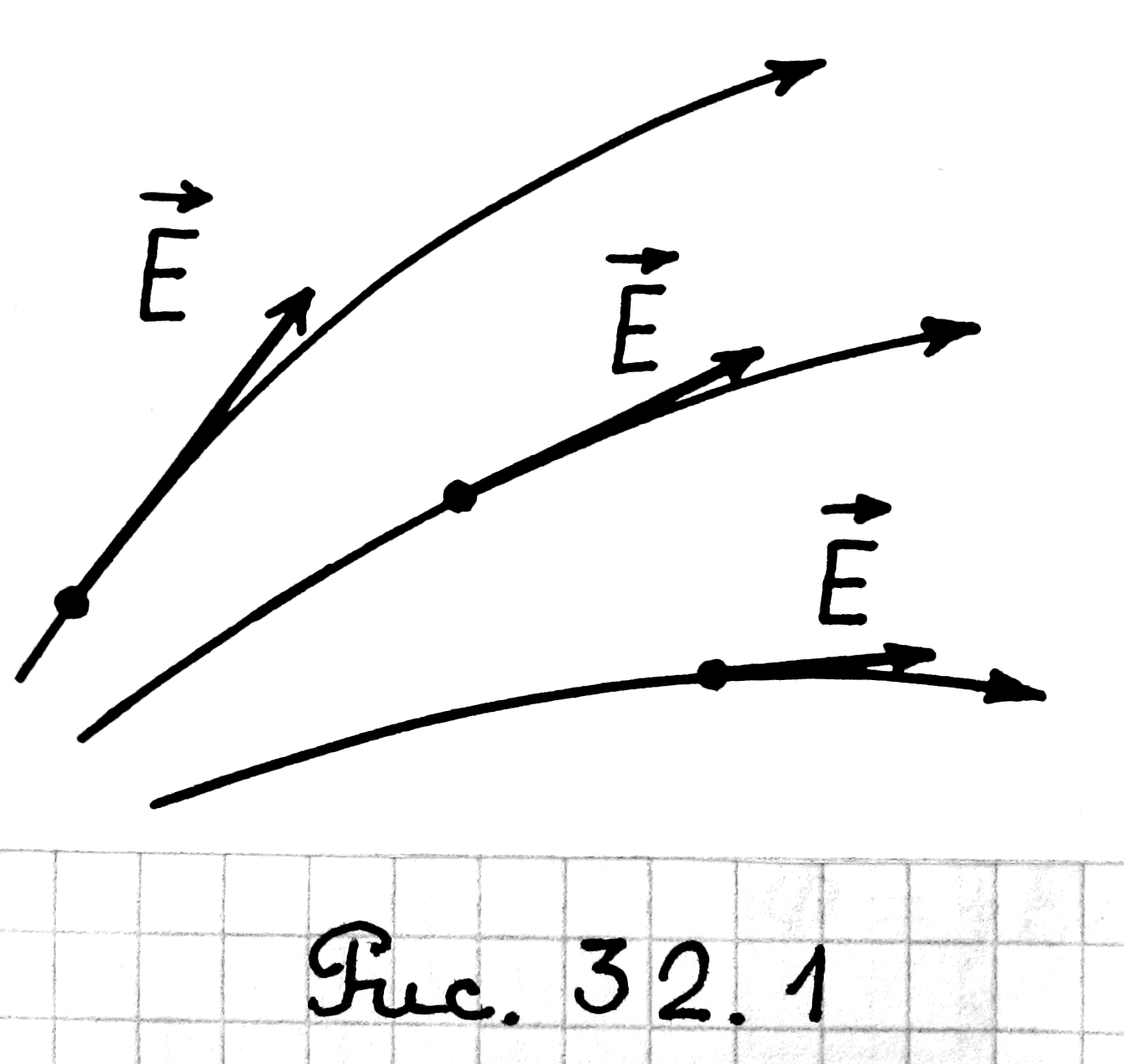
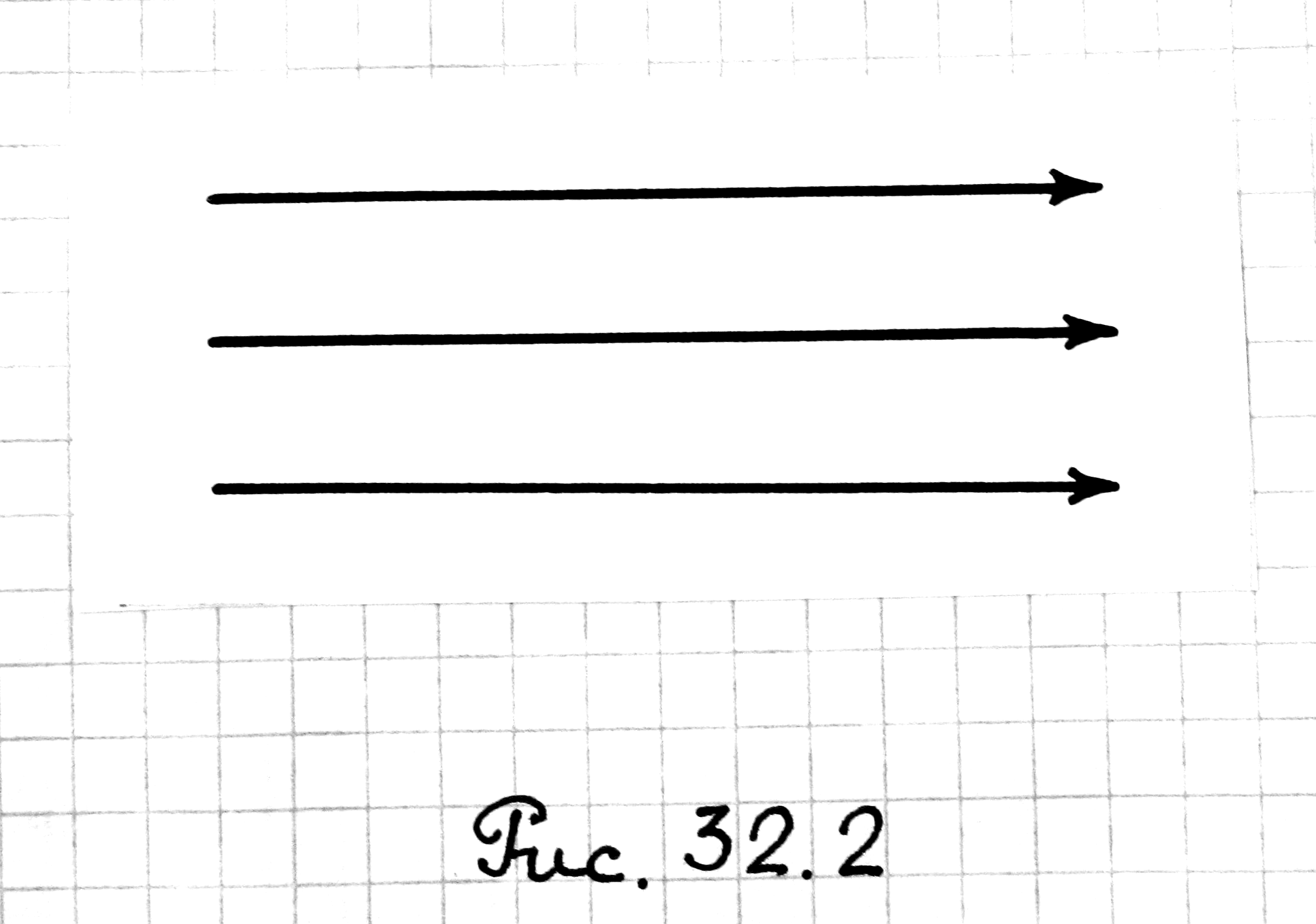
Рис. 32.1 Рис. 32.2

Линии вектора электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах.

Возьмем элементарную площадку dS в поле вектора (рис. 32.3). Пусть — единичный вектор нормали к площадке dS, α — угол между векторами и . Тогда число линий вектора , пронизывающих dS, равно

где — вектор, модуль которого равен dS, а направление совпадает с единичным вектором нормали к площадке dS.

Рис. 32.3

Назовем потоком Ф вектора сквозь произвольную поверхность S число линий вектора , пронизывающих эту поверхность. Очевидно,

интегралу по поверхности S от скалярного произведения векторов и . Поток — величина алгебраическая. Знак потока зависит от выбора направления нормали к dS. Для замкнутых поверхностей принято брать внешнюю нормаль.

§ 33. Теорема Гаусса для поля вектора

Теорема. Поток вектора сквозь любую замкнутую поверхность S равен q_вн/ε₀, где q_вн — алгебраическая сумма зарядов внутри этой поверхности:

(33.1)

где кружок у интеграла означает, что интегрирование проводится по замкнутой поверхности.

Доказательство теоремы. Рассмотрим электрическое поле одного неподвижного точечного заряда q. Пусть q > 0. Мысленно окружим заряд q произвольной замкнутой поверхностью S (рис. 33.1).

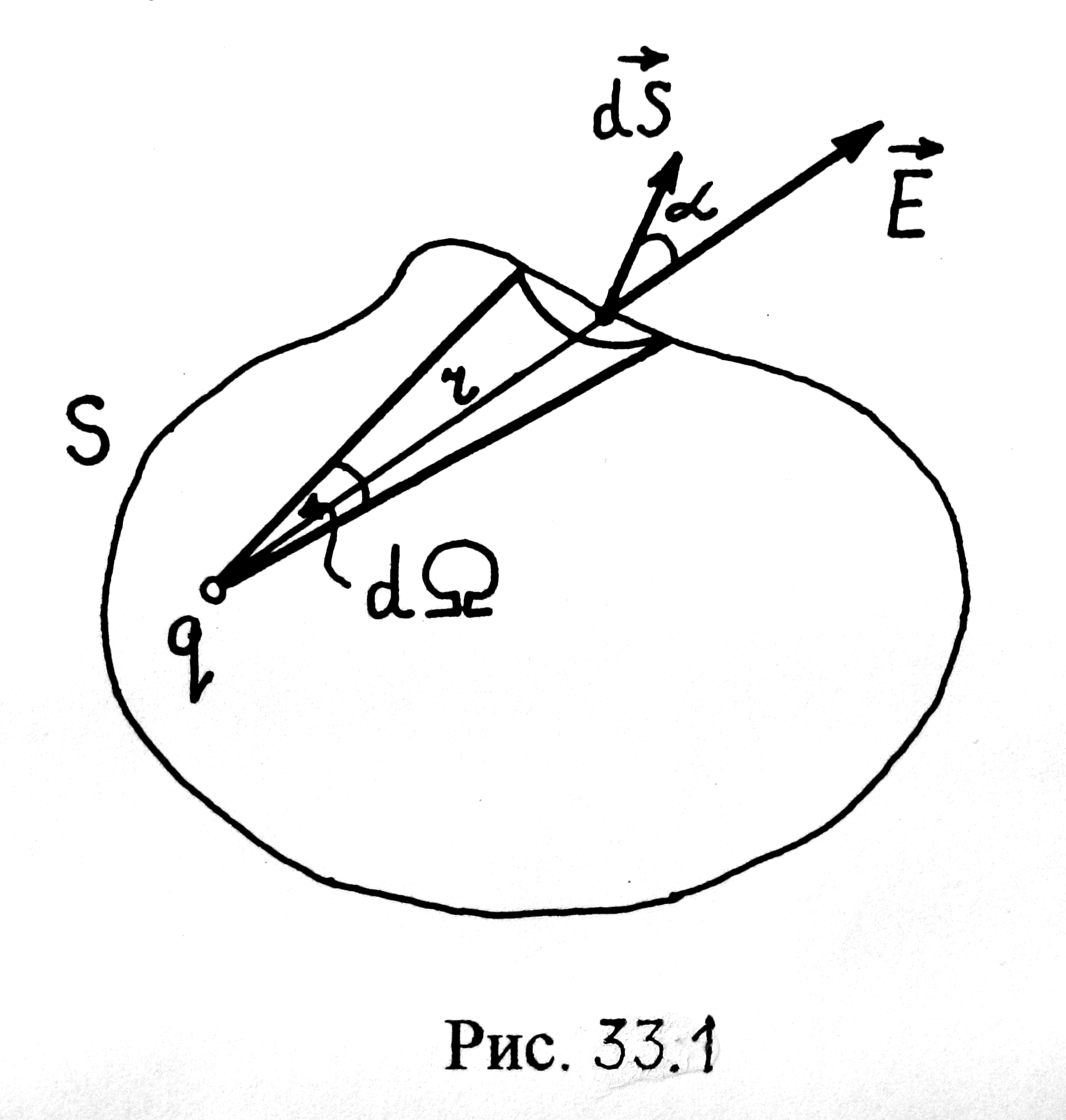
Рис. 33.1

Найдем поток dФ вектора сквозь элемент dS поверхности. Очевидно,

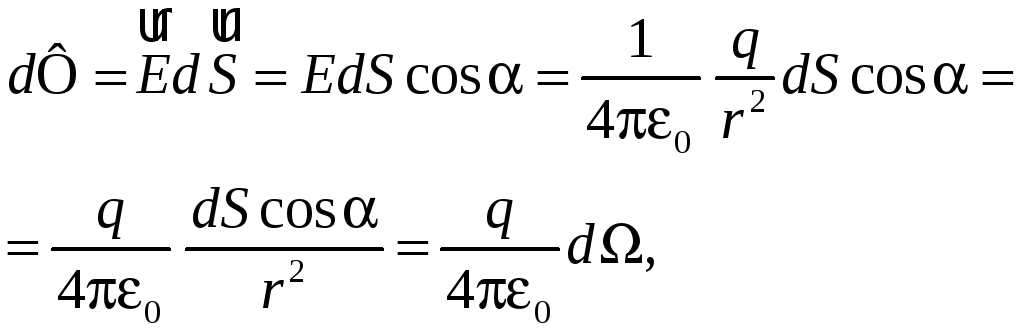
где — элементарный телесный (пространственный) угол внутри конуса, опирающегося на dS, с вершиной в точке расположения заряда q.

Поток вектора сквозь всю замкнутую поверхность S

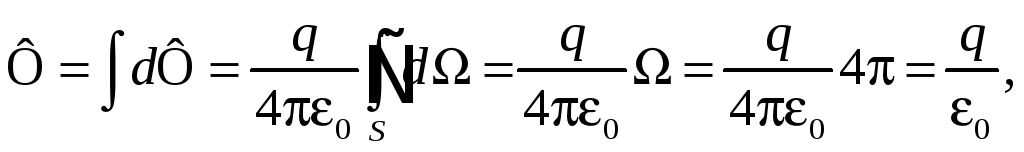
где — полный телесный угол. Мы получили

что совпадает с выражением (33.1).

Теперь рассмотрим электрическое поле, создаваемое системой N неподвижных точечных зарядов Мысленно окружим эту систему зарядов произвольной замкнутой поверхностью S. Используя принцип суперпозиции электрических полей, можем написать

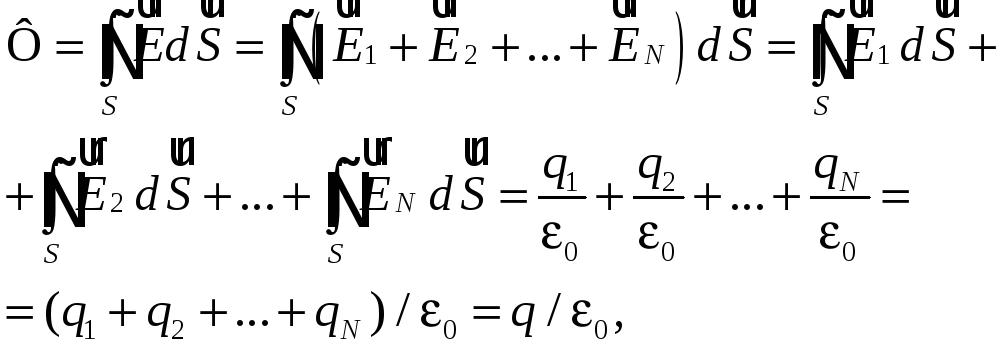
где q — алгебраическая сумма N зарядов, что совпадает с выражением (33.1).

Теорема Гаусса позволяет в некоторых случаях очень просто определить напряженность в любой точке электрического поля.

Пример 33.1. Имеем бесконечную равномерно заряженную плоскость с поверхностной плотностью заряда σ. Определить напряженность Е электрического поля на расстоянии x от плоскости.

Дано: σ x	Решение Проведем ось x, как показано на рис. 33.2 (перпендикулярно плоскости слева направо). Пусть плоскость заряжена положительно. Вследствие симметрии вектор поля, создаваемого плоскостью, в интересующей нас точке направлен по оси x. Определим модуль (длину) этого вектора.
E – ?

Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде симметричного относительно плоскости цилиндра так, чтобы точка находилась на основании цилиндра (рис. 32.2). Найдем поток вектора сквозь гауссову поверхность:

(33.2)

где S_осн — площадь основания цилиндра. При интегрировании мы учли, что поток вектора сквозь боковую поверхность цилиндра равен нулю (линии вектора не пронизывают эту поверхность) и для всех точек основания цилиндра α = 0 и Е = const.

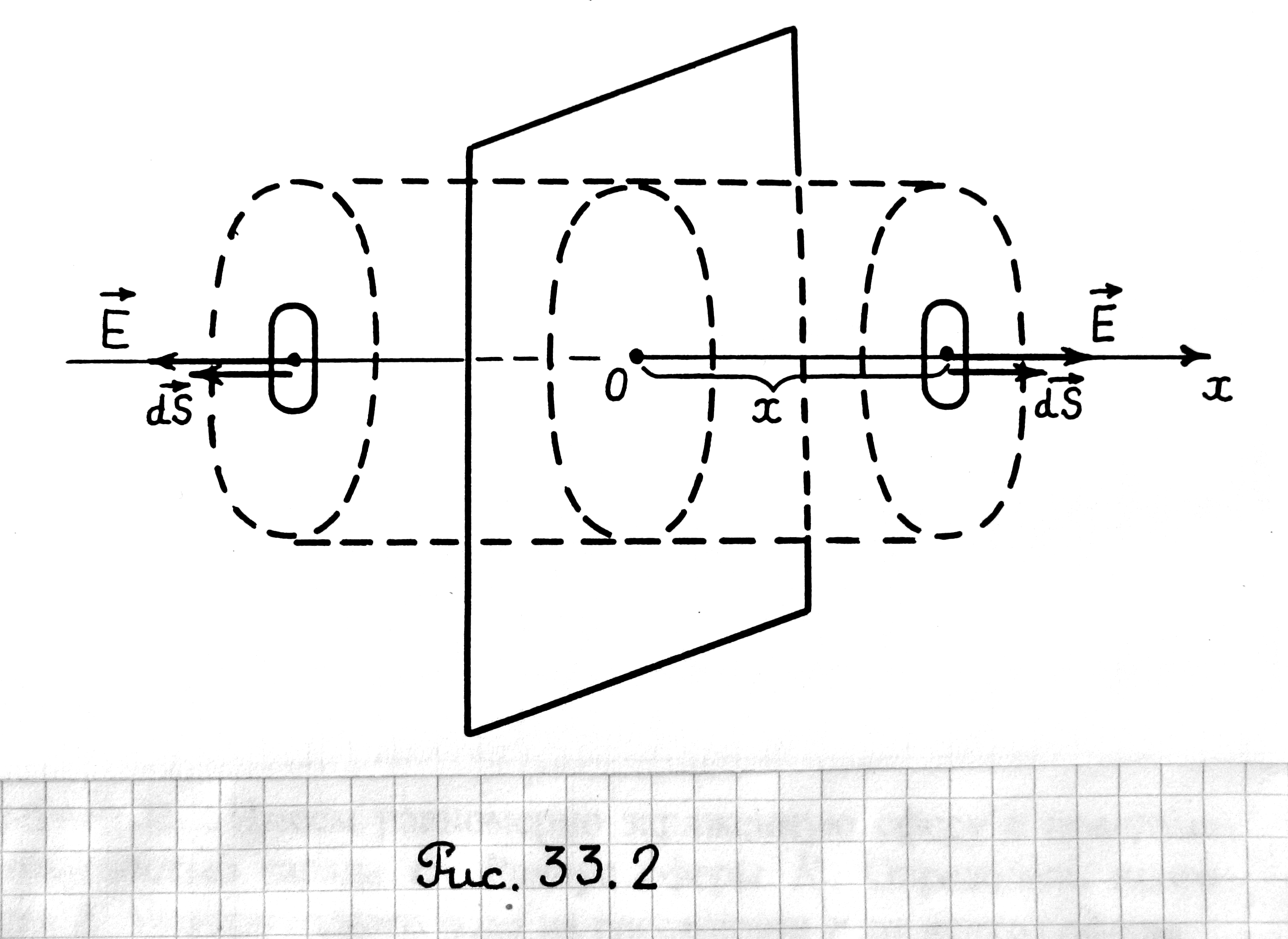
Рис. 33.2

Согласно теореме Гаусса

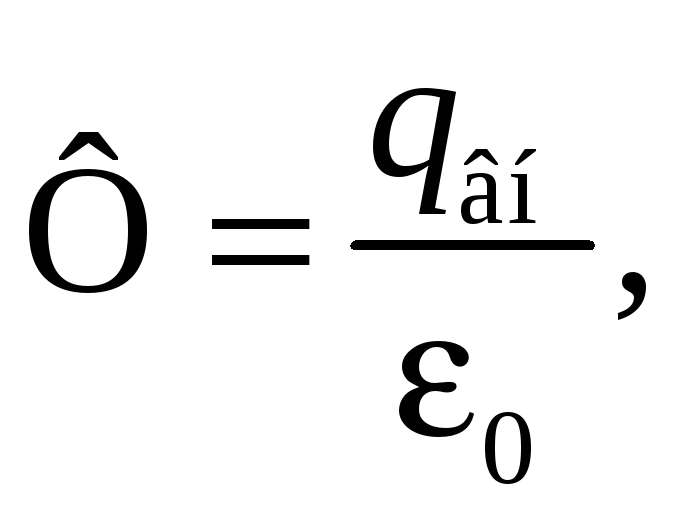(33.3)

где — заряд плоскости, сосредоточенный внутри цилиндра. Найдем его. По определению, поверхностная плотность заряда

В случае равномерно заряженной плоскости (σ = const) можем написать

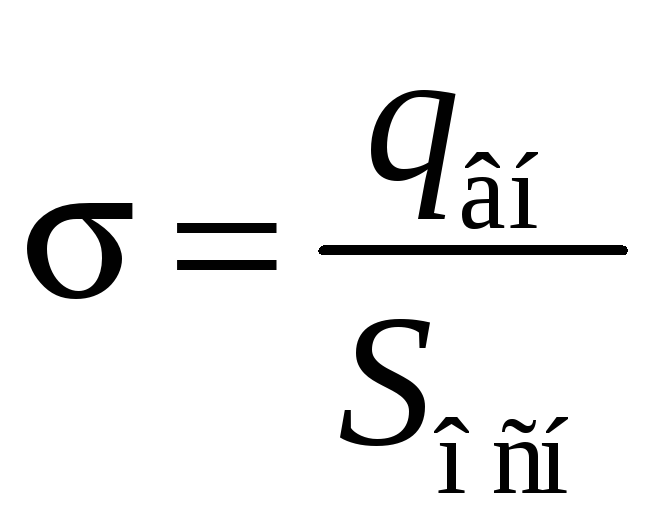
(из рис. 33.2 видно, что заряд сосредоточен на части плоскости с площадью S_осн), откуда

(33.4)

Подставляя выражения (33.2) и (33.4) в соотношение (33.3), получаем

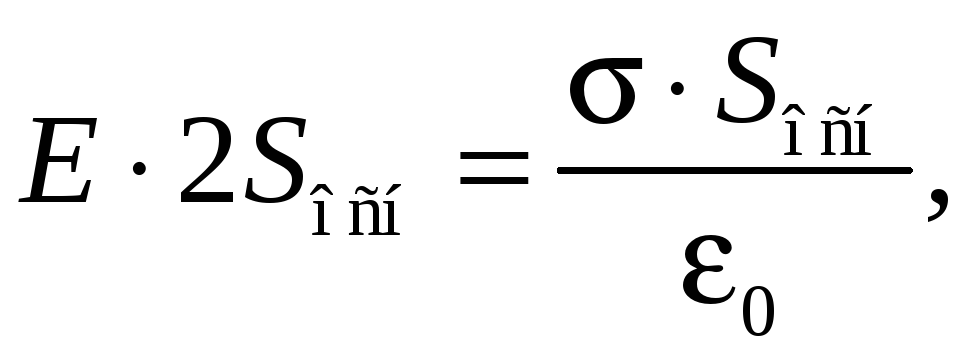
откуда

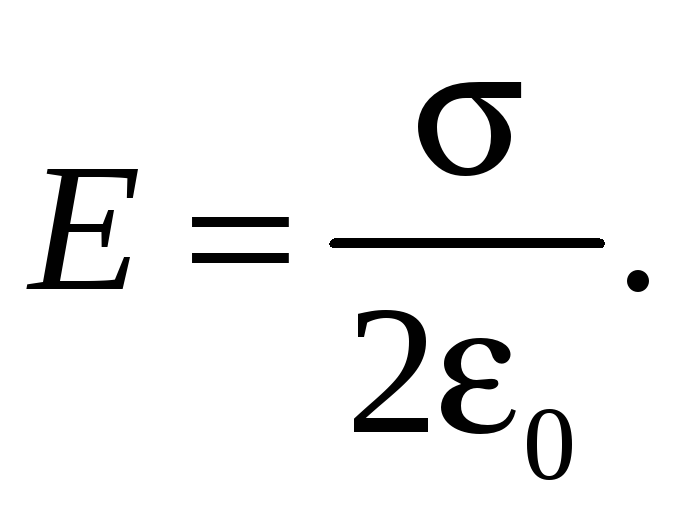(33.5)

Из выражения (33.5) видно, что E не зависит от расстояния x от заряженной плоскости, т. е.

Следовательно, электрическое поле, создаваемое бесконечной равномерно заряженной плоскостью, является однородным.

Пример 33.2. Имеем равномерно заряженную сферу с поверхностной плотностью заряда σ. Радиус сферы R. Определить напряженность Е электрического поля на расстоянии r от центра сферы.

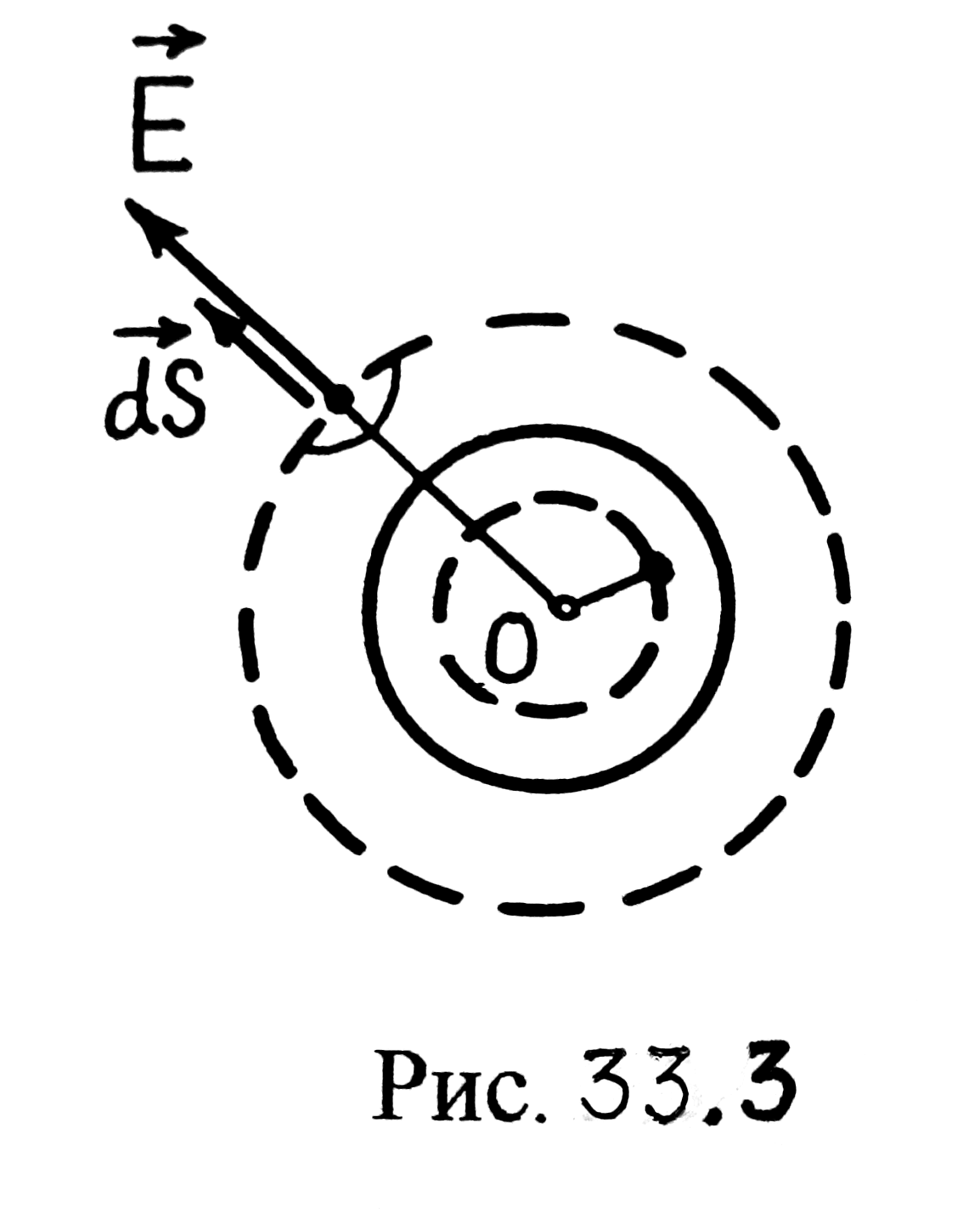
Дано: σ R r	Решение Сначала определим Е в точке, находящейся внутри заряженной сферы (r < R). Проведем через нее гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.3). Согласно теореме Гаусса
E – ?

(из рис. 33.3 видно, что заряда внутри гауссовой поверхности нет), откуда следует, что

Следовательно, внутри заряженной сферы напряженность Е электрического поля равна нулю.

Теперь определим Е в точке, находящейся вне заряженной сферы (r > R). Пусть сфера заряжена положительно. Вследствие симметрии вектор Е поля, создаваемого сферой, в интересующей нас точке направлен радиально от центра сферы.

Рис. 33.3

Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.3). Найдем поток вектора сквозь гауссову поверхность:

(33.6)

При интегрировании мы учли, что для всех точек гауссовой сферы α = 0 и Е = = const.

Согласно теореме Гаусса

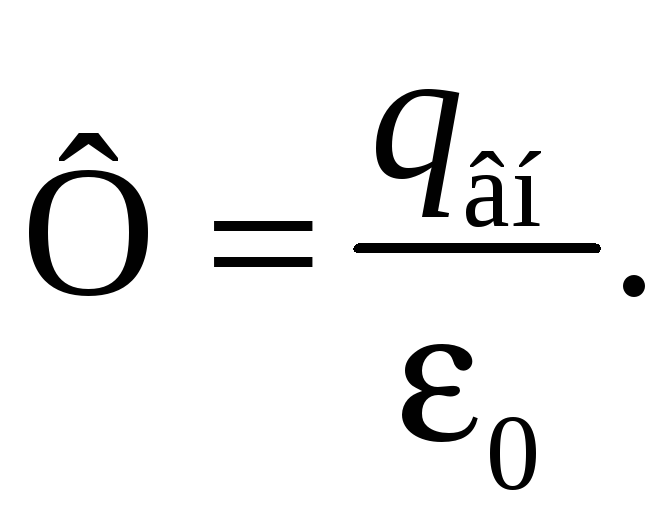(33.7)

Из рис. 33.3 видно, что заряженная сфера находится внутри гауссовой поверхности и поэтому заряд q_вн равен заряду q_сф сферы. В случае равномерно заряженной сферы (σ = const) можем записать

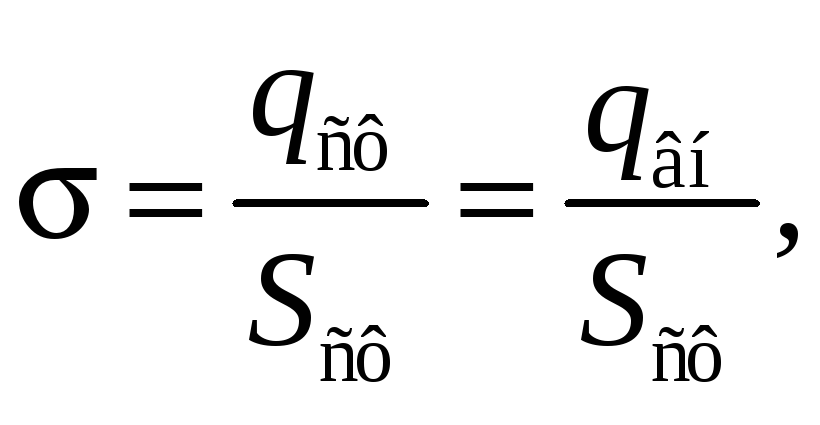
откуда

(33.8)

Подставляя выражения (33.6) и (33.8) в соотношение (33.7), получаем

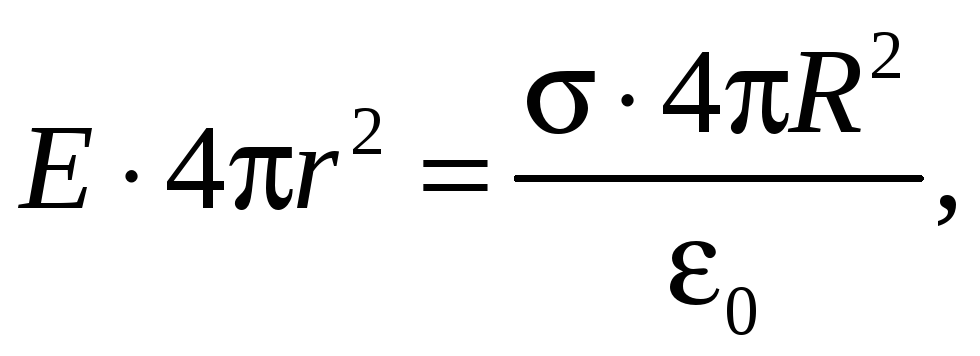
откуда

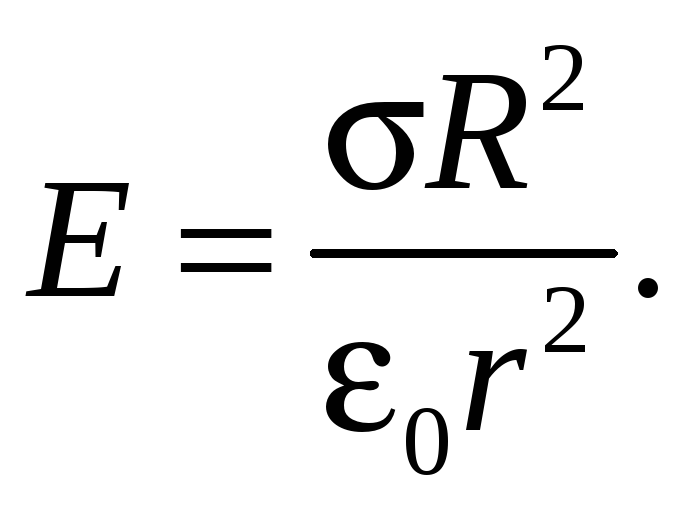(33.9)

Следовательно, напряженность Е поля вне заряженной сферы убывает с расстоянием r. Графически зависимость E(r) электрического поля равномерно заряженной сферы представлена на рис. 33.4.

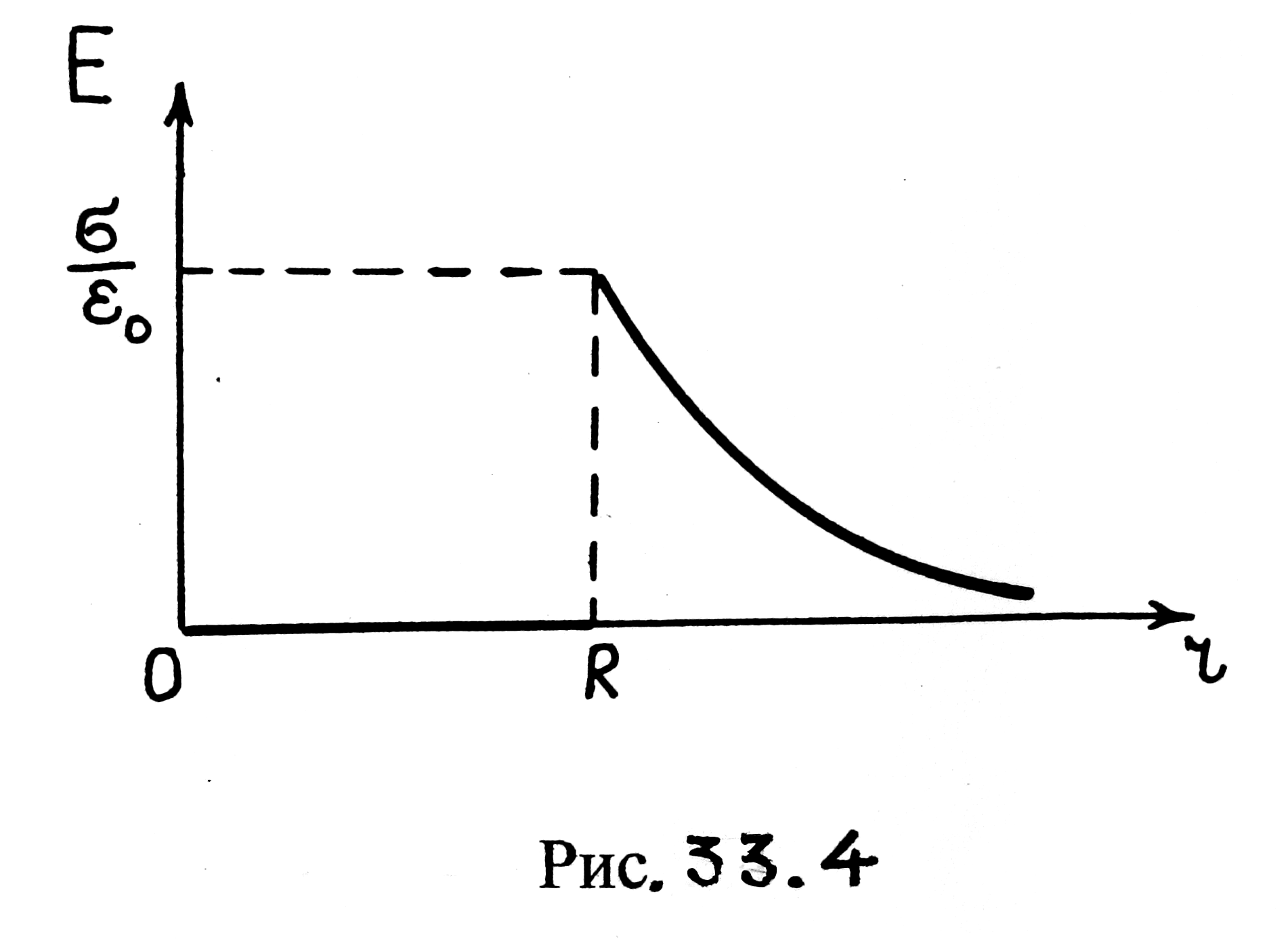
Рис. 33.4

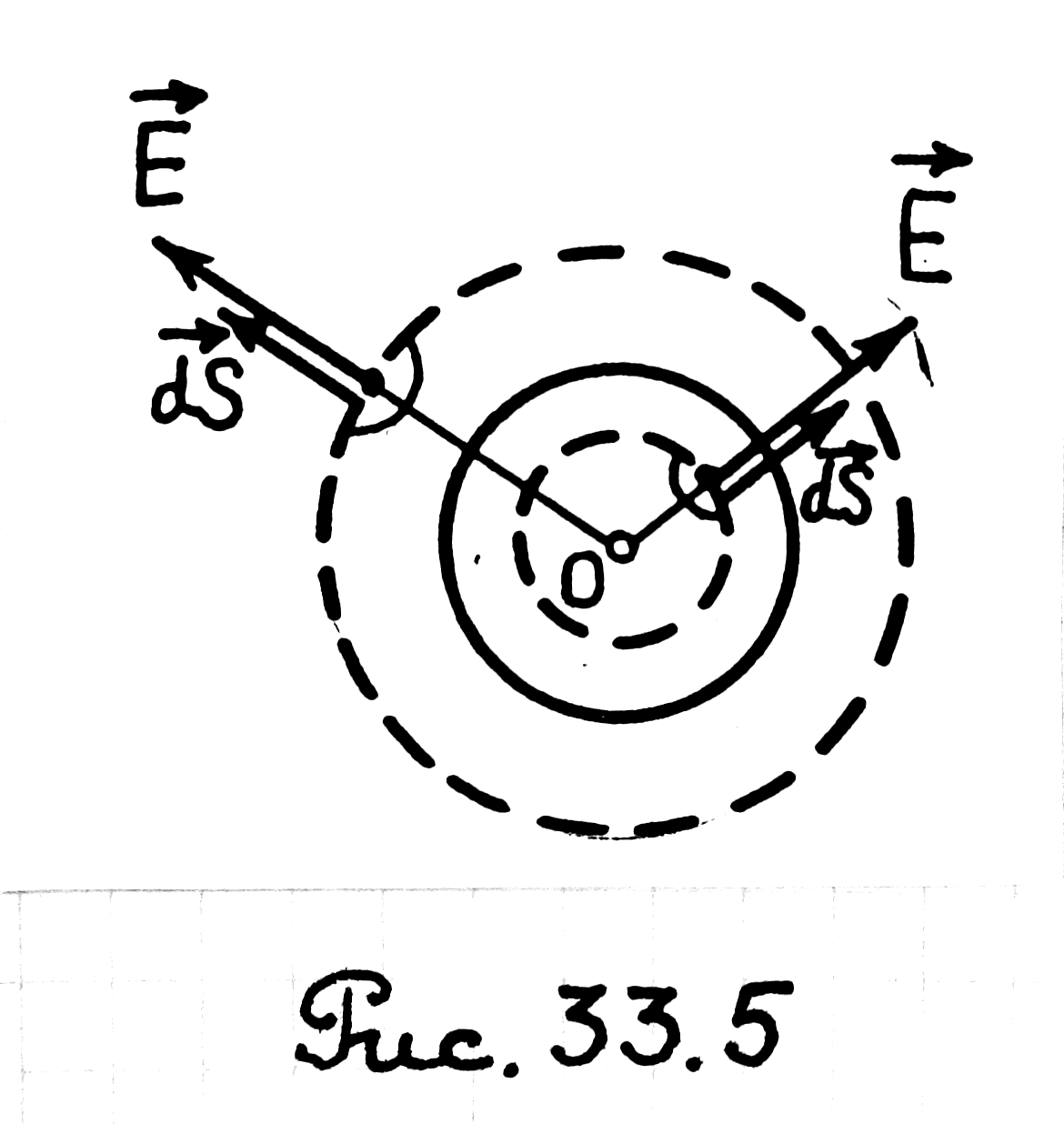
Пример 33.3. Имеем равномерно заряженный шар с объемной плотностью заряда ρ. Радиус шара R. Определить напряженность Е электрического поля на расстоянии r от центра шара.

Дано: ρ R r	Решение Сначала определим Е в точке, находящейся внутри заряженного шара (r < R). Пусть шар заряжен положительно. Вследствие симметрии вектор поля, создаваемого шаром, в интересующей нас точке направлен радиально от центра шара.
E – ?

Рис. 33.5

Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.5). Найдем поток вектора сквозь гауссову поверхность:

(33.10)

При интегрировании мы учли, что для всех точек гауссовой сферы α = 0 и Е = const.

Согласно теореме Гаусса

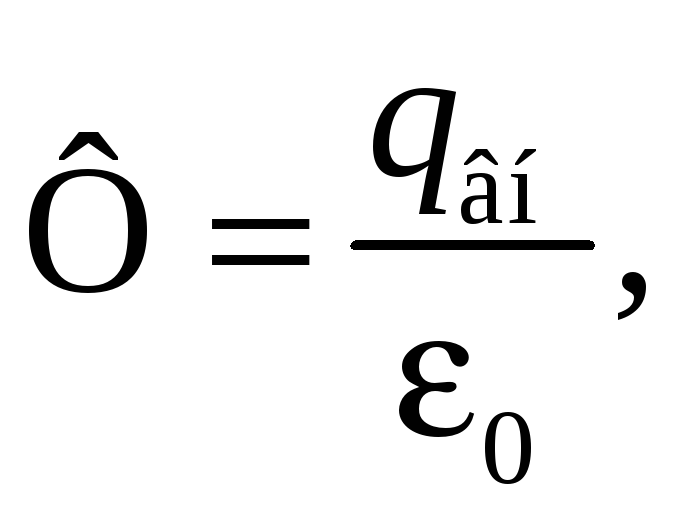(33.11)

где — заряд части шара, сосредоточенный внутри гауссовой сферы. Найдем его. По определению, объемная плотность заряда

В случае равномерно заряженного шара (ρ = const) можем написать

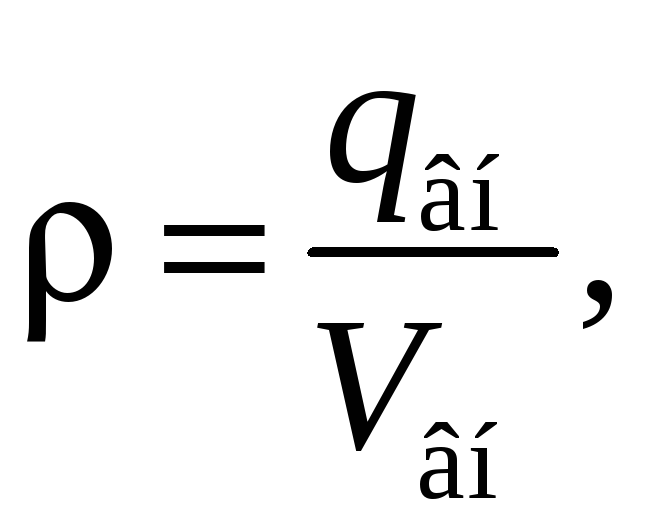(33.12)

где — объем шара внутри гауссовой сферы. Из выражения (33.12) находим

(33.13)

Подставляя выражения (33.10) и (33.13) в соотношение (33.11), получаем

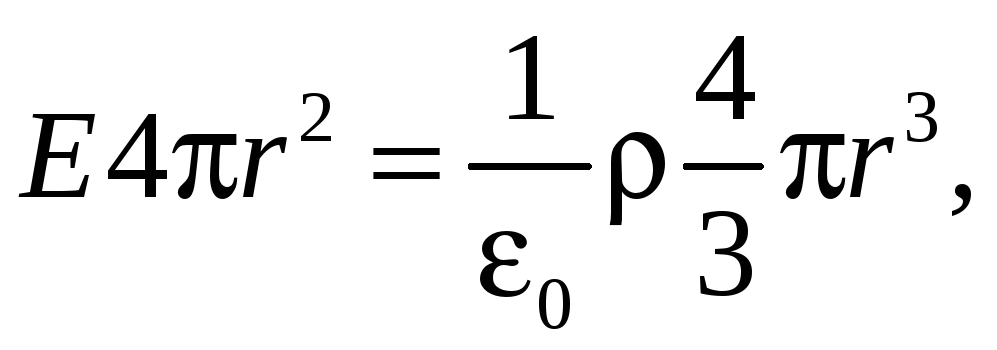
откуда

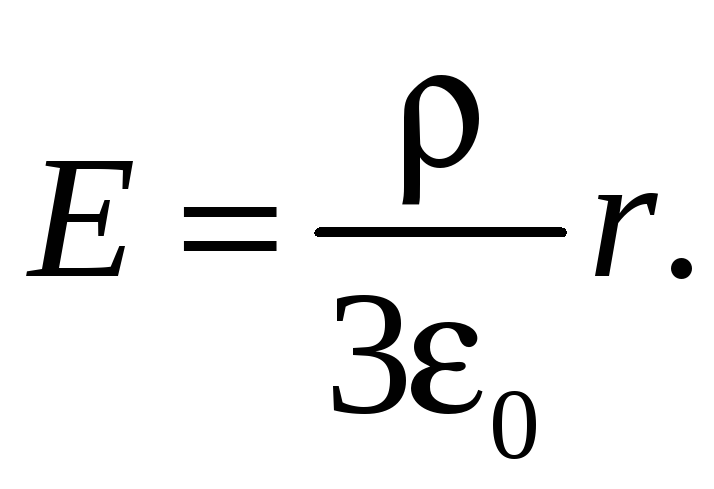(33.14)

Следовательно, напряженность Е поля вне заряженной сферы возрастает с расстоянием r.

Теперь, рассуждая аналогично, определим Е в точке, находящейся вне заряженного шара (r > R). Из рис. 33.5 видно, что весь заряженный шар находится внутри гауссовой поверхности и поэтому q_вн равен заряду q_ш шара. Можем написать

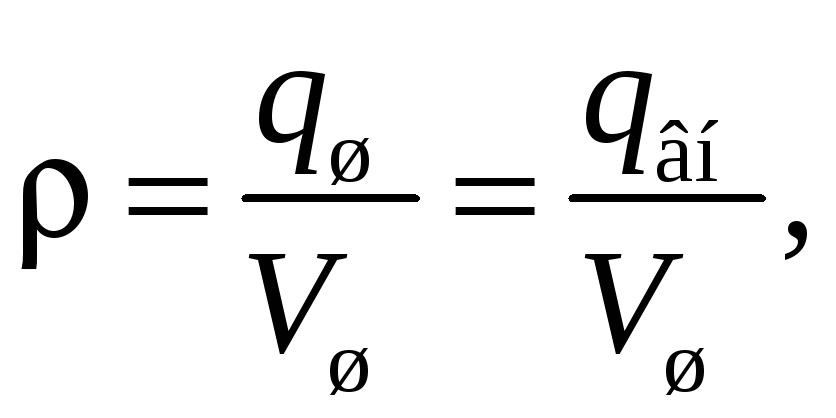
откуда

Из соотношения

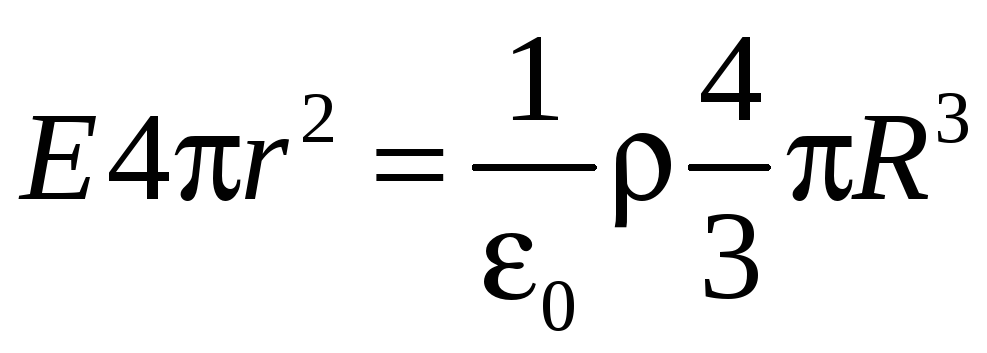
следует

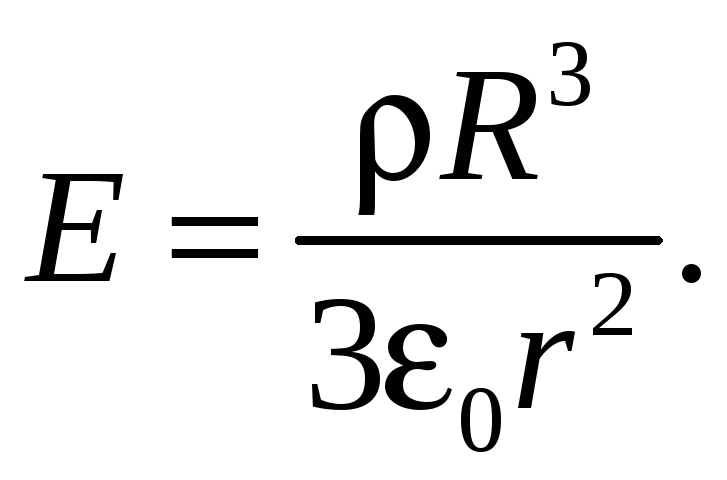(33.15)

Следовательно, напряженность Е поля вне заряженного шара убывает с расстоянием r. Графически зависимость E(r) электрического поля равномерно заряженного шара представлена на рис. 33.6.

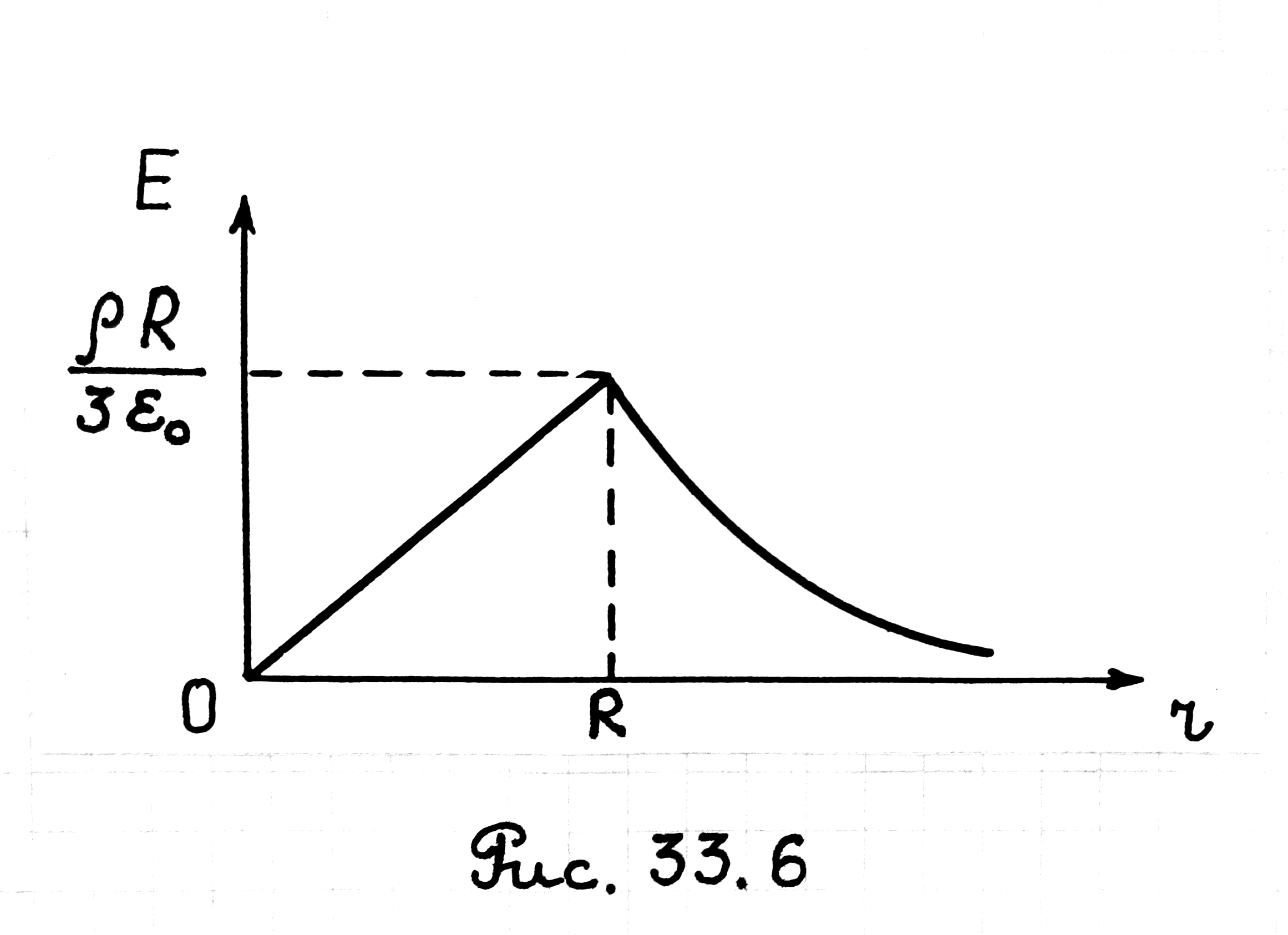
Рис. 33.6