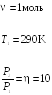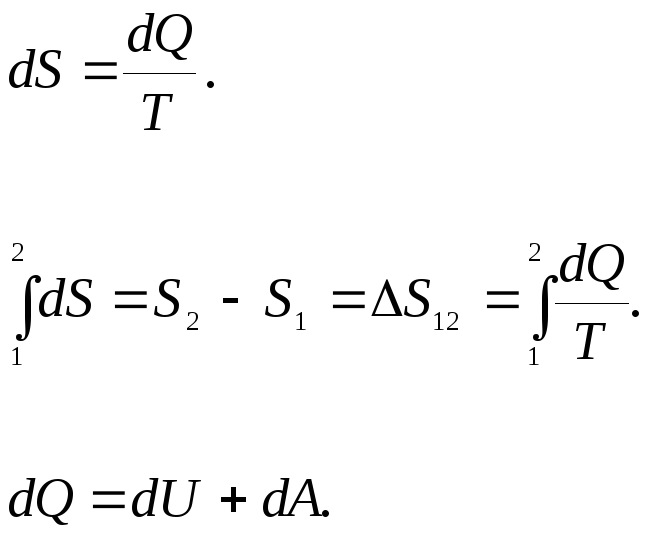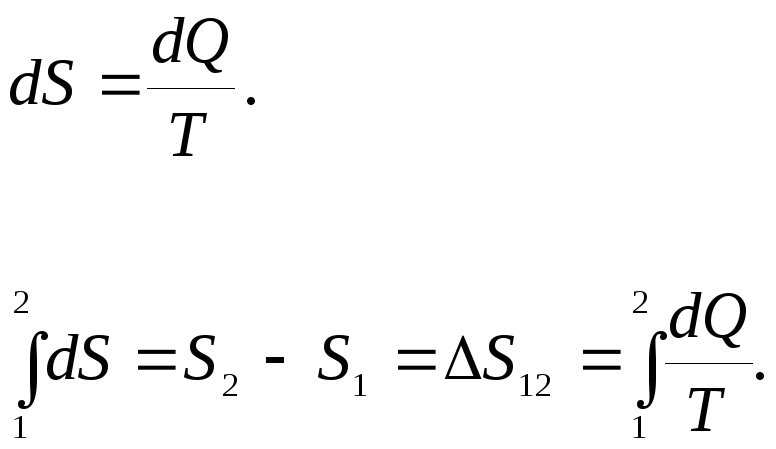- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
§ 24. Адиабатический процесс
Адиабатическим
называют
процесс, в котором система не обменивается
теплотой с внешней средой
![]() .
.
Найдем
связь между давлением
![]() и объемом
и объемом
![]() идеального газа в адиабатическом
процессе.
идеального газа в адиабатическом
процессе.
Дифференцируя уравнение Клапейрона – Менделеева
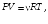
получаем
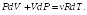
(24.1)
Из
первого закона термодинамики (22.3) при
![]() следует с учетом выражений (22.6), (23.6) и
(23.8)
следует с учетом выражений (22.6), (23.6) и
(23.8)
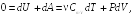
откуда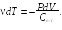
(24.2)
Подставляя выражение (24.2) в соотношение (24.1), имеем
![]()
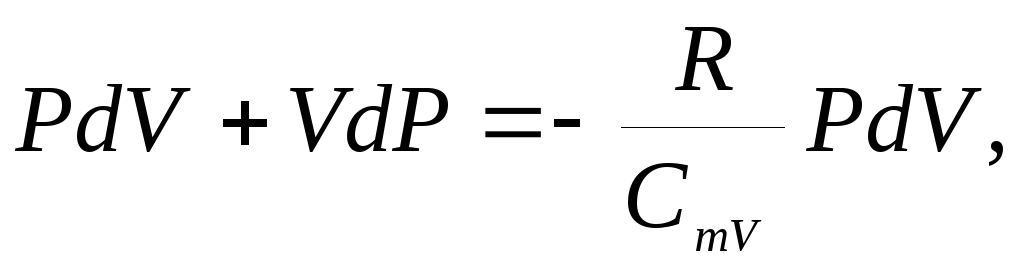
откуда с учетом уравнения Майера (23.14)
![]()
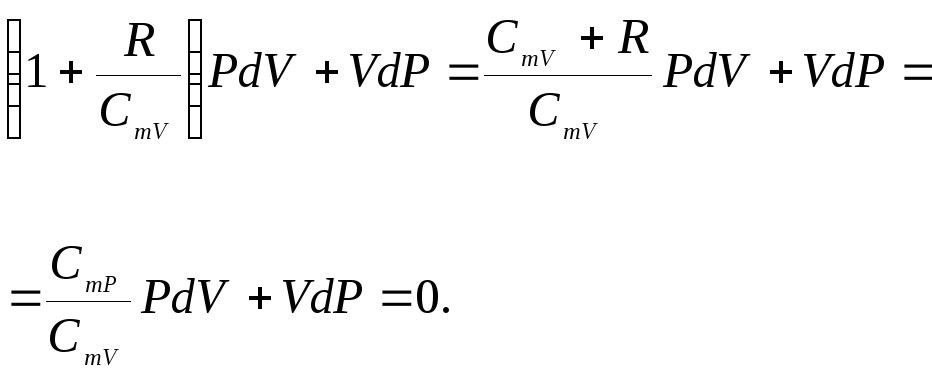 (24.3)
(24.3)
Разделим
уравнение (24.3) на
![]() и проинтегрируем:
и проинтегрируем:
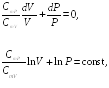
откуда
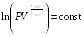
или
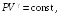
(24.4)
где
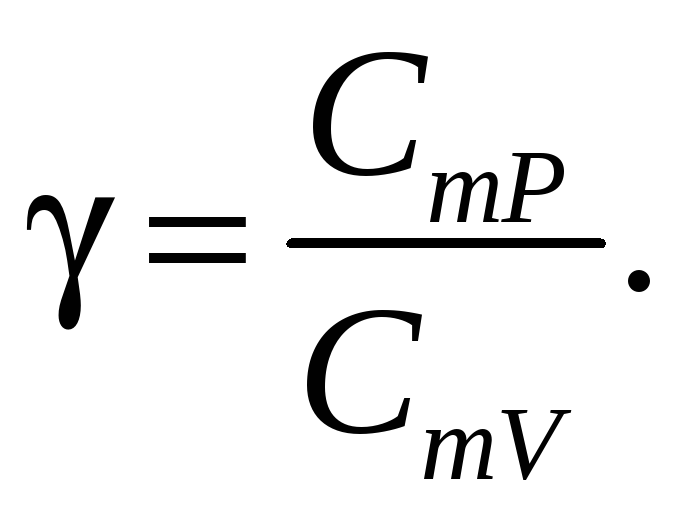
Уравнение (24.4) называют уравнением Пуассона, а безразмерную величину γ — коэффициентом Пуассона или показателем адиабаты. С учетом выражений (23.8) и (23.15)
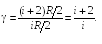
(24.5)
Кривую, изображающую адиабатический процесс, называют адиабатой (рис. 24.1).
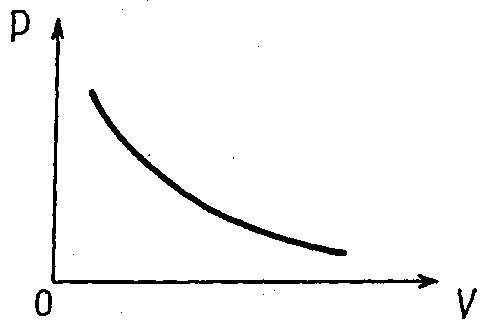
Рис. 24.1
Практически адиабатический процесс осуществляется при быстром расширении или сжатии газа.
Пример
24.1. Один моль
кислорода, находившегося при температуре
![]() адиабатически сжали так, что его давление
возросло в
адиабатически сжали так, что его давление
возросло в
![]() раз. Найти работу
раз. Найти работу
![]() ,
которая была совершена над газом.
,
которая была совершена над газом.
|
Дано:
|
Решение
|
|
|
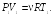
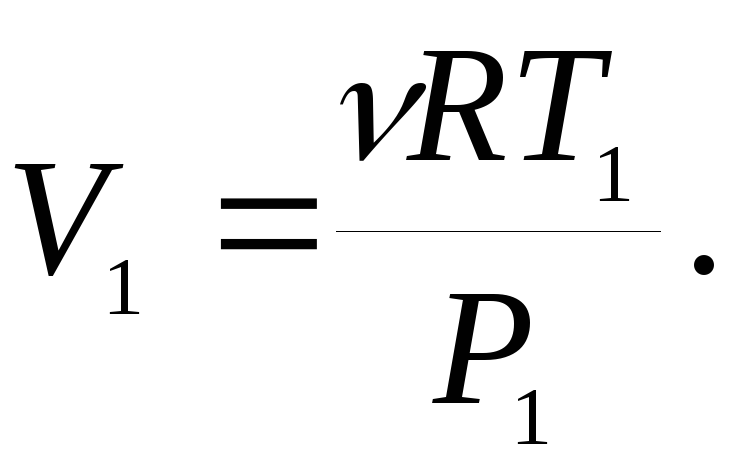
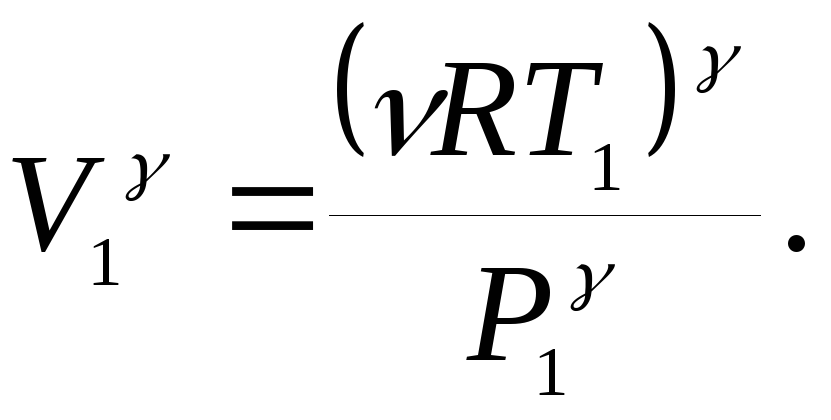
![]()
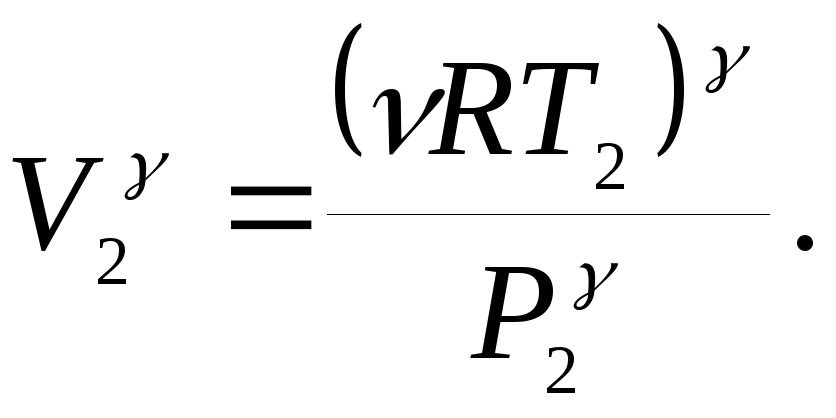
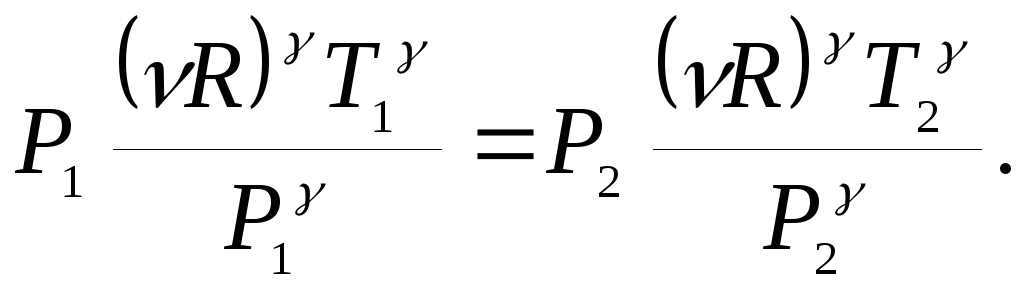
![]()
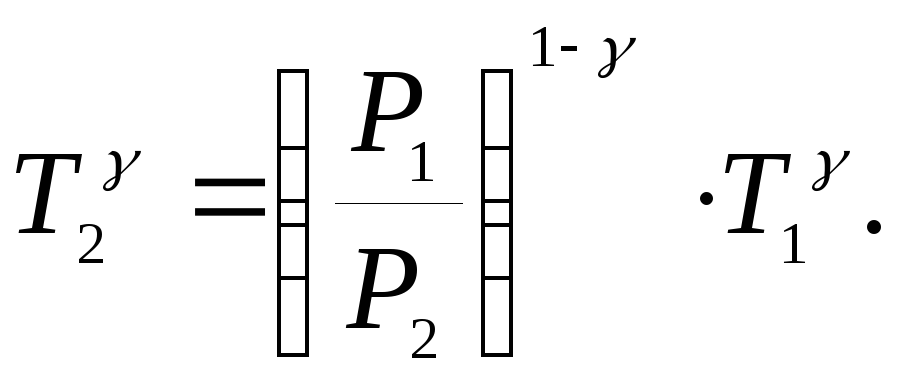
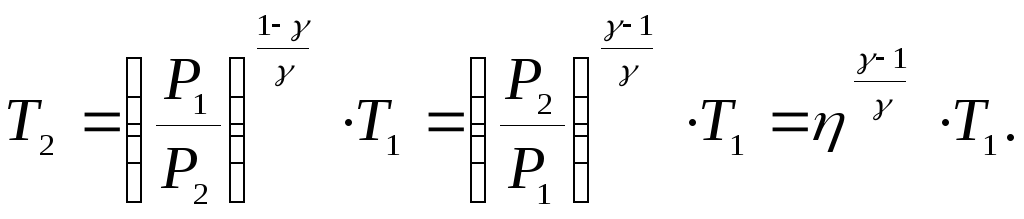
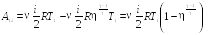
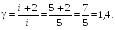
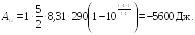
Ответ:
![]()
§ 25. Энтропия
Набором
макроскопичесих параметров, например,
![]() и
и
![]() ,
задается состояние системы в целом или
макросостояние
системы.
Набор параметров
,
задается состояние системы в целом или
макросостояние
системы.
Набор параметров
![]() и
и
![]() выражает осредненное суммарное состояние
большого числа молекул, из которых
состоит система. Назовем микросостоянием
системы
состояние всех молекул, образующих
систему. Состояние каждой молекулы
определяется заданием ее координат и
скорости в данный момент времени.
Очевидно, что микросостояние системы
непрерывно меняется. Однако набор
макроскопических параметров
выражает осредненное суммарное состояние
большого числа молекул, из которых
состоит система. Назовем микросостоянием
системы
состояние всех молекул, образующих
систему. Состояние каждой молекулы
определяется заданием ее координат и
скорости в данный момент времени.
Очевидно, что микросостояние системы
непрерывно меняется. Однако набор
макроскопических параметров
![]() и
и
![]() ,
а следовательно, и макросостояние
системы при этом может не меняться.
Назовем термодинамической
вероятностью
,
а следовательно, и макросостояние
системы при этом может не меняться.
Назовем термодинамической
вероятностью
![]() число
различных микросостояний, соответствующих
данному макросостоянию.
число
различных микросостояний, соответствующих
данному макросостоянию.
Вероятность
макросостояния пропорциональна его
термодинамической вероятности. Для
равновесного состояния системы, при
котором параметры
![]() ,
,
![]() ,
и
,
и
![]() остаются неизменными,
остаются неизменными,
![]() имеет максимальное значение по сравнению
с любым неравновесным состоянием.
Поэтому равновесное состояние наиболее
вероятно. Если система переходит из
неравновесного состояния в равновесное,
то такой процесс необратим.
имеет максимальное значение по сравнению
с любым неравновесным состоянием.
Поэтому равновесное состояние наиболее
вероятно. Если система переходит из
неравновесного состояния в равновесное,
то такой процесс необратим.
Определить
вероятность состояния через
термодинамическую вероятность неудобно,
так как
![]() не обладает свойством аддитивности
(нельзя складывать). Действительно, если
мысленно разбить термодинамическую
систему на
не обладает свойством аддитивности
(нельзя складывать). Действительно, если
мысленно разбить термодинамическую
систему на
![]() подсистем с термодинамическими
вероятностями
подсистем с термодинамическими
вероятностями
![]() (рис 25.1),
(рис 25.1),
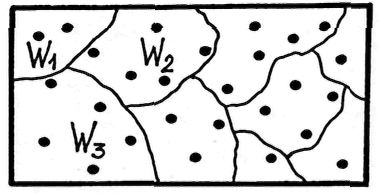
Рис. 25.1
то термодинамическая вероятность системы
![]() (25.1)
(25.1)
откуда
видно, что
![]() не является аддитивной величиной.
не является аддитивной величиной.
Взяв логарифм от соотношения (25.1), получим
![]()
откуда
видно, что
![]() — аддитивная величина (можно складывать).
— аддитивная величина (можно складывать).
Введем физическую величину
(![]() 25.2)
25.2)
где
![]() — постоянная Больцмана. Величину
— постоянная Больцмана. Величину
![]() называют энтропией
системы. Она
характеризует вероятность макросостояния
системы. Определение энтропии (25.2) было
сделано Больцманом.
называют энтропией
системы. Она
характеризует вероятность макросостояния
системы. Определение энтропии (25.2) было
сделано Больцманом.
Дадим еще одно определение энтропии. Рассмотрим расширение газа в пустоту (рис. 25.2).

Рис. 25.2
Расчет дает
![]()
где
![]() — число молекул газа в объеме
— число молекул газа в объеме
![]() ,
или
,
или
![]() ,
,
где
![]() — коэффициент пропорциональности.
— коэффициент пропорциональности.
Очевидно,
в нашем случае
![]() ,
так как
,
так как
![]() .
С учетом выражения (25.2) можем написать
.
С учетом выражения (25.2) можем написать
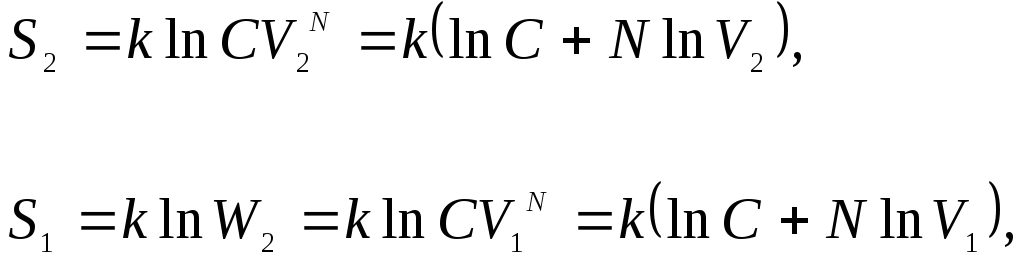
откуда приращение энтропии
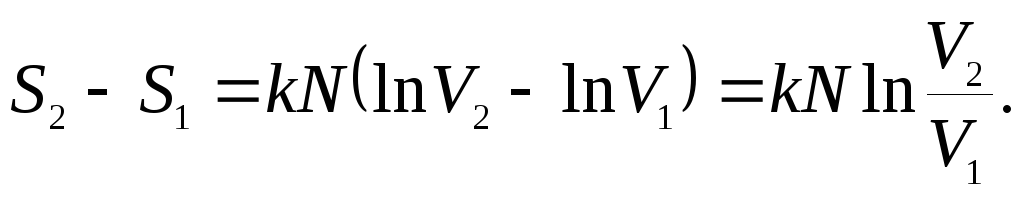
(25.3)
Учитывая,
что
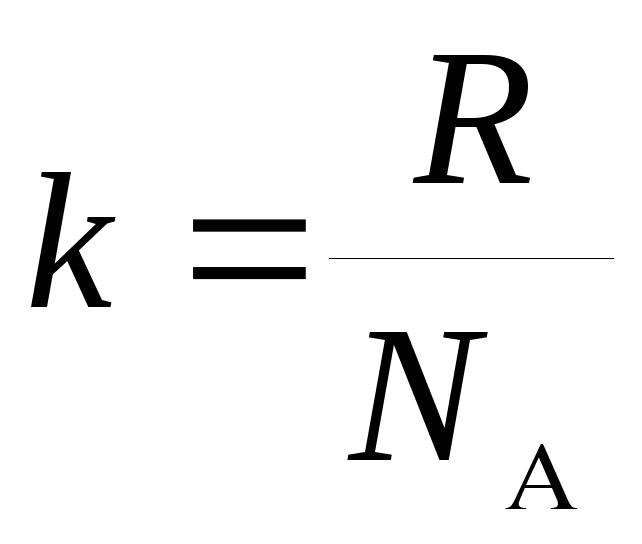 и
и
![]() ,
перепишем выражение (25.3) в виде
,
перепишем выражение (25.3) в виде
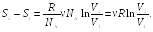
(25.4)
При
изотермическом увеличении объема газа
от
![]() до
до
![]() при температуре
при температуре
![]() количество тепла, полученное газом,
количество тепла, полученное газом,
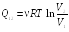
(25.5)
(см. пример 23.1). Сравнивая выражение (25.4) и (25.5), получаем
![]()
(25.6)
или для элементарного приращения энтропии
![]()
(25.7)
Формула (25.7) верна не только для изотермического процесса, но и для любого равновесного обратимого процесса
![]()
(25.8)
Определение энтропии (25.7) было сделано Клаузиусом.
Из выражений (25.2) и (25.6) следует, что энтропия является функцией состояния системы.
Пример
25.1. Определить
приращение энтропии
![]() при изотермическом кислороде массой M
= 10 г от объема
V1
= 25 л до объема V2
= 100 л.
при изотермическом кислороде массой M
= 10 г от объема
V1
= 25 л до объема V2
= 100 л.
|
Дано:
M = 10 г
V1 = 25 л
V2 = 100 л |
Решение
|
|
|
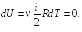
![]()
![]()
![]()
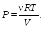
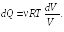
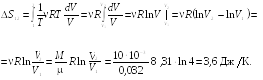
Ответ:
![]()
Пример
25.2. Пять
молей гелия изохорически переводят из
состояния, в котором его давление
![]() в состояние, в котором его давление
в состояние, в котором его давление
![]() Определить приращение энтропии
Определить приращение энтропии
![]() гелия.
гелия.
|
Дано:
|
Решение
|
|
|
![]()
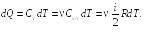
.
2
1
2
1
T
T
i
T
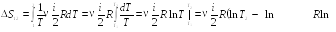
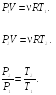
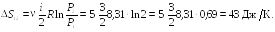
Ответ:
![]()