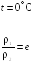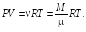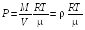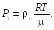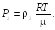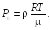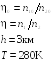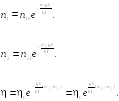- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
§ 18. Барометрическая формула
До
сих пор мы считали, что молекулы газа
равномерно распределены по объему
сосуда. Однако это не так. На молекулы
газа действуют силы гравитационного
притяжения Земли. Если бы не было
теплового движения молекул атмосферного
воздуха, то все они упали бы на землю. С
другой стороны, если бы не было сил
притяжения Земли, то атмосферный воздух
рассеялся бы по всей Вселенной. Совместные
действия гравитационного поля Земли и
теплового движения молекул приводят к
такому состоянию атмосферы, при котором
число молекул
![]() в единице объема и давление
в единице объема и давление
![]() воздуха убывают с возрастанием высоты
воздуха убывают с возрастанием высоты
![]() над земной поверхностью.
над земной поверхностью.
Найдем
закон изменения давления газа с высотой
в однородном гравитационном поле
(ускорение свободного падения
![]() ).
Будем считать, что газ находится в
равновесном состоянии при температуре
).
Будем считать, что газ находится в
равновесном состоянии при температуре
![]() .
.
Согласно
закону гидростатики, запишем выражение
для давления газа на высотах
![]() и
и
![]() :
:
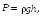
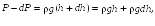
откуда
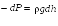
или
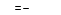
(18.1)
где — плотность газа.
Из уравнения Клапейрона – Менделеева
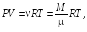
где
![]() — масса газа в объемe
V;
μ — масса моля газа, следует
— масса газа в объемe
V;
μ — масса моля газа, следует
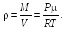
(18.2)
Подставляя выражение (18.2) в соотношение (18.1), получаем
![]()
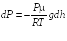
или
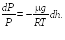
(18.3)
Проинтегрируем выражение (18.3):
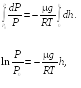
откуда
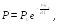
(18.4)
где
![]() — давление газа;
— давление газа;
![]()
Представим зависимость (18.4) графически для двух газов с разными μ (рис. 18.1).
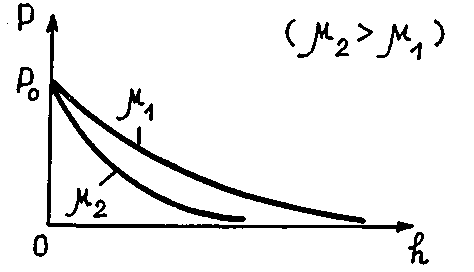
Рис. 18.1
Из рис. 18.1 видно, что давление газа убывает с высотой быстрее, чем тяжелее газ (чем больше μ). Следовательно, в верхних слоях атмосферы должны преобладать легкие газы.
Выражение
(18.4) можно применять и для атмосферного
воздуха, считая его газовой смесью с
![]() Измеряя давление
Измеряя давление
![]() и
и
![]() воздуха с помощью барометра, можно
определить высоту
воздуха с помощью барометра, можно
определить высоту
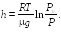
Поэтому выражение (18.4) называют барометрической формулой. Барометр, специально проградуированный для отсчета высоты над уровнем моря, называют альтиметром. Он широко применяется в авиации, альпинизме и т. д.
Пример
18.1. Считая,
что температура и молярная масса воздуха,
а также ускорение свободного падения
не зависят от высоты, найти разность
высот, на которых плотности воздуха при
температуре 0 °С отличаются в
![]() раз.
раз.
|
Дано:
|
Решение
.
|
|
|
![]() .
.
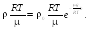
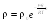 .
.
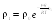 .
.
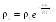 .
.
.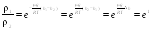
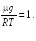
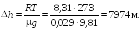
Ответ:
![]()
§ 19. Распределение Больцмана
Барометрическая
формула (18.4) позволяет найти зависимость
числа молекул
![]() в единице объема газа от высоты
в единице объема газа от высоты
![]() над земной поверхностью. По-прежнему
будем считать, что газ находится в
равновесном состоянии при температуре
над земной поверхностью. По-прежнему
будем считать, что газ находится в
равновесном состоянии при температуре
![]() в
однородном гравитационном поле (
в
однородном гравитационном поле (![]() ).
).
Из уравнения Клапейрона – Менделеева следует
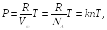
(19.1)
где
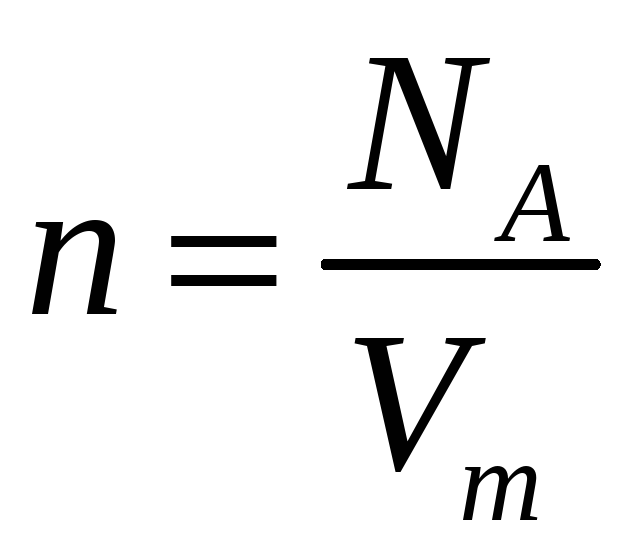 — число молекул газа в единице объема.
— число молекул газа в единице объема.
Подставим выражение (19.1) в барометрическую формулу, имеем
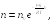
(19.2)
где
![]() — число молекул в единице объема газа
при
— число молекул в единице объема газа
при
![]() .
.
Можем написать
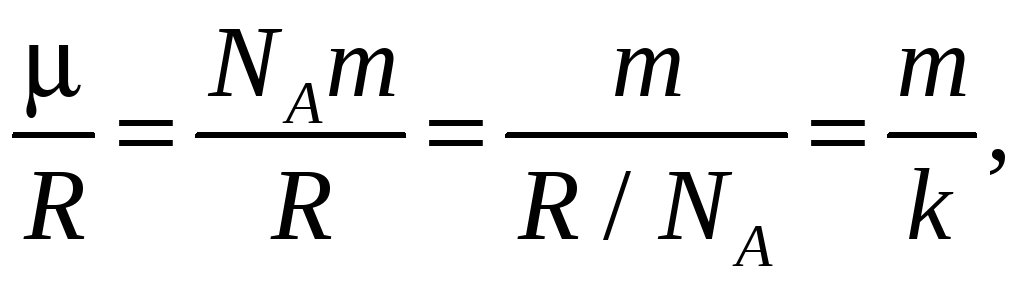 (19.3)
(19.3)
где
![]() — масса молекулы;
— масса молекулы;
![]() — постоянная Больцмана.
— постоянная Больцмана.
Подставляем формулу (19.3) в соотношение (19.2), получаем
![]()
(19.4)
или
![]()
![]() (19.5)
(19.5)
где
![]() — потенциальная энергия молекулы газа
в гравитационном поле Земли.
— потенциальная энергия молекулы газа
в гравитационном поле Земли.
Следовательно,
найденная зависимость (19.4)
![]() от
от
![]() переходит в зависимость (19.5)
переходит в зависимость (19.5)
![]() от
от
![]() (рис. 19.1),
согласно которой в объеме газа молекул
будет больше там, где их потенциальная
энергия меньше.
(рис. 19.1),
согласно которой в объеме газа молекул
будет больше там, где их потенциальная
энергия меньше.
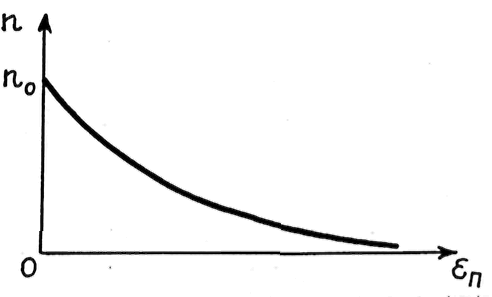
Рис. 19.1
Больцман доказал, что распределение (19.5) справедливо не только для молекул газа в потенциальном гравитационном поле Земли, но и для совокупности любых одинаковых хаотически движущихся частиц в любом потенциальном силовом поле. Поэтому распределение (19.5) называют распределение Больцмана.
Пример 19.1. Пусть η0 — отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а η — соответствующее отношение на высоте h = 3 км. Найти отношение η/η0 при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты.
|
Дано:
|
Решение
|
|
η/η0 – ?
|
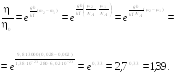
Ответ: η/η0 = 1,39.