§ 16. Внутренняя энергия идеального газа

Внутреннюю энергию газа определяют как сумму кинетической энергии теплового движения молекул и потенциальной энергии межмолекулярного взаимодействия.

Получим выражение для внутренней энергии идеального газа. В идеальном газе пренебрегают силами межмолекулярного взаимодействия. Поэтому внутренняя энергия идеального газа равна кинетической энергии его молекул.

Расчет дает, что средняя кинетическая энергия молекул

(16.1)

где — температура газа; — постоянная Больцмана

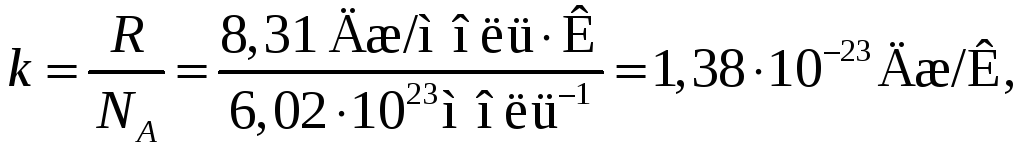( где N_A — число Авогадро — число молекул в одном моле газа); — число степеней свободы — число независимых координат, с помощью которых может быть задано положение молекул в пространстве. Для определения положения в пространстве одноатомной молекулы достаточно трех координат . Следовательно, для одноатомной молекулы . Для определения положения в пространстве двухатомной молекулы достаточно трех координат центра молекулы и двух значений углов φ и υ, фиксирующих направление оси молекулы. Следовательно, для двухатомной молекулы . Для определения положения трехатомной и более молекулы в пространстве достаточно трех координат центра молекулы и трех значений углов φ, υ и ψ, фиксирующих направление оси молекулы. Следовательно, для трехатомной и многоатомной молекулы .

Пусть в сосуде находится N молекул идеального газа. Тогда с учетом выражения (16.1) внутренняя энергия идеального газа

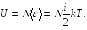
(16.2)

Учитывая, что

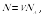
можем написать

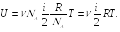
(16.3)

Отметим, что внутренняя энергия является функцией состояния. Это означает, например, что при переходе газа из состояния 1 (с температурой ) в состояние 2 (с температурой ) приращение внутренней энергии , т. е. не зависит от способа перехода газа из состояния 1 в состояния 2, а определяется только разностью значений внутренней энергии газа в состояния 1 и 2.

Пример 16.1. Водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л, охладили на . Найти приращение внутренней энергии газа.

Дано: V = 5 л	Решение > . .

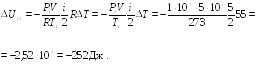
Ответ:

Пример 16.2. Водород занимает объем при давлении Его нагрели при постоянном объеме до давления Определить приращение внутренней энергии газа.

Дано:	Решение

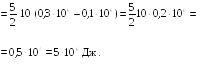
Ответ:

§ 17. Распределение Максвелла

Назовем состояние газа равновесным, если параметры состояния газа при отсутствии внешних воздействий остаются неизменными во времени.

Пусть газ находится в равновесном состоянии при температуре . Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в тот или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например от 10 до 20 м/с или от 20 до 30 м/с, будет приходиться в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется.

Определим вероятность того, что модуль скорости молекулы лежит между v и v + dv. Пусть — общее число молекул в единице объема газа, а — число молекул в единице объема газа, скорости которых лежат между v и v + dv. Тогда искомая вероятность

.

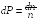
(17.1)

Введем величину

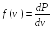
(17.2)

— плотность вероятности, которая является функцией модуля скорости молекулы, в связи с чем ее называют функцией распределения вероятности молекул по скорости или просто функцией распределения молекул по скоростям.

Комбинируя формулы (17.1) и (17.2), получаем

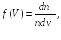
(17.3)

откуда

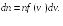(17.4)

Зная вид функции f(v), можно, интегрируя выражение (17.4), определить количество молекул в единице объема газа, скорости которых лежат в любом интервале скоростей.

Максвелл теоретически получил вид функции распределения молекул по скоростям:

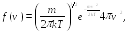
(17.5)

где и — масса молекулы и температура газа; — постоянная Больцмана.

Изобразим график функции (17.5) (рис. 17.1).

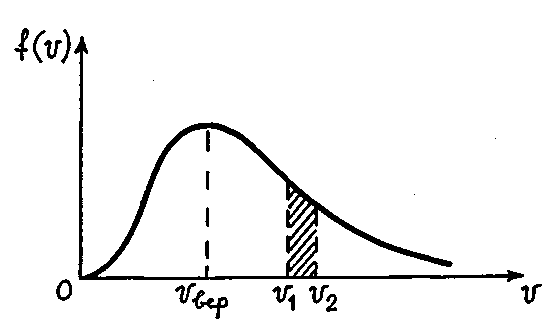
Рис. 17.1

Из графика видно, что вероятность обнаружения в газе молекулы со скоростью, лежащей в интервале от v₁ до v₂ (см. формулу (17.2))

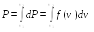
равна заштрихованной площади под кривой f(v).

Вероятность обнаружения в газе молекул с любой скоростью от 0 до

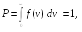
(17.6)

т. е. площадь под всей кривой f(v) равна единице. Выражение (17.6) называют условием нормировки вероятности.

Скорость, соответствующая максимуму функции распределения f(v), будет наиболее вероятной v_вер скоростью молекул. Найдем эту скорость.

Для очевидно

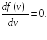
Продифференцируем выражение (17.5) по v и приравняем к нулю.

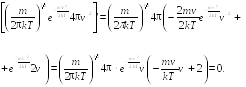
При v = 0 и v = ∞ функция f(v) минимальна. Следовательно, эти значения отбрасываем. Остается

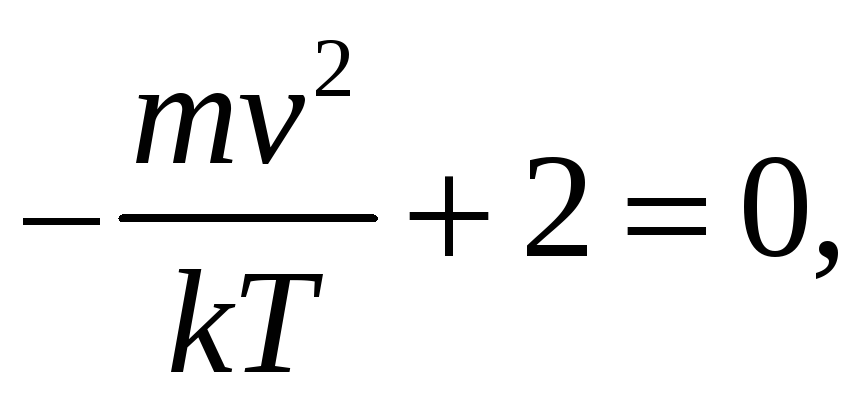
откуда

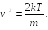
Откуда получаем

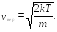
(17.7)

Используя функцию распределения (17.5), можно найти среднюю и среднюю квадратичную v_кв скорости молекул:

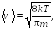
(17.8)

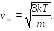(17.9)
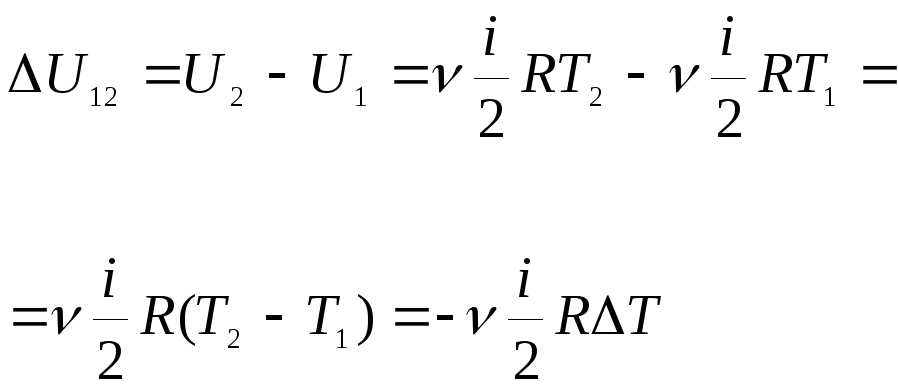
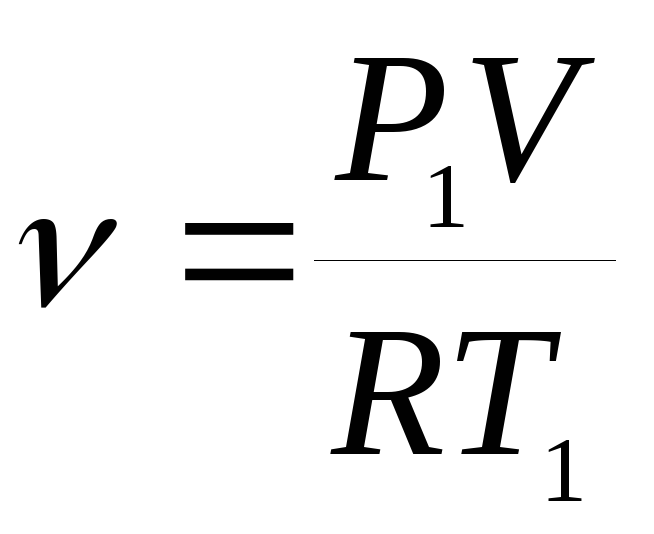