5.4. Основное уравнение динамики для твердого тела, вращающегося вокруг неподвижной оси

Применим уравнение моментов относительно оси к рассмотрению вращательного движения твердого тела.

Рассмотрим твердое тело произвольной формы, вращающееся относительно неподвижной оси (рис.5.6). За ось моментов OZ удобно выбрать ось вращения, направив ее по угловой скорости ().

Уравнение моментов в этом случае имеет вид

Рис.5.6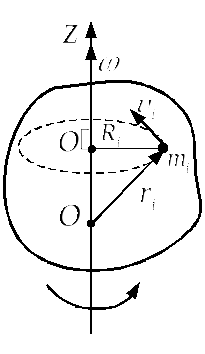

,

где - результирующий момент внешних сил, вызывающий вращение тела, относительно оси OZ.

Найдем связь между моментом импульса тела и угловой скоростью ω. С этой целью мысленно разобьем тело на элементарные массы , которые можно рассматривать как материальные точки.

Момент импульса материальной точки относительно оси OZ равен

,

где и - скорость i-той материальной точки и радиус окружности, которую она описывает при вращении тела.

Учитывая, что , где ω – угловая скорость вращения, одинаковая для всех точек тела, получим

. (5.16)

Момент импульса относительно данной оси всего тела определится суммированием по всем элементарным точкам

. (5.17)

Величина , равная сумме произведений элементарных масс на квадрат их расстояний от некоторой оси, называется моментом инерции тела относительно данной оси:

. (5.18)

Используя (5.18), получим искомую связь между и :

. (5.19)

Таким образом, момент импульса тела относительно оси равен произведению момента инерции тела на его угловую скорость относительно данной оси.

С учетом полученного соотношения (5.19) уравнение моментов принимает вид

или , (5.20)

т.е. произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.

Полученное уравнение представляет собой основное уравнение динамики вращательного движения тела вокруг неподвижной оси. Оно аналогично уравнению второго закона Ньютона (основного уравнения динамики поступательного движения). Роль массы выполняет момент инерции тела, роль силы – момент силы, роль линейного ускорения – угловое ускорение. Момент инерции тела относительно оси является мерой инертности тела к изменению его угловой скорости. Чем больше момент инерции тела, тем труднее изменить ее скорость. При одном и том же значении момента силы тело с большим значением момента инерции приобретает меньшее угловое ускорение.

5.5. Вычисление моментов инерции. Теорема Штейнера

Момент инерции твердого тела зависит от массы и ее распределения относительно оси вращения. Вычисление момента инерции сводится к суммированию в случае дискретного распределения массы:

,

где - радиус вращения массы вокруг оси OZ.

При непрерывном распределении массы в объеме V суммирование должно быть заменено интегрированием по формулам:

, (5.21)

где - плотность материала, - радиус вращения элемента объема , имеющего массу .

Рассмотрим несколько примеров расчета момента инерции для тел простейшей формы относительно оси, проходящей через центр масс.

1) Момент инерции кольца, обруча или тонкостенного цилиндра массы m и радиуса R.

В

Рис.5.7

се малые элементы тела находятся на одном и том же расстоянии от его оси, проходящей через центр масс (рис.5.7). Поэтому

. (5.22)

2) Момент инерции диска или сплошного однородного цилиндра массы m и радиуса R относительно его оси.

В

Рис.5.8

нутри диска выделим тонкое кольцо радиуса r толщиной dr и шириной, равной ширине диска h (рис.5.8). Объем и масса такого кольца равны:

и ,

где ρ – плотность диска.

Момент инерции рассматриваемого элемента равен

,

а всего диска

. (5.23)

Ввиду однородности диска его масса равна

.

С учетом этого окончательно, получим

. (5.24)

А

Рис.5.9

налогично, момент инерции полого толстостенного цилиндра (рис.5.9) с внешним радиусом R₂ и внутренним R₁ можно представить в виде интеграла (5.23), но пределы интегрирования считать равными R₁ и R₂:

. (5.25)

С учетом того, что масса полого цилиндра равна

,

имеем

. (5.25)

3) Момент инерции однородного тонкого стержня массы m и длины l относительно оси, проходящей перпендикулярно стержню через его середину.

Р

Рис.5.10

азобьем стержень на элементарные отрезки dx (рис.5.10). Тогда

,

где ρ – плотность стержня, приходящаяся на единицу его длины.

Момент инерции всего стержня находим, интегрируя данное выражение в пределах от 0 до , с последующим его удвоением

.

Так как , то

. (5.26)

4

Рис.5.11

). Момент инерции шара массы m и радиуса R относительно оси OZ.

Выделим тонкий диск радиуса r и толщиной dz, удаленный от центра шара на расстояние z (рис.5.11). Масса этого диска равна

,

где - плотность шара, а .

Момент инерции данного диска определяется формулой

.

Момент инерции шара найдем интегрированием по z в пределах от 0 до R, с последующим удвоением результата, в силу симметрии задачи

.

Вводя в данную формулу массу шара, равную

,

получим окончательно

. ( 5.27)

Р

Рис.5.12

асчет момента инерции тела относительно произвольной оси облегчается, если использовать теорему Штейнера. В соответствии с этой теоремой, момент инерции относительно произвольной оси равен сумме моментов инерции тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между этими осями

. (5.28)

В качестве примера, рассчитаем момент инерции стержня относительно оси перпендикулярной стержню и проходящей через его конец (рис.7.12). По теореме Штейнера будем иметь

. (5.29)