4.7.3 Корпускулярно-волновой дуализм. Волны де Бройля

Недостаточность теории Бора указывала на необходимость пересмотра основ квантовой теории и представлений о природе микрочастиц (электронов, протонов и т. п.). Возник вопрос о том, насколько исчерпывающим является представление электрона в виде малой механической частицы, характеризуемой определенными координатами и определенной скоростью.

В результате углубления представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм. Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (интерференция, дифракция), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, явление Комптона).

В 1924 г. Луи де Бройль предположил, что частицы вещества, наряду с корпускулярными свойствами, имеют также и волновые свойства. По идее де Бройля, движение электрона или какой-либо другой частицы со скоростью v и массой m, связано с волновым процессом, длина волны которого равна

λ = 2πћ/p =2πћ/mv

(4.91).

Рассмотрим свободно движущуюся со скоростью v частицу массой т. Вычислим для нее фазовую и групповую скорости волн де Бройля. Фазовая скорость

v = ω/k = ђω/ђk = E/p = mc2/mv = c2/v

(4.92).

Так как c>v, то фазовая скорость волн де Бройля больше скорости света в вакууме (фазовая скорость волн может быть как меньше, так и больше с в отличие от групповой скорости волн. Групповая скорость

u = dω/dk = d (ђω)/d(ђk) = dE/dp

Для свободной частицы Е =√m₀²c⁴+p²с² и

dE/dp = pc2/√m02c4+p2с2 = pc2/E = mvc2/mc2 = v

(4.93).

Следовательно, групповая скорость волн де Бройля равна скорости частицы. Групповая скорость фотона u = pc²/E = mcc²/mc² = c, т. е., равна скорости самого фотона.

Волны де Бройля испытывают дисперсию, так как скорость распространения частицы – фазовая скорость, зависит от длины волны, т.е., волны де Бройля распространялись с разной скоростью.

Амплитуду волны де Бройля Борн предложил рассматривать как амплитуду вероятности нахождения частицы в некотором месте пространства. Вероятностный характер волн де Бройля отчетливо подтвердился в опытах по дифракции электронов при очень малой интенсивности пучка. Невозможно было предсказать заранее место попадания на фотопластинку отдельного электрона. Но, в конце концов, число рассеянных электронов и их распределение все меньше и меньше отличается от закона распределения вероятности. Волновая функция указывает вероятность найти эту частицу в разных точках пространства.

После этих опытов стало очевидно, что «классические» частицы обладают явно выраженными волновыми свойствами. Волны де Бройля распространяются, интерферируют и дифрагируют по обычным оптическим законам.

Гипотеза де Бройля вскоре была подтверждена экспериментально. Дэвиссон и Джермер исследовали в 1927 г. отражение электронов от монокристалла никеля. Узкий пучок моноэнергетических электронов направлялся на поверхность монокристалла. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру (рисунок - 4.74). Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. Варьировались скорость электронов и угол θ.

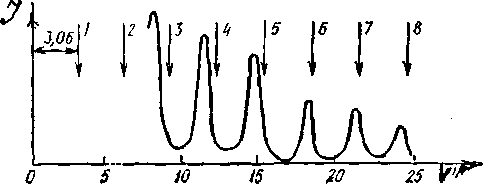
Прошедшие через отверстие в электроде ускоренные электроны попадали на кристалл С и рассеивались. При помощи детектора D измерялась интенсивность рассеянных электронов как функция угла θ при различных значениях ускоряющего потенциала, т. е. при различных энергиях электронов. На рисунке - 4.75 показана зависимость силы тока, измеряемой гальванометром, от угла θ при различных энергиях электронов. Кривые на рисунке являются типичными для распределения интенсивности при рассеянии волн. Максимумы и минимумы интенсивности почти равноудалены друг от друга. Такие же дифракционные максимумы и минимумы возникают при рассеянии рентгеновских лучей на кристаллах. Произведем расчеты для этого опыта. Кинетическая энергия Т электронов, ускоренных разностью потенциалов U, равна еU. Соответствующая длина волны де Бройля: λ = 2πћ/mv = 2πћ√/mU_e = 1,6А. Такую же длину волны (по порядку величины) имеют рентгеновские лучи. Неудивительно поэтому, что дифракционная картина для электронов оказывается очень похожей на дифракционную картину при рассеянии рентгеновых лучей на тех же кристаллах.

Рисунок - 4.74	Рисунок - 4.75

Положение максимумов при отражении от кристалла, как известно, определяется формулой Брэгга — Вульфа 2d cos θ = nλ Подставляя в эту формулу найденную длину волны электронов вычислим, что максимумы на рисунке 10 должны наблюдаться при √U = nπћ/√2m_e d cos θ, где п — любое целое число. Полученные таким путем U (стрелки указывают расчетные положения максимумов 3-го, 4-го, 5-го и т. д. порядков), свидетельствует о том, что теория де Бройля правильно описывает картину рассеяние электронов, полученные из эксперимента. Проверка формулы и лежащей в ее основе формулы, проведенная по положению пиков другими методами, показала справедливость этих формул.

Через некоторое время после опытов Дэвиссона и Джермера были поставлены опыты, в которых дифракция электронов наблюдалась при пропускании электронов через тонкие металлические пластинки (Томсон, Тартаковский). Электрон при ударе о фотопластинку оказывает на нее такое же действие, как и фотон. Полученная таким способом электронограмма была сопоставлена с полученной, в аналогичных условиях, рентгенограммой алюминия. Сходство обеих картин было поразительно. Количественный анализ результатов опытов полностью подтвердил правильность уравнений де Бройля.

Описанные выше опыты производились с пучками частиц. Поэтому возникает вопрос: волновые свойства, проявления которых наблюдались в этих опытах, являются свойствами пучка частиц или свойствами отдельных частиц? Иначе говоря, не являются ли наблюдаемые в этих опытах волновые свойства результатом взаимодействия частиц друг с другом? Физики Л М. Биберман, Н.Г. Сушкин и В. А. Фабрикант осуществили в 1949 г. опыт, в котором интенсивность электронного пучка была настолько слабой, что электроны проходили через прибор заведомо поодиночке. Промежуток времени между двумя последовательными прохождениями электронов через кристалл примерно в 30 000 раз превосходил время, затрачиваемое электроном на прохождение всего прибора. При достаточной экспозиции была получена дифракционная картина, ничем не отличающаяся от той какая наблюдается при обычной интенсивности пучка. Таким образом, было доказано, что волновые свойства присущи отдельному электрону.

Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у других элементарных частиц. Длина волны де Бройля обратно пропорциональна массе частицы. Следовательно, при той же скорости длина волны нейтрона или некоторой молекулы в тысячи раз меньше, чем длина волны электрона. Для успешного наблюдения дифракции волн на кристаллах необходимо, чтобы длина волны была порядка расстояний между узлами кристаллической решетки. Поэтому для наблюдения дифракции тяжелых частиц необходимо пользоваться частицами с малыми скоростями.

В случае нейтронов можно пользоваться «тепловыми» нейтронами, т. е. нейтронами, находящегося при комнатной температуре, т. е. при температуре около 300° К. Нетрудно подсчитать, что при этих энергиях длина волны нейтрона имеет порядок 1 А, т. е. такие нейтроны пригодны для осуществления опытов по дифракции на кристаллах.

Опыты с нейтронными и молекулярными пучками полностью подтвердили уравнения де Бройля в применении к тяжелым частицам. Благодаря этому было доказано, что волновые свойства являются универсальным свойством микрочастиц. Они не обусловлены особенностями внутреннего строения той или иной частицы, а отражают общий закон движения материальных частиц.

При объяснении всех этих опытов возможно предположение, что система интерференционных колец порождается не рассеянными электронами, а вторичными рентгеновыми лучами, возникающими в результате удара пучка электронов на пластинку. Для того чтобы убедиться, что это предположение неверно, на пути рассеянных лучей, между металлической пластинкой и фотопластинкой создается дополнительное магнитное поле. Оно не влияет на движение рентгеновых лучей и, следовательно, не должно искажать интерференционной картины, если она порождается рентгеновыми лучами. Если же интерференционная картина порождается рассеянными электронами, то дополнительное магнитное поле должно исказить эту картину. Такого рода проверка при наблюдении дифракции по методу Дебая — Шерера показала, что дифракционная картина обусловливается именно рассеянными электронами, а не вторичными рентгеновыми лучами.

Вся совокупность изложенных в этой главе экспериментальных фактов говорит о том, что все микрочастицы обнаруживают как корпускулярные, так и волновые свойства, а уравнения де Бройля имеют всеобщую значимость и отражают общий закон природы.

То обстоятельство, что электроны наряду е корпускулярной природой обладают и волновыми свойствами, привел исследователей к мысли об использовании здесь далеко идущих аналогий их с фотонами для различных научных и практических целей. Особенно важным является то, что длина волны де Бройля оказывается значительно меньше длины световых волн, что позволяет строить электронно-оптические приборы гораздо более высокой разрешающей силы, нежели оптические микроскопы.

Согласно теории, разрешающая способность микроскопа пропорциональна длине волны, а так как длина волны применяемых электронных пучков (примерно 1 пм) в тысячи раз меньше длины волны световых лучей, то разрешение электронных микроскопов соответственно больше и составляет 0,01 — 0,0001 мкм (для оптических микроскопов приблизительно равно 0,2—0,3 мкм). С помощью электронных микроскопов можно добиться значительно больших увеличений (до 10⁶раз), что позволяет наблюдать детали структур размерами 0,1 нм.

Указанное обстоятельство широко используют в электронном микроскопе. Электронный микроскоп представляет собой устройство, содержащее источник электронов, пропускаемых через исследуемый объект (или отражаемых от него), систему электрических или магнитных линз, люминесцирующий экран, светящийся под действием электронов, дополнительную оптическую систему, позволяющую рассматривать изображение объекта на экране, и другую аппаратуру.