1.2.3 Работа сил в механике, энергия. Закон сохранения энергии в механике

Работой постоянной силы F, когда тело движется поступательно и прямолинейно, при прохождении телом пути S, называют величину

А = FScos α = FτS,

(1.90),

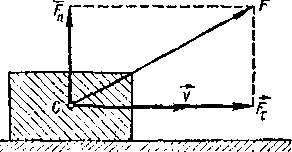
где α— угол между силой F и направлением движения тела. Здесь. F_τ= Fcos α — проекция силы F на направление вектора v скорости тела (рисунок - 1.30).

В общем случае тело может двигаться произвольным, достаточно сложным образом, а сила F — изменяться (рисунок - 1.31). Тогда, рассматривая достаточно малое (элементарное) перемещение тела ds, в пределах которой можно считать силу F постоянной, элементарную работу, можно вычислить по формуле:

dА = Fcosαds = Fτds

(1.91).

Работа, совершаемая силой F на конечном пути s, равна сумме элементарных работ на отдельных бесконечно малых участках пути; эта сумма приводится к интегралу:

A = ∫F cos αds = ∫Fτ ds

(1.92).

Работа, совершаемая силой F на конечном пути S, графически измеряется площадью заштрихованной на рисунке - 1.31 фигурой, ограниченной, с одной стороны функцией F(t), с другой стороны, ординатами, определяемыми S.

Рисунок - 1.30	Рисунок - 1.31

Силу F, действующую на материальную точку, называют консервативной, или потенциальной, если работа А, совершаемая этой силой при перемещении точки из одного произвольного положения в другое, не зависит от того, по какой траектории это перемещение произошло. Поэтому при перемещении материальной точки вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Таким образом, консервативные силы можно определить двумя способами:

1) как силу, работа которой не зависит от пути, по которому частица переходит из одного положения в другое;

2) как силу, работа которой по замкнутому пути равна нулю.

Примерами консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия между заряженными телами.

Все силы, не удовлетворяющие условию консервативности, называются неконсервативными. Характерным примером таких сил являются силы трения скольжения. Сила трения скольжения всегда направлена в сторону, противоположную направлению движения, так чтоcosα = -1. Поэтому работа силы трения скольжения вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.

Для характеристики скорости совершения работы силой вводится понятие мощности. Мощностью N силы F называется физическая величина, численно равная работе, совершаемой этой силой за единицу времени:

N = dA/dt

(1.93.

Подставляя в эту формулу выражение для элементарной работы, получим

N = F cosα ds/dt = Fvcosα

(1.94),

где v — скорость точки приложения силы.

В механике различают два вида энергии, кинетическую и потенциальную. Кинетической энергией тела называют энергию Е_K, являющуюся мерой его механического движения и измеряемую той работой, которую может совершить тело при его торможении до полной остановки. Найдем выражение для кинетической энергии твердого тела В, имеющего массу т и движущегося поступательно со скоростью v.

Пусть тело В тормозится под действием некоторой силой F (в общем случае переменной) и на малом участке пути ds совершает элементарную работу dА = - F_τ ds. По второму закону Ньютона - F_τ= mdv/dt Следовательно, dA = - m (dv/dt) ds = - m (ds/dt) dv = - m v dv. Работа, совершаемая телом В до полной его остановки

A = - ∫ m v dv = mv2/2

(1.95).

Итак, кинетическая энергия поступательно движущегося телa, равна половине произведения массы этого тела на квадрат его скорости:

Ек = A = mv2/2

(1.96).

Данная формула справедлива для кинетической энергии материальной точки. Любую механическую систему можно рассматривать как систему материальных точек. Поэтому кинетическая энергия Е_K механической системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему:

Ек = ∑ Еi = ∑mivi2/2

(1.97),

где m_i, v_i — масса и скорость i-й материальной точки. Таким образом, кинетическая энергия системы полностью определяется величинами масс и скоростей движения. входящих в нее материальных точек. Она не зависит от того, каким образом части рассматриваемой системы приобрели данные значения скоростей. Кратко этот важный вывод можно сформулировать следующим образом: кинетическая энергия системы есть функция состояния ее движения.

Если на систему материальных точек или тел действуют консервативные (потенциальные) силы, то можно ввести понятие потенциальной энергии этой системы. В самом деле, работа, совершаемая консервативными силами, не зависит от того, как было осуществлено это перемещение. Работа А_1-2 при перемещении системы из одной точки пространства, полностью определяется начальной и конечной местоположениями системы. Это можно выразить в форме

А1-2 = Еп1 – Еп2

(1.98),

где Еп — некоторая функция состояния системы, зависящая только от координат всех материальных точек системы. Эту функцию называют потенциальной энергией системы. Отсюда следует, что работа консервативных сил, действующих на механическую систему, равна убыли потенциальной энергии этой системы. Из определения следует, что потенциальная энергия системы в произвольном состоянии равна работе, совершаемой консервативными силами при переводе системы из одного состояния в другое по условию задачи.

Так, например, работа силы тяжести зависит только от разности высот начальной и конечной точек пути. Сила тяжести тела приложена к его центру тяжести. Поэтому работа силы тяжести при любом движении тела равна произведению этой силы на разность высот начального и конечного положений его центра тяжести. Отсюда следует, что работа силы тяжести вдоль замкнутой траектории центра тяжести тела равна нулю, т. е. что сила тяжести, действительно, является консервативной. Потенциальная энергия тела, поднятого на высоту H над поверхностью Земли равна

En =mgH+ Еno

(1.99),

где Е_n0— потенциальная энергия тела, лежащего на поверхности Земли. Обычно принимают Е_n0 = 0, так что

Еn = mgH.

(1.100).

Найдем потенциальную энергию упруго деформированного тела. Сила упругости F_ynp, как известно из опыта, пропорциональна величине деформации х, т. е. F_ynp, = - kх где k — коэффициент упругости, характеризующий упругие свойства тела, а знак минус показывает, что сила упругости направлена в сторону, противоположную направлению деформации: упруго деформированное тело стремится восстановить свои первоначальные форму и размеры.

Элементарная работа, совершаемая силой F_ynp при бесконечно малом изменении деформации тела на величину dx равна dА = (F_ynpdx) = - kxdx. Работа этой силы при конечном изменении деформации тела, например, при переводе его из недеформированного состояния (х=0) в состояние, соответствующее деформации х, равна

А = - ∫kxdx = - kx2/2

(1.101).

Работа А не зависит от хода процесса деформации тела и полностью определяется значениями деформации тела в начальном и конечном состояниях. Следовательно, силы упругости являются консервативными, а потенциальная энергия упруго деформированного тела

Еn = kx2/2.

(1.102).

Полной механической энергией системы называют величину E, равную сумме кинетической и потенциальной энергий этой системы:

E = EK+ En.

(1.103).

Полная механическая энергия системы — функция ее состояния, так как зависит только от координат, скоростей и масс всех малых частей (материальных точек) системы

Найдем условие, которому должна удовлетворять система тел для того, чтобы ее полная механическая энергия не изменялась с течением времени. Если v — скорость i-й материальной точки с массой т_и то ее кинетическая энергия E_кi = m_iv_i²/2. Изменение этой энергии за малый промежуток времени dt, связанное с изменением скорости v, на dv_i= a_idt (а_i— ускорение рассматриваемой материальной точки), равно

dEкi = mi /2[(dvi, vi) + (vi ,dvi,)] = mi(aidt, vi,) = (miаi, vtdt) = (miаi, dri)

(1.104),

где dr_i = v_idt— приращение радиуса-вектора r_i, материальной точки. По второму закону Ньютона m_iа_i = F_i + f_i, где F_i и f_i — результирующие, соответственно, консервативных и неконсервативных сил, действующих на i-ю материальную точку. Поэтому

dEкi. = (Fi dri) + (fi dri)

(1.105).

Кинетическая энергия W_K всей системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему, а ее изменение за малый промежуток времени dt dЕ_к = ∑dE_кi., т. е.

dЕк =∑(Fi dri) +∑(fi dri)

(1.106).

Первая сумма в правой части этого уравнения представляет собой суммарную работу dA, совершаемую всеми консервативными силами за промежуток времени dt. Эта работа равна убыли за то же время dt потенциальной энергии системы

Еn = Еnвнутр + Еnвнешн

(1.107),

∑(Fi dri) = dA = - dЕn

(1.108).

Вторая сумма в правой части уравнения ∑(f_i dr_i).представляет собой суммарную работу dA_нк, совершаемую всеми неконсервативными силами. Таким образом, уравнение можно переписать в форме dЕ_к + dЕ_n = dA_нк, или

dЕ = dAнк,

(1.109),

где Е= Е _K+ Е _n — полная механическая энергия системы.

Если внутренние силы взаимодействия между которыми консервативны, а все внешние силы — стационарны и консервативны, такую систему тел (материальных точек) называют консервативной системой,. Для такой системы dA = dE = 0 и

E = EK+ Eп= const,

(1.110),

т. е. полная механическая энергия консервативной системы не изменяется с течением времени. Этот закон называют законом сохранения механической энергии. Он справедлив, для замкнутой консервативной системы, т е системы, на которую внешние силы не действуют, а все внутренние силы — консервативны.

Рассмотрим применение закона сохранения механической энергии к расчету абсолютно упругого прямого центрального удара двух тел. Абсолютно упругим называют такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии. Пусть два абсолютно упругих шара с массами m₁ и m₂ до удара (рисунок - 1.32, а) движутся поступательно со скоростями v₁ и v₂, направленными в одну и ту же сторону вдоль линии их центров, причем v₁ > v₂. Нужно найти скорости шаров u₁ и u₂ после соударения (рисунок - 1.32, б).

Рисунок - 1.32

В процессе удара систему соударяющихся тел можно считать замкнутой. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, т. е. потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем

m1v12/2 + m2v22/2 = m1u12/2 + m2u22/2

(1.111),

где u₁ и u₂ скорости этих шаров после соударения. По закону сохранения импульса

m1v1 + m2v2 = m1u1 + m2u2

(1.112).

Совместное решение двух последних уравнений дает

u1 = [v1(m1-m2)+ 2m2v2] / (m1+m2), u2 = [v2(m2-m1)+ 2m1v1] / (m1+m2)

(1.113),

т.е., после упругого соударения тела двигаются каждая со своей скоростью кинетической энергией Е₁ и Е₂ соответственно.

Систему тел называют диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс называют процессом диссипации (рассеяния) энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся тел.

При абсолютно неупругом ударе происходит диссипация энергии. Изменение ∆E полной механической энергии системы соударяющихся тел равно изменению их кинетической энергии

∆E = ∆Eк =(m1+m2)u2/2 - [m1v12/2 + m2v22/2]

(1.114).

Общую скорость тел можем найти, применяя закон сохранения импульса для неупругого удара, учитывая, что после соударения они двигаются вместе, имея общую скорость:

u = (m1v1 + m2v2)/ (m1+m2)

(1.115.

После преобразований, рассеянная энергия равна:

∆E =- m1m2 (v1 –v2)2 /2(m1+m2)

(1.116).