3.1.3 Теорема Остроградского — Гаусса и его применение для расчета полей

Теорема Остроградского — Гаусса связывает поток силовых линий через произвольную замкнутую поверхность с электрическим зарядом, находящимся внутри этой поверхности. Для замкнутой поверхности условились считать положительным направление нормали, выходящее из объема, ограничиваемого поверхностью. Тогда силовые линии, выходящие из объема, ограниченного данной поверхностью, создают положительный поток; линии же, входящие в объем, создадут отрицательный поток.

Найдем поток, образованный точечным зарядом q и пронизывающий замкнутую сферическую поверхность, окружающую этот заряд и имеющую центр в точке нахождения заряда (рис. 28,а). Напряженность в точках поля, лежащих на сфере радиуса r вокруг точечного заряда q в среде с диэлектрической проницаемостью ε, равна

E = q /4πε0 εr2

(3.9).

В данном случае проекция напряженности на направление внешней нормали (радиуса) равна напряженности поля. Вследствие этого поток, пронизывающий сферу в вакууме (ε= 0), равен

ФЕ =( q /4πε0 εr2) 4πr2 = q/ε0

(3.10).

Знак потока совпадает со знаком заряда q. Из данного результата следует, что поток силовых линий, пронизывающих сферу, не зависит от ее радиуса. Заменим сферу, окружающую точечный заряд, произвольной замкнутой поверхностью S₁ (рис. 28,6). На основании свойства непрерывности силовых линий можно утверждать, что поток, образованный точечным зарядом и пронизывающий произвольную замкнутую поверхность, внутри которой находится этот заряд, будет таким, как и в случае сферической поверхности, окружающей заряд: Ф_Е = q/ε₀. Если замкнутая поверхность не охватывает заряд (S₂ на рисунке - 3.7,б), то поток силовых линий через эту поверхность равен нулю, так как число силовых линий, входящих через поверхность, равно числу силовых линий, выходящих из нее.

Рисунок – 37

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд q, поток вектора Е будет равен q/ε₀, т. е.

ФЕ = ∫EndS,= q/ε0

(3.11).

В общем случае внутри замкнутой поверхности может находиться любое число n зарядов. Поток, создаваемый зарядом q_k, будет 4π q_k/ε, при этом знак потока совпадает со знаком заряда и равен алгебраической сумме потоков отдельных зарядов:

∫EndS = ∑ q/ε0

(3.12),

где ∫— интеграл по замкнутой поверхности S. Данная формула выражает теорему Остроградского—Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность пропорционален алгебраической сумме всех зарядов, расположенных внутри поверхности. Рассчитаем с помощью теоремы Остроградского — Гаусса электрические поля в ряде частных случаев. Для простоты будем рассматривать поля в вакууме.

Напряженность поля равномерно заряженной бесконечной плоскости. Пусть электрическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью заряда +σ =d q/dS (рисунок - 3.8,а). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей.

Так как образующие цилиндра параллельны линиям напряженности (cos α = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания E совпадает с E_n), т.е. равен 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Остроградского — Гаусса, 2ES = σS/ε₀, откуда

E = σ/(2ε0).

(3.13).

Из формулы (3.13) следует, что E не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

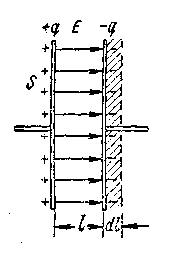
Поле двух бесконечных параллельных разноименно заряженных плоскостей (рисунок - 3.8,б). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и -σ Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля Е = 0. В области между плоскостями Е = Е⁺ + Е^- (Е⁺ и Е^- напряженности от соответствующих знакам зарядов плоскостей. Поэтому результирующая напряженность

Е= σ/ε0.

(3.14).

Таким образом, результирующая напряженность поля между плоскостями описывается полученной формулой, а вне объема, ограниченного плоскостями, равна нулю.

Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью +σ (рисунок - 3.8,в). Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально.

а)	б)	в)
Рисунок - 3.8

Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле, и, по теореме Остроградского-Гаусса, 4πr²E = q/ε₀, откуда

E = q/4πr2ε0 (r›R).

(3.15).

При r‹R поле убывает с расстоянием по такому же закону, как у точечного заряда. Если r<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).

Поле равномерно заряженного бесконечного цилиндра (нити). Предположим, что бесконечный цилиндр радиуса R равномерно заряжен так, что на единицу его длины приходится заряд τ= q/l (рисунок - 3.9). Из условия симметрии следует, что силовые линии будут радиальными прямыми, перпендикулярными к поверхности цилиндра. Выберем в качестве замкнутой поверхности поверхность прямого цилиндра с радиусом оснований r > R и осью, совпадающей с осью заряженного цилиндра. Высота этого цилиндра равна l (рисунок - 3.9).

Рисунок - 3.9	Рисунок - 3.10

Поток силовых линий через основание выбранного цилиндра равен нулю. Силовые линии перпендикулярны к боковой поверхности цилиндра, поэтому поток напряженности через замкнутую цилиндрическую поверхность равен 2πrlE. По теореме Остроградского — Гаусса при r > R, 2πrlE = τl/ε₀ откуда

E = τ/2πr ε0

(3.16).

Если r<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри выбранного цилиндра электростатическое поле отсутствует (Е = 0).