1.3.2 Кинетическая энергия вращательного движения. Момент инерции

Кинетическая энергия вращающегося тела равна сумме кинетических энергий всех частиц тела:

Eк = ∑mivi2/2

(1.124),

где т_i-— масса какой-либо частицы, а v_i— ее линейная скорость, пропорциональная расстоянию r_i данной частицы от оси вращения. Подставляя в это выражение v_i= ωr_i и вынося за знак суммы общую для всех частиц угловую скорость ω, находим:

Eк = ω2/2∑miri2

(1.125).

Эту формулу для кинетической энергии вращающегося тела можно привести к виду, аналогичному выражению кинетической энергии поступательного движения, если ввести величину момента инерции тела. Моментом инерции материальной точки называют произведение массы точки на квадрат расстояния от оси вращения:

Ii = miri2

(1.126).

С использованием понятия момента инерции кинетическая энергия вращающегося тела определяется такой формулой:

Е = Iω2/2

(1.127).

Сравнивая формулы кинетической энергии тела при поступательном и вращательном движении, находим, что роль массы тела во вращательном движении играет момент инерции I. Отсюда следует, что момент инерции играет ту же роль, что и масса для поступательного движения, как меры инертности.

Зная формулу момента инерции материальной точки, можно вычислить момента инерции любого тела. Для того необходимо дифференцировать тело на такие маленькие кусочки dm, когда их можно принять материальной точкой: это позволяет применить к ним соответствующую формулу dI_i = r_i²dm_. Тогда момент инерции тела можно вычислить как сумму моментов инерции всех точек, образующих это тело:I = ∑m_ir_i². Или, учитывая, что тело является сплошной средой, математически можно вычислить через интеграл:

I = ∫miri2

(1.128).

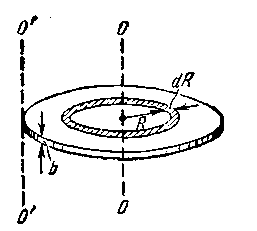
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рисунок - 1.37). Разобьем диск на кольцевые слои толщиной dR. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном R. Объем такого слоя равен dV=b2πRdR, где b — толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова и ρ в уравнении можно вынести за знак интеграла: I = ρ∫R²dV = ρ∫R²b2nRdR, где R— радиус диска. Вынесем за знак интеграла постоянный множитель 2πb: I=2πbρ∫ R² dR = 2πbρ R⁴/4. Наконец, введя массу диска т, равную произведению плотности р на объем диска bπR², получим:

I = mR2/2

(1.129).

Рисунок - 1.37

Если необходимо найти момент инерции диска относительно, любой оси например, оси О'О' (рисунок - 1.37), вычисления оказываются более сложными. Нахождение момента инерции значительно облегчается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси равен сумме момента инерции I_c относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния а между осями:

1 = 1с + та2

(1.130).

Теорема Штейнера сводит вычисление момента инерции относительно любой произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела. Ниже приводятся моменты инерции некоторых однородных тел простейшей формы (таблица - 1.1). Полученные данные показывают, что момент инерции тела зависит не только от его массы, но и от ее распределения относительно оси вращения.

Таблица - 1.1 Моменты инерции некоторых тел

Тело	Положение оси О	Момент инерции
Полый тонкостенный цилиндр радиуса R, массой m	Ось симметрии	Jо = mR2
Сплошной цилиндр (или диск) радиуса R, массой m	Ось симметрии	Jо = mR2/2
Прямой тонкий стержень, длиной l и массой m	Ось перпендикулярна к стержню и проходит через его середину	Jо = ml2/12
Тот же стержень	Ось перпендикулярна к стержню и проходит через его конец	Jо = ml2/3
Шар радиуса R, массой m	Ось проходит через центр шара	Jо = 2mR2/5