4.3.3 Дифракция в параллельных лучах

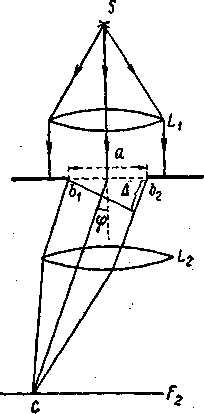
Схема наблюдения дифракции Фраунгофера изображена на рисунке - 4.33. Точечный источник света S расположен в главной фокальной плоскости линзы L₁. Из линзы L₁ выходит параллельный пучок лучей, на пути которого расположен непрозрачный экран с отверстием b₁b₂. Экран частично загораживает пучок лучей, который затем падает на вторую линзу L₂. В случае прямолинейного распространения света лучи распространялись бы и за экраном параллельным пучком и были бы собраны второй линзой L₂ в точку в ее главной фокальной плоскости (обе линзы считаем идеальными). На самом деле в фокальной линзы L₂ наблюдается дифракционная картина, вид которой зависит от формы и размеров отверстия в экране и длины падающей волны.

Рассмотрим частные случаи дифракции Фраунгофера.

Дифракция на одной щели. Влияние ширины щели на дифракционную картину. Пусть на щель b₁b₂ шириной а (рисунке - 4.33) падает пучок параллельных лучей. Щель считаем бесконечно протяженной в направлении, перпендикулярном к плоскости рисунка. За щелью расположена линза L₂, собирающая лучи в главной фокальной плоскости. Лучи, идущие под некоторым углом φ к первоначальному направлению, соберутся в фокальной плоскости линзы L₂ в точке С. Оптическая разность хода между крайними лучами, идущими от щели в произвольном направлении φ: ∆ = a sin φ

Для подсчета амплитуды колебаний в точке С разобьем волновой фронт на зоны в виде узких полосок одинаковой ширины, параллельных краям щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т. е. всего на ширине щели уместится ∆: λ/2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с фронтом волны; следовательно, все точки фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения:

a sin φ = ±2k λ/2 (k=1, 2, 3, )

(4.53).

Число зон Френеля, укладывающихся на ширине щели, зависит от угла φ, От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Если число зон Френеля четное то в точке C наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное то наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в прямом направлении (φ = 0) щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в этой точке наблюдается центральный дифракционный максимум:

a sin φ= ± (2k + 1) (т = 1, 2, 3,)

(4.54).

Из вышеназванных условий можно найти направления на точки экрана, в которых амплитуда (а следовательно, и интенсивность) равна нулю (sin φ_mjn=±kλ/а) или максимальна (sinφ_max = ±(2k+1)λ/(2а). Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр), приведено на рисунке - 4.34.

Рисунок - 4.33	Рисунок - 4.34

Расчеты показывают, что интенсивности центрального и последующих максимумов относятся как 1:0,047:0,017:0,0083:, т. е. основная часть световой энергии сосредоточена в центральном максимуме.

Положение дифракционных максимумов зависит от длины волны λ, поэтому рассмотренный вид дифракционной картины имеет место лишь для монохроматического света. При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех длин волн (при φ = 0 разность хода равна нулю для всех λ). Боковые максимумы радужно окрашены, так как условие максимума при любых т различно для разных λ. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (k=1), второго (k=2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.

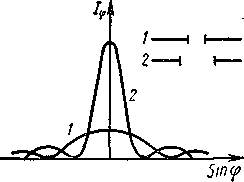
Рассмотрим влияние ширины щели на дифракционную картину. Как следует из рисунка - 4.35, с увеличением ширины щели происходит сближение максимумов и минимумов относительно центра. Поскольку с увеличением ширины щели увеличивается общий световой поток, то интенсивность при сравнительно больших отверстиях должна быть больше. На рисунке 4.35 представлен график распределения интенсивности для щелей разной ширины.

Как видно из рисунка, с уменьшением ширины щели центральный максимум расплывается. При b=λ (что соответствует sin φ=1, т. е. φ=π/2) центральный максимум расплывается в бесконечность, что приводит к равномерному освещению экрана. Дальнейшее уменьшение ширины щели (b <λ) приводит к отклонению от теории Френеля-Кирхгофа. Этот случай не имеет смысла с практической точки зрения, так как при этом наблюдается монотонное уменьшение интенсивности прошедшего света.

Увеличение ширины щели (b>λ) приводит к сужению центрального максимума и увеличению яркости. При b<λ мы получаем в центре резкое изображение источника света, т. е. имеет место прямолинейное распространение света.

Дифракция на двух щелях. Положение дифракционных максимумов и минимумов не будет зависеть от положения щели, ибо положение максимумов определяется направлением, по которому идет большая часть испытавшего дифракцию света. Поэтому при перемещении щели параллельно самой себе никаких изменений дифракционной картины не должно наблюдаться. Если в непрозрачной перегородке проделаны две идентичные параллельные щели, то они дадут одинаковые накладывающиеся друг на друга дифракционные картины вследствие чего максимумы соответственным образом усилятся. Однако в действительности картина окажется сложнее, ибо надо принять в расчет взаимную интерференцию волн, идущих от первой и второй щелей.

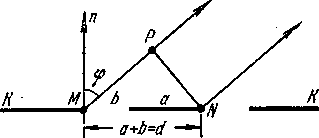
Предположим, что мы прорезали в перегородке КК (рисунок - 4.36) две щели шириной b, разделенные непрозрачным промежутком а, так что а + b = d.

Рисунок - 4.35	Рисунок - 4.36

К определению положения главных максимумов и добавочных минимумов при дифракции на двух параллельных щелях.

Очевидно, что минимумы будут на прежних местах, ибо те направления, по которым ни одна из щелей не посылает света, не получат его и при двух щелях. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются. Это будут, очевидно, направления, которым соответствует разность хода ½ λ, 3/2λ, для волн, идущих щелей. Такие направления определяются, как легко видеть из рисунка- 4.36, условием MP = MNsinφ = 1/2λ, 3/2λ, т. е.

dsinφ =1/2λ, 3/2λ

(4.55).

Наоборот, в направлениях, определяемых из условий действие одной щели усиливает действие другой, так что этим направлениям соответствуют главные максимумы:

dsinφ =λ, 2λ

(4.56).

Таким образом, полная картина определяется из условий:

- прежние минимумы: bsin φ = λ, 2λ, 3 λ;

- добавочные минимумы: dsinφ =1/2λ, 3/2λ, 5/2λ;

- главные максимумы: dsinφ = 0.

Таким образом, при дифракции Фраунгофера на двух щелях на экране, между двумя главными максимумами располагается один добавочный минимум.

Дифракционная решетка. Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. На рисунке - 4.37 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна a, а ширина непрозрачных участков между щелями b, то величина d=(a+b) называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки: ∆ = CF = (a + b) sin φ = d sin φ. Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут оставаться на своих местах:

a sin φ =±kλ (k=1, 2, 3, )

(4.57).

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы.

Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ/2, Зλ/2, , посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом условие дополнительных минимумов:

dsinφ=±(2k+l)λ/2 (k = 0, l, 2, )

(4.58).

Наоборот, действие одной щели будет усиливать действие другой, если

dsinφ=±2k λ/2 (k = 0, l, 2, )

(4.59),

т. е. это выражение задает условие главных максимумов.

Таким образом, полная дифракционная картина для двух щелей определяется из условия:

- главные минимумы: a sin φ = λ, 2λ, Зλ, ;

- дополнительные минимумы: d sin φ= λ/2, Зλ/2, λ/2, 5λ/2;

- главные максимумы: d sin φ=0, λ, 2λ,3λ , т. е. между двумя главными максимумами располагается один дополнительный минимум. Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех щелях — три и т. д.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов и условием главных максимумов сохраняются, а условием дополнительных минимумов будет следующим:

d sin φ= ±2k' λ/N (k'=l, 2, . N—l, N+l, , 2N—1, 2N+1, )

(4.60),

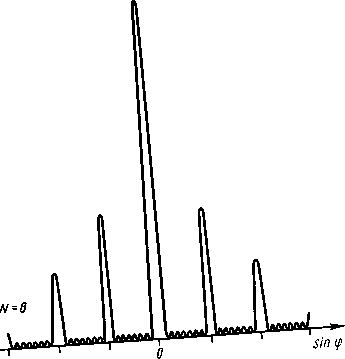
где k' может принимать все целочисленные значения, кроме 0, N, 2N,\ Следовательно, в случае N щелей между двумя главными максимумами располагается N-1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон. Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рисунке 4.38 представлена качественная дифракционная картина от восьми щелей.

Рисунок - 4.37	Рисунок - 4.38