- •Введение Физика как наука. Содержание и структура физики
- •I Механика
- •1.1 Кинематика материальной точки
- •1.1.1 Понятие материальной точки. Система отсчета. Траектория, путь, перемещение Единицы измерения
- •1.1.2 Скорость и ускорение произвольно движущейся точки
- •1.1.3 Кинематика прямолинейного движения
- •1.1.4 Движение точки по окружности. Связь между линейными и угловыми кинематическими параметрами
- •1.1.5 Колебательное движение. Виды гармонических колебаний
- •1.1.6 Сложение гармонических колебаний
- •1.2 Динамика материальной точки
- •1.2.1 Законы Ньютона. Масса, сила. Закон сохранения импульса, реактивное движение
- •1.2.2 Силы в механике
- •1.2.3 Работа сил в механике, энергия. Закон сохранения энергии в механике
- •1.3 Динамика вращательного движения твердых тел
- •1.3.1 Момент силы, момент импульса. Закон сохранения момента импульса
- •1.3.2 Кинетическая энергия вращательного движения. Момент инерции
- •II Раздел молекулярная физика и термодинамика
- •2.1 Основные положения молекулярно-кинетической теории газов
- •2.1.1 Агрегатные состояния вещества и их признаки. Методы описания физических свойств вещества
- •2.1.2 Идеальный газ. Давление и температура газа. Шкала температур
- •2.1.3 Законы идеального газа
- •2.2 Распределение Максвелла и Больцмана
- •2.2.1 Скорости газовых молекул
- •2.3. Первое начало термодинамики
- •2.3.1 Работа и энергия в тепловых процессах. Первое начало термодинамики
- •2.3.2 Теплоемкость газа. Применение первого начала термодинамики к изопроцессам
- •2.4. Второе начало термодинамики
- •2.4.1. Работа тепловых машин. Цикл Карно
- •2.4.2 Второе начало термодинамики. Энтропия
- •2.5 Реальные газы
- •2.5.1 Уравнение Ван-дер-Ваальса. Изотермы реального газа
- •2.5.2 Внутренняя энергия реального газа. Эффект Джоуля—Томсона
- •III Электричество и магнетизм
- •3.1 Электростатика
- •3.1.1 Электрические заряды. Закон Кулона
- •3.1.2 Напряженность электрического поля. Поток линий вектора напряженности
- •3.1.3 Теорема Остроградского — Гаусса и его применение для расчета полей
- •3.1.4 Потенциал электростатического поля. Работа и энергия заряда в электрическом поле
- •3.2 Электрическое поле в диэлектриках
- •3.2.1 Электроемкость проводников, конденсаторы
- •3.2.2 Диэлектрики. Свободные и связанные заряды, поляризация
- •3.2.3 Вектор электростатической индукции. Сегнетоэлектрики
- •3.3 Энергия электростатического поля
- •3.3.1 Электрический ток. Законы Ома для постоянного тока
- •3.3.2 Разветвленные цепи. Правила Кирхгофа. Работа и мощность постоянного тока
- •3.4 Магнитное поле
- •3.4.1 Магнитное поле. Закон Ампера. Взаимодействие параллельных токов
- •3.4.2 Циркуляция вектора индукции магнитного поля. Закон полного тока.
- •3.4.3 Закон Био—Савара—Лапласа. Магнитное поле прямого тока
- •3.4.4 Сила Лоренца Движение заряженных частиц в электрических и магнитных полях
- •3.4.5 Определение удельного заряда электрона. Ускорители заряженных частиц
- •3.5 Магнитные свойства вещества
- •3.5.1 Магнетики. Магнитные свойства веществ
- •3.5.2 Постоянные магниты
- •3.6 Электромагнитная индукция
- •3.6.1 Явления электромагнитной индукции. Закон Фарадея. Токи Фуко
- •3.6.2 Ток смещения. Вихревое электрическое поле Уравнения Максвелла
- •3.6.3 Энергия магнитного поля токов
- •IV Оптика и основы ядерной физики
- •4.1. Фотометрия
- •4.1.1 Основные фотометрические понятия. Единицы измерений световых величин
- •4.1.2 Функция видности. Связь между светотехническими и энергетическими величинами
- •4.1.3 Методы измерения световых величин
- •4.2 Интерференция света
- •4.2.1 Способы наблюдения интерференции света
- •4.2.2 Интерференция света в тонких пленках
- •4.2.3 Интерференционные приборы, геометрические измерения
- •4.3 Дифракция света
- •4.3.1 Принцип Гюйгенса—Френеля. Метод зон Френеля. Зонная пластинка
- •4.3.2 Графическое вычисление результирующей амплитуды. Применение метода Френеля к простейшим дифракционным явлениям
- •4.3.3 Дифракция в параллельных лучах
- •4.3.4 Фазовые решетки
- •4.3.5 Дифракция рентгеновских лучей. Экспериментальные методы наблюдения дифракции рентгеновских лучей. Определение длины волны рентгеновских лучей
- •4.4 Основы кристаллооптики
- •4.4.1 Описание основных экспериментов. Двойное лучепреломление
- •4.4.2 Поляризация света. Закон Малюса
- •4.4.3 Оптические свойства одноосных кристаллов. Интерференция поляризованных лучей
- •4.5 Виды излучения
- •4.5.1 Основные законы теплового излучения. Абсолютно черное тело. Пирометрия
- •4.5.2 Источники света
- •4.6 Действие света
- •4.6.1 Фотоэлектрический эффект. Законы внешнего фотоэффекта
- •4.6.2 Эффект Комптона
- •4.6.3 Давление света. Опыты Лебедева
- •4.6.4 Фотохимическое действие света. Основные фотохимические законы. Основы фотографии
- •4.7 Развитие квантовых представлений об атоме
- •4.7.1 Опыты Резерфорда по рассеянию альфа-частиц. Планетарно-ядерная модель атома
- •4.7.2 Спектр атомов водорода. Постулаты Бора
- •4.7.3 Корпускулярно-волновой дуализм. Волны де Бройля
- •4.7.4 Волновая функция. Соотношение неопределенности Гейзенберга
- •4.8 Физика атомного ядра
- •4.8.1 Строение ядра. Энергия связи атомного ядра. Ядерные силы
- •4.8.2 Радиоактивность. Закон радиоактивного распада
- •4.8.3 Радиоактивные излучения
- •4.8.4 Правила смещения и радиоактивные ряды
- •4.8.5 Экспериментальные методы ядерной физики. Методы регистрации частиц
- •4.8.6 Физика элементарных частиц
- •4.8.7 Космические лучи. Мезоны и гипероны. Классификация элементарных частиц
- •Содержание
3.4 Магнитное поле
3.4.1 Магнитное поле. Закон Ампера. Взаимодействие параллельных токов
Взаимодействие токов осуществляется через поле, называемое магнитным. Это название связано с опытами, которые проводил в 1820 г. Эрстед, и где обнаружил, что поле, возбуждаемое током, оказывает ориентирующее действие на магнитную стрелку. При включении тока стрелка устанавливалась перпендикулярно к проволоке. Изменение направления тока заставляло стрелку повернуться в противоположную сторону. Из опытов Эрстеда следует, что магнитное поле имеет направленный характер и должно характеризоваться векторной величиной. Эту характеристику магнитного поля назвали магнитной индукцией и обозначили буквой В.
Магнитное поле, в отличие от электрического, не оказывает действия на покоящийся заряд. Сила возникает лишь тогда, когда заряд движется. Проводник с током представляет собой электрически нейтральную систему зарядов, в которой заряды одного знака движутся в одну сторону, а заряды другого знака движутся в противоположную сторону. Отсюда следует, что магнитное поле порождается движущимися зарядами.
Итак, движущиеся заряды (токи) изменяют свойства окружающего их пространства — создают в нем магнитное поле. Таким образом, источником магнитного поля всегда является электрический ток. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы со стороны электрического поля. Этим объясняется действие магнитного поля на рамку с током: вращающий момент, испытываемый рамкой, есть результат действия сил поля на ее отдельные элементы.
Изучая, как проводники различной формы, по которым протекает ток, взаимодействуют между собой, Ампер установил, что это взаимодействие может рассматриваться как совокупность взаимодействий сколь угодно малых участков этих проводников с током - элементов тока.
Элементом тока называют векторную величину Idl, равную произведению силы тока I в проводнике на длину dl данного участка проводника. Направление элемента тока совпадает с направлением тока на этом участке проводника. Обобщая результаты исследования, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника Idl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:
|
dF = I[dl, В] |
(3.87). |
Модуль силы Ампера вычисляется по формуле
|
dFА = IBdlsinα |
(3.88), |
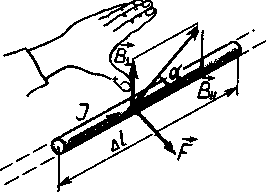
где α — угол между векторами dl и В. Силу, действующую на проводник с током (или элемент тока) в магнитном поле, называют силой Ампера.. Направление вектора dF может быть найдено по общим правилам векторного произведения, или по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на проводник с током (рисунок - 3.24).
Если магнитное поле является однородным и проводник длиной l целиком находится в нем, то формула силы Ампера принимает вид
|
FА = IBlsinα. |
(3.89). |
Отсюда найдем индукцию магнитного поля.
|
B = FА/IBlsinα. |
(3.90). |
Это выражение раскрывает физический смысл B индукции магнитного поля, как силы, которая действует на элемент длины проводника с током I, помещенного в магнитное поле.
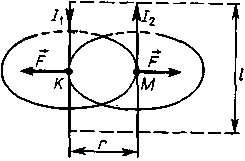
Закон Ампера позволяет определить силы взаимодействия двух параллельных токов. Опыт показывает, что электрические токи взаимодействуют между собой. Например, два тонких прямолинейных параллельных проводника, по которым текут токи притягиваются друг к другу, если токи в них имеют одинаковое направление, и отталкиваются, если токи противоположны (рисунок - 3.25).
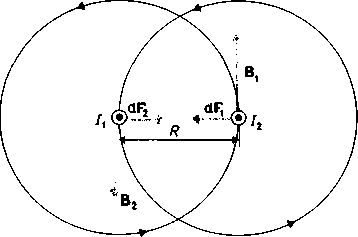
Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2 (направления токов указаны на рисунке - 3.26), расстояние между которыми равно R. Каждый из проводников создает магнитное
|
|
|
|
|
Рисунок - 3.24 |
Рисунок - 3.25 | |
поле, которое действует по закону Ампера на другой проводник с током. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности.
|
|
|
Рисунок - 3.26 |
Направление вектора B1 задается правилом правого винта, его модуль равен:
|
B = (μ0 μ/4π) 2I1/R |
(3.91). |
Магнитное поле тока I1, действует на элемент dl второго проводника с током I2 с силой: dFl=I2B1dl. Подставляя значение для B1, получим dFl= (μ0 μ/4π) 2I1 I2 dl/R.
Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна dF2= I1B2dl = (μ0 μ/4π) 2I1 I2 dl/R. Сравнение выражений для dF1 и dF2 показывает, что они одинаковы, т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
|
dF= (μ0 μ/4π) 2I1 I2 dl/R |
(3.92). |
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой той же формулой.
Опыты показывают, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: индукция магнитного поля В, порождаемое несколькими токами, равно векторной сумме полей Вi, порождаемых каждым током в отдельности:
|
В =∑Вi |
(3.93). |
Для графического изображения магнитных полей и определения направления вектора магнитной индукции вводится представление о линиях магнитной индукции. Линиями магнитной индукции называются кривые, касательные к которым в каждой точке совпадают с направлением вектора В в этих точках поля. Линии магнитной индукции всегда замкнуты и охватывают проводники с токами, которые их создают. Замкнутость линий индукций является выражением отсутствия в природе свободных магнитных зарядов. Магнитное поле называется однородным, если векторы В во всех его точках одинаковы. В противном случае ноле является неоднородным.
Направление линий индукции магнитного поля тока определяется правилом Максвелла (правилом буравчика): если ввинчивать буравчик по направлению тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции (рисунок - 3.27).
С помощью потока линий магнитной индукции ФВ графически удобно выразить величину магнитного поля в той или иной точке пространства.
Магнитной цепью называется совокупность тел или областей пространства, в которых сосредоточено магнитное поле. Магнитные цепи составляют необходимую часть электрических машин и многих электрических устройств.
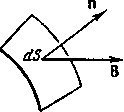
Магнитный поток в магнитной цепи играет роль, аналогичную силе тока в электрической цепи. Во всех сечениях неразветвленной магнитной цепи магнитный поток Фт должен быть одинаковым. Элементарный поток dФВ вектора магнитной индукции В сквозь участок поверхности с площадью dS (рисунок - 3.28):
|
dФВ = В dS cos (В, n) — BndS = B dSn |
(3.94), |
где n — единичный вектор внешней нормали к площадке dS, Bn — проекция вектора В на направление нормали.
|
|
|
|
Рисунок - 3.27 |
Рисунок - 3.28 |
Магнитный поток Фт сквозь произвольную поверхность S находится суммированием или интегрированием всех элементарных потоков:
|
Фт =∫BdS cos В,n) = ∫ Вп dS = \B dS |
(3.95). |
Для однородного поля и плоской поверхности S, расположенной перпендикулярно к вектору В: Вп = В = const, Фт = BS.
Теорема Остроградского—Гаусса применительно к магнитному полю утверждает: магнитный поток сквозь произвольную замкнутую поверхность равен нулю:
|
∫Вп dS = 0 |
(3.96). |
Теорема выражает отсутствие в природе магнитных зарядов и замкнутость линий индукции магнитного поля.