3.2 Электрическое поле в диэлектриках
3.2.1 Электроемкость проводников, конденсаторы
Опытом установлено, чем больше заряд, сообщаемый проводнику, тем больше его потенциал, т.е. заряд проводника пропорционален его потенциалу q = CU. Постоянная. С есть величина, характерная для каждого проводника при данных внешних условиях и называемая его электрической емкостью:
|
C = q/U |
(3.30). |
Численно емкость равна количеству электричества, на которое нужно изменить заряд проводника, чтобы его потенциал изменился на единицу. Если форма и размеры проводника не меняются и если при этом остаются неизменными внешние условия (не изменяется среда, в которой находится проводник, не изменяется расположение окружающих предметов), то и емкость остается величиной постоянной. Это показывает, что емкость зависит от формы и размеров, но не зависит от материала проводника.
Из электростатики мы установили, что потенциал уединенного шара радиуса R в среде с диэлектрической проницаемостью ε, равен
|
φ = q/4πε0εR |
(3.31). |
Сравнивая с формулой, определяющей емкость, находим, что емкость шара равна
|
С = 4πε0εR. |
(3.32) |
Таким образом, емкость уединенного проводящего шара пропорционален его радиусу. Расчеты по полученной формуле показывают, что емкостью 1 Фарад должен обладать шар радиусом R = С/4πε0ε ≈ 9*106 км, что примерно в 1400 раз больше радиуса Земли. Следовательно Фарад, очень крупная единица измерения. Поэтому в обычной жизни допускается оперирование долями Фарад – пикофарад (10-12 Ф), нанофарад (10-9 Ф) и т.д.
В различных электротехнических и радиотехнических устройствах часто необходимы значительные электроемкости, которые образуются из системы проводников. Система проводников, предназначенных для образования значительной емкости, называется конденсатором, а сближенные проводники, образующие конденсатор, называются обкладками конденсатора.
Под емкостью С конденсатора подразумевают величину отношения заряда q одного знака, накопленного в конденсаторе к разности потенциалов ∆φ между обкладками:
|
C = q/∆φ |
(3.33). |
Эта величина, как и емкость уединенного проводника, зависит лишь от геометрических факторов и величины диэлектрической постоянной изолирующей прослойки между обкладками конденсатора. Исследуем емкости таких конденсаторов.
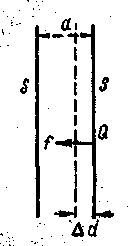
Плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин (рисунок 3.13,а), расположенных друг от друга на расстоянии d, малом по сравнению с их собственными размерами. Пространство между пластинами конденсатора заполнено диэлектриком. По определению емкость конденсатора C = q/∆φ .
Выразим емкость плоского конденсатора через величины, характеризующие его размеры. Так как размеры пластин велики по сравнению с расстоянием между ними, то ∆φ поля между пластинами такая же, как и в случае двух бесконечных плоскостей, несущих равные по численному значению заряды противоположных знаков.
Если σ — поверхностная плотность зарядов на этих пластинах, a S — площадь одной пластины конденсатора, то заряд конденсатора q = σS,. При наличии диэлектрика между обкладками разность потенциалов между ними можно рассчитать как для системы двух заряженных пластин:
|
∆φ = σd/ε0ε |
(3.34). |
Подставим в формулу емкости и получим выражение емкости плоского конденсатора:
|
C = q/∆φ = σS/ σd/ε0ε = ε0ε S/d |
(3.35). |
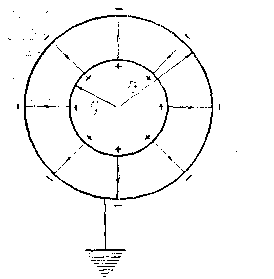
Сферический конденсатор. Сферический конденсатор состоит из двух концентрических шаровых обкладок, разделенных сферическим слоем диэлектрика. Если внутренней обкладке такого конденсатора сообщить заряд +q, то на внешней заземленной обкладке образуется наведенный заряд -q ((рисунок – 3.13,б).).
Поле сферического конденсатора сосредоточено между его обкладками и таково, как если бы заряд был сосредоточен в центре сферы. Поэтому потенциалы обкладок равны: φ1 = q/εr1, φ2 = q/εr2. Поэтому разность потенциалов между обкладками конденсатора равен φ1 – φ2 = q/ε(1/r1 - 1/r2) = q (r1 - r2)/ εr1r2. что позволяет найти электроемкость сферического конденсатора
|
C = q/∆φ = εr1r2 /(r1 - r2) |
(3.36). |
Если d = (r2 — r1)« r1 то r 2≈ r1≈ r и C = εr2/ d. Умножая числитель и знаменатель на 4π, и отмечая, что 4πr2 есть площадь поверхности сферической обкладки, получим
|
C = εS/4πd |
(3.37). |
Таким образом, при малой величине зазора по сравнению с радиусом сферы выражение для емкости сферического и плоского конденсатора совпадают. Если внешний радиус сферического конденсатора гораздо больше внутреннего радиуса, то формула (3.37) упрощается:
|
C = εr1 |
(3.38), |
т.е., в этом она равна емкости уединенного шара радиуса r1.
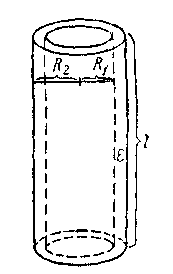
Цилиндрический конденсатор. Цилиндрический конденсатор состоит из двух цилиндрических обкладок, имеющих общую ось и разделенных цилиндрическим слоем диэлектрика (рисунок 3.13,в).
|
|
|
|
|
а) |
б) |
в) |
|
Рисунок - 3.13 | ||
Если внутреннюю обкладку такого конденсатора зарядить (при внешней заземленной обкладке), то, пренебрегая краевыми эффектами, его поле можно считать радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Напряженность поля между обкладками конденсатора создается только зарядом на внутреннем цилиндре и в точке на расстоянии r от оси цилиндра равна: Е = 2τ/εr, где τ - линейная плотность зарядов. Изменение потенциала на участке dr связано соотношением: - dφ/dr = E, откуда dφ = -E dr = -( 2τ/εr) dr. Разность потенциалов между обкладками (φ2 – φ1) получим, интегрируя это выражение в пределах от R1 до R2: φ2 – φ1 = - ∫( 2τ/εr) dr = - 2τ/εr ln(R2/R1). Следовательно, емкость цилиндрического конденсатора
|
С = q/(φ1 – φ2) = εl/2ln(R2/R1) |
(3.39), |
где R2 и R1 — радиусы цилиндров.
Емкость подземных и одножильных кабелей может вычисляться по формуле цилиндрического конденсатора, при этом роль внутренней обкладки играет металлическая жила, роль внешней обкладки — броня.
Величину емкости можно менять, соединяя конденсаторы в батареи различным образом.
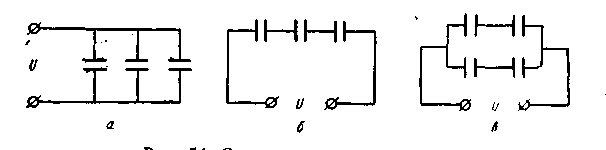
При параллельном соединении конденсаторов (рисунок - 3.14, а) общим для всех конденсаторов является напряжение U, поэтому U = U1 = U2 = U3 ; Суммарный заряд батареи равен q = q1+q2+q3+ . Поэтому емкость батареи равна С =q/U = q1/U+q2/U+q3/U + . Но q1/U = С1, q2/U = С2, q3/U = С3 и т.д. Так что
|
С= С1+С2+ С3+ = ∑Ci, |
(3.40), |
т.е. емкость батареи при параллельном соединении конденсаторов равна сумме емкостей отдельных конденсаторов. Очевидно, в этом случае допустимое рабочее напряжение определяется соответствующим напряжением одного конденсатора.
При последовательном соединении конденсаторов (рисунок - 3.14, б) одинаковым для всех конденсаторов, благодаря явлению индукции, будет заряд q, равный полному заряду батареи: q = q1=q2=q3= . Напряжение же батареи определяется суммой напряжений на отдельных конденсаторах: U = = U1 + U2 + U3+ ; Поэтому для всей батареи справедливо: q/C = q /С1+ q /C2+ q/C3+ или
|
1/C = 1 /С1+ 1 /C2+ 1/C3+ = ∑1/Ci. |
(3.41). |
При последовательном соединении конденсаторов суммируются обратные величины емкостей. Т. е. при последовательном соединении п одинаковых конденсаторов емкость батареи в п раз меньше емкости одного конденсатора, во столько же раз напряжение на каждом конденсаторе меньше напряжения батареи.
Комбинируя оба типа соединений, можно получить смешанные батареи с разнообразными данными (рисунок - 3.14, в).
|
|
|
Рисунок - 3.14 |
Для расчета емкости при таком соединении можно сначала подсчитать емкость отдельных групп конденсаторов, представляющих батареи с параллельным или последовательным соединением, а затем каждую из них мысленно заменить одним конденсатором соответственной емкости.