3.1.4 Потенциал электростатического поля. Работа и энергия заряда в электрическом поле

Электрическое поле неподвижных зарядов называют также электростатическим, Поэтому энергия электростатического поля в той или иной точке зависит от положения точки и является потенциальной энергией.

Пусть пробный электрический заряд q₀ находится в электростатическом поле. Такой заряд под действием сил поля может прийти в движение. При перемещении этого заряда полем совершается работа. Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд q₀ в начальной и конечной точках своего перемещения в поле заряда q: A = (1/4πε₀) (q₀q)/ εr₁ - (1/4πε₀) (q₀q)/ εr₂ = Eп₁ – Еп₂, откуда следует, что потенциальная энергия заряда q в поле заряда q₀ равна E_п = q₀q /4πε₀ εr + C. Она определяется не однозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r→∞) потенциальная энергия обращается в нуль (E_п = 0), то С = 0 и потенциальная энергия заряда q, находящегося в поле заряда Q на расстоянии r от него, равна

Eп = q q0/4πε0 εr.

(3.17).

Для одноименных зарядов q₀q>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов q₀q <0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой п точечных зарядов q₁, q₂, , q_n, то работа электростатических сил, совершаемая над зарядом q₀, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия E_п заряда q₀, находящегося в этом поле, равна сумме его потенциальных энергий E_пi, создаваемых каждым из зарядов в отдельности: E_п = ∑ E_пi = q₀∑q_i/4πε₀ εr_i. Из этой формулы вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей этих зарядов:

φ = ∑ φi =∑qi/4πε0 εri.

(3.18).

Пусть заряд q в данной точке поля обладает потенциальной энергией Е_п. В различных точках поля потенциальная энергия данного заряда может быть различна, она зависит как от свойств поля, так и от величины заряда. Но если в одну и ту же точку поля помещать разные заряды потенциальная энергия которых соответственно равна Е_п1, Е_п2;.. .; Е_пi и взять отношение Е_п к q, то получается постоянная величина, не зависящая от величины заряда. Это отношение взято в качестве энергетической характеристики поля и называется потенциалом поля. Следовательно, потенциал данной точки поля определяется формулой

φ = Еп/q

(3.19).

Итак, потенциал φ какой-либо точки электростатического поля равен потенциальной энергии: приходящейся на единицу пробного заряда, помещенного в эту точку. Следовательно, потенциал поля есть величина, равная отношению потенциальной энергии заряда к величине заряда, помещенного в данную точку электростатического поля. Если напряженность поля есть силовая характеристика и является вектором, то потенциал— энергетическая характеристика поля и величина скалярная.

Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из полученной формулы следует, что потенциал поля, создаваемого точечным зарядом q, равен

φ = q/4πε0 εr

(3.20)

Система из двух точечных зарядов +q_x и -q₂, находящихся па расстоянии b друг от друга, называется диполем. Такую систему в физике рассматривают потому, что центры положительных и отрицательных зарядов молекул многих веществ можно представить смещенными друг относительно друга. Представление о диполях часто позволяет с известным приближением описать взаимодействие молекул различных веществ. Модель дипольного строения вещества лежит в основе теории диэлектриков.

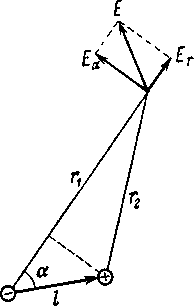
Величину произведения плеча на значение одного из зарядов, образующих диполь, называют электрическим моментом диполя: p = qb. Электрический момент представляет собой вектор, длина которого изображает величину момента, а направление совпадает с осью диполя от отрицательного заряда к положительному заряду. Пользуясь рисунком- 3.10, произведем расчет поля диполя. По принципу суперпозиции, потенциал поля диполя в точке наблюдения равен

φ = q/4πε0 ε (1/r2 -1/r1) =( q/4πε0 ε)* (r1-r2)/r2* r1

(3.21)

где r₂ и r₁ — расстояния от положительного и отрицательного зарядов диполя до точки наблюдения. Пусть точка наблюдения выбрана так, что длина b«r намного меньше расстояний r₂ и r₁. В этом случае можно положить, что r₁ - r₂≈ bcosα; r_2* r₁ ≈ r², и предыдущую формулу можно переписать так: φ = qbcosα/ r²=p cosα/ r², где α— угол между направлением момента диполя и направлением к точке наблюдения, проведенным из диполя. Зная зависимость φ(r,) можно определить напряженность поля по соответствующим формулам.

Рисунок - 3.10

Чтобы определить величину напряженности поля Е в той же точке, найдем сначала величины составляющих напряженности поля в направлении радиуса Е_r и перпендикулярно к нему Е_α (рисунок - 3.10).

Е = √ Е2r+ Еα2

(3.22).

Величины же составляющих легко найдутся по формуле, выражающей связь между напряженностью и потенциалом поля:

Еr = - dφ/db

(3.23).

Применяя эту формулу к вычислению Е_r находим, что db = dr, α = const, и, cледовательно, Е_r = - d/dr(p cosα/ r²) = 2p cosα / r².

При вычислении Е_α, учтем, что при перемещении на величину db, в направлении, перпендикулярном к радиусу, r = const, а угол α изменится на величину db =r dα.

Тогда Е_α = - dφ/dl =- 1/r (dφ/dα) = - 1/r [d(p cosα)/r²]dα = 2p sinα / r², и далее, Е = √ Е²_r+ Е_α² = p/r²√ 4cos²α + sin²α = p/r²√ 3cos²α + 1.

На одинаковом расстоянии от центра диполя наибольшее значение напряженности поля будет на оси диполя, когда cos²α =1, а наименьшее — в направлении, перпендикулярном к оси, когда cos² α = 0. Следовательно,

Emax = 2p/r2, Emin = p/r2 = Emax /2

(3.24).

Нетрудно увидеть, что ось диполя является осью симметрии поля. Напряженность и потенциал поля диполя убывают обратно пропорционально целым степеням расстояния, причем показатели степени оказываются большими на единицу, чем для соответствующих величин точечного заряда.

Работа, совершаемая силами электростатического поля при перемещении заряда q из точки 1 в точку 2, может быть представлена какA₁₂ = - q ∆ Е, или

A = q (φ2 — φ1).

(3.25).

Как видно, работа, совершаемая электростатическими силами при перемещении электрического заряда из одной точки электрического поля в другую, равна произведению величины электрического заряда на разность потенциалов в этих точках поля. Полученная формула есть одно из основных соотношений электростатики, из которого следует, что работа электростатического поля по перемещению заряда между двумя точками не зависит от формы пути, а является функциями положения начальных и конечных точек перемещения. Физический смысл имеет понятие разность потенциалов, но считается, что электрическое поле в бесконечности имеет нулевой потенциал φ_∞ = 0. Поэтому, когда говорят о потенциале точки, условно принимается за уровень отсчета потенциал бесконечно удаленной точки с φ_∞=0. Этим свойством электростатического поля пользуются при рассмотрении многих задач электростатики, например, при определении потенциала точечного заряда.

Пусть работа поля при бесконечно малом перемещении dr = dl cosα равна dA, тогда для вычисления работы электрических сил на конечном пути l необходимо взять интеграл вида А = ∫dA. Элементарная работа электрических сил при бесконечно малом перемещении dr заряда q (рисунок - 3.11) равна

dA = Eqdl cos α,

(3.26),

где α—угол между напряженностью поля и направлением элементарного смещения. Величина Ecos α = Е_l, есть проекция

Рисунок - 3.11

напряженности поля на направление dl. Таким образом, dA = qE_l dl. Если электрический заряд перемещается по произвольному замкнутому контуру так, что начало пути, совпадает с его концом, то результирующая работа электрических сил равна нулю (разность потенциалов равна нулю): А=0.Поэтому для замкнутого контура q ∫ E_ldl = 0;так как q≠0, то

∫Eldl = 0

(3.27).

Величина ∫E_ldl называется циркуляцией вектора напряженности поля. Таким образом, циркуляция вектора напряженности электростатического поля по произвольному контуру равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным, а силы поля – консервативным.

Если в одну точку пространства приходят электрические поля из разных источников, то вследствие свойства суперпозиции электрических полей результирующий потенциал φ в данной точке будет равен алгебраической сумме потенциалов φ₁,φ₂ , ,φ_n. создаваемых отдельными зарядами:

φ = φ1+φ2 + +φn = ∑φi

(3.28).

В электрическом поле можно сформировать поверхность так, чтобы все ее точки имели бы один и тот же потенциал. Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями.

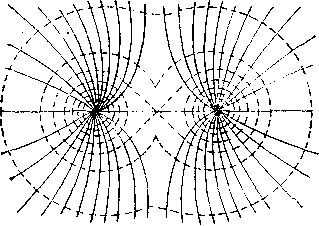
Пользуясь эквипотенциальными поверхностями, можно электрические поля изобразить графически, подобно тому, как это делается с помощью силовых линий. Так как все точки эквипотенциальной поверхности имеют одинаковый потенциал, то работа перемещения заряда вдоль поверхности равна нулю. Это значит, что электрические силы, действующие на заряд, всегда направлены по нормалям к поверхности равного потенциала. Отсюда следует, что силовые линии всегда перпендикулярны к эквипотенциальным поверхностям. На рисунке - 3.12 изображены эквипотенциальные поверхности и силовые линии: а) - точечного заряда, б) – двух одноименных зарядов, в) – эквипотенциальные линии электрического поля тела произвольной формы.

а)	б)	в)
Рисунок - 3.12

Эквипотенциальные линии на графике можно проводить с произвольной густотой, но обычно их проводят на картах полей так, чтобы они соответствовали одинаковым приращениям потенциала, например 1, 2, 3 и т. д. вольт. В этом случае быстрота изменений потенциала в направлении силовых линий будет обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. Поэтому густота эквипотенциальных линий пропорциональна напряженности поля. Таким образом, по картине расположения эквипотенциальных поверхностей и расположении силовых линий. всегда можно составить представление об электрическом поле.

Установим теперь соотношение между потенциалом и напряженностью. Существование такой связи следует из того факта, что работа электрических сил, выражаемых через напряженность, вместе с тем выражается и через разность потенциалов точек поля. Как явствует из предыдущего, электрическое поле может быть охарактеризовано различными величинами:— векторной величиной—напряженностью и скалярной величиной—потенциалом. Установим связь между этими характеристиками поля. Искомую связь получим, сравнивая выражения работы через напряженность и через потенциал поля: dA = qEdl и dA = —dЕ = —qdφ. Приравнивая оба выражения для работы и сокращая на q, получим: E dl = —dφ. Отсюда

E = — dφ/dl = -gradφ

(3.29).

Эту мысль выражают следующим образом: напряженность поля равна градиенту потенциала, взятому с обратным знаком. Знак минус означает, что потенциал убывает при перемещении в направлении силовой линии, и, таким образом, напряженность поля измеряется изменением потенциала, приходящимся на единицу длины в направлении силовой линии, т. е. в направлении наиболее значительного уменьшения потенциала. Из формулы связи между потенциалом и напряженностью электростатического поля определяется единица измерения напряженности в СИ: В/м.