1.3 Динамика вращательного движения твердых тел

1.3.1 Момент силы, момент импульса. Закон сохранения момента импульса

В механике твердым телом называется совокупность материальных частиц, взаимное расположение которых остается неизменным. Основные законы механики определяют движение отдельной материальной точки.

При вращательном движении угловая скорость и угловое ускорение одинаковы в каждый данный момент для всех частиц тела. В связи с неизменностью взаимного расположения частиц линейные скорости и линейные ускорения пропорциональны расстоянию частиц от оси вращения. Этим определяется та исключительная роль, которую играет расстояние частиц от оси вращения в динамике вращательных движений твердого тела.

Если на твердое тело, имеющее закрепленную ось вращения, действует сила F, приложенная в точке А (рис. 54), то очевидно, что составляющая F₁ этой силы, параллельная оси вращения, никакого вращательного эффекта дать не может, и только другая составляющая, лежащая в плоскости, перпендикулярной к оси вращения, F₂, дает вращательный эффект, который тем более значителен, чем больше кратчайшее расстояние между прямой, по которой действует сила, и осью вращения.

Поэтому моментом силы относительно оси называют произведение проекции силы (на плоскость, перпендикулярную к оси) и кратчайшего расстояния между прямой, по которой действует сила, и осью. Момент силы относительно оси рассматривают как вектор, направленный по оси туда, куда нужно смотреть, чтобы видеть силу обращенной в сторону движения часовой стрелки (т. е. на рисунке - 1.33 вниз). Момент силы F относительно оси численно равен М = F₂p.

Рисунок - 1.33

Твердое тело можно мысленно представить в виде системы материальных точек — достаточно малых частей этих тел. Рассмотрим произвольную механическую систему, состоящую из п материальных точек. Пусть m_i— масса i-й точки системы, а r_i— радиус-вектор, проведенный в эту точку из начала координат О неподвижной инерциальной системы отсчета.

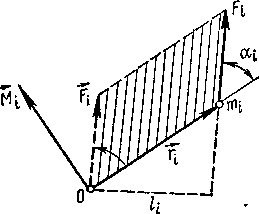
Векторное произведение радиуса-вектора r_i, проведенного в точку приложения силы F_i на' эту силу называют моментом М силы, F_i относительно точки О:

Мi = [ri Fi]

(1.117).

Векторы М_i , r_i и F_i образуют правую тройку (рисунок - 1.34). Численное значение момента силы F; равно

Мi = Fi risinα = Fili

(1.118,

где α-— угол между векторами r_i и F_i, r_isinα = l_i— длина перпендикуляра, опущенного из точки О на линию действия силы F_t. Величина l_t называется плечом силы F_i. Если линия действия силы проходит через точку О, то l_t = 0 и момент силы относительно точки О тоже равен нулю.

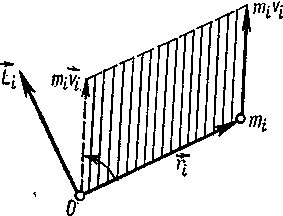
Векторное произведение радиуса-вектора r_i на ее импульс mv, называют моментом импульса L_i относительно точки О:

Li = [rimivi]

(1.119).

Он направлен перпендикулярно к плоскости, проведенной через векторы r_i и m_iv_i и образует с ними правую тройку векторов: при наблюдении из конца L_i видно, что кратчайший поворот от r_i к m_iv_i происходит против часовой стрелки (рисунок - 1.35). Из полученных соотношений следует, что скорость изменения момента импульса L_i i-ой материальной точки равна

dL/dt = ∑Mik + Miвнешн

(1.120).

Сложим почленно все уравнения, записанные для каждой из n материальных точек системы: ∑dL_i/dt =∑ ∑M_ik + ∑Mi^внешн. Векторную сумму моментов Mi^внешн всех внешних сил, приложенных ко всем материальным точкам системы, называют результирующим, или главным моментом М внешних сил относительно точки О: М = ∑Mi^внешн

Рисунок - 1.34	Рисунок - 1.35

Векторную сумму моментов импульса L_i, всех материальных точек системы называют моментом импульса (количества движения) L тела относительно точки О:

L = ∑Li =∑[ri,mivi]

(1.121).

Для тела выполняется соотношение:

dL/dt =∑dLi/dt

(1.122).

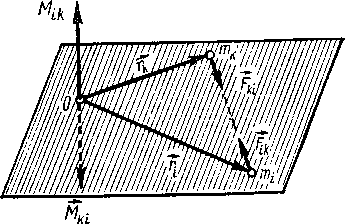
Наконец, векторная сумма моментов всех внутренних сил F_lk взаимодействия между всеми точками системы относительно точки 0 равна нулю: ∑ ∑M_ik = 0. Это связано с тем, что по третьему закону Ньютона силы F _iк и F_kt численно равны, имеют общую линию действия, но направлены во взаимно противоположные стороны. Поэтому их моменты M_ik = [r_i, F_ik] и M_ki = [r_k,, F_ki] относительно точки О, численно равны и противоположны по направлению (рисунок - 1.36).

Рисунок - 1.36

Поэтому

∑dL/dt = M

(1.123).

Таким образом, скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. Это утверждение выражает основной закон динамики для тела, вращающегося вокруг неподвижной точки. Отсюда следует, что момент импульса L является основной динамической характеристикой тела, вращающегося вокруг неподвижной точки.

Из основного закона динамики для тела, вращающегося вокруг неподвижной оси, следует закон сохранения момента импульса тела относительно этой оси: если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется. Действительно для случая, когда на тело либо вовсе не действуют внешние силы, либо они таковы, что их равнодействующая не дает момента относительно оси вращения. Тогда dL = M dt = 0. Но если dL равно нулю, то, следовательно, сама величина момента импульса L = остается постоянной: L = const. Этот утверждение и носит название закона сохранения момента импульса относительно оси вращения.

Закон сохранения момента импульса, подобно законам сохранения импульса и энергии, является одним из фундаментальных законов природы. В теоретической физике доказано, что этот закон — следствие изотропности пространства. Изотропность пространства означает, что при повороте в нем замкнутой системы как целого (иначе говоря, при изменении ориентации осей координат) физические свойства замкнутой системы и законы ее движения не изменяются.