
- •Аннотация
- •Условия использования
- •Оглавление
- •Содержание
- •Только для взрослых
- •Десять лет спустя
- •Чему нас учат семья и школа?
- •Крошка сын к отцу пришел
- •Азбучные истины
- •Что я могу ещё сказать?
- •Благодарности
- •Детям до 16-ти
- •Глава 1 Путь далек у нас с тобою…
- •Компьютер
- •Компилятор
- •Личный багаж
- •Компьютерная литература
- •В здоровом теле – здоровый дух
- •Вместе весело шагать по просторам!
- •Повторение – мать учения
- •Соглашения
- •Итоги
- •Глава 2 Вместо теории
- •Миф о думающих машинах
- •Загадочные коды
- •Языки программирования и компиляторы
- •Следующий шаг –
- •Итоги
- •Глава 3 Консольный интерфейс
- •Что такое интерфейс?
- •Консольный интерфейс
- •Прикосновение к консольному интерфейсу
- •А почему не «окна»?
- •Итоги
- •Глава 4 Оружие – к бою!
- •Оружейный прилавок
- •Free Pascal
- •Настройка ярлыка
- •Free Pascal
- •Установка справочной системы
- •Обновление версий Free Pascal
- •Итоги
- •Глава 5 Программа номер один
- •Постановка задачи
- •Создание файла
- •Наполнение файла
- •Компиляция
- •Процедура вывода (печати)
- •Запуск программы
- •Итоги
- •Глава 6 Подготовка к следующему штурму
- •Ещё об исходных файлах
- •Управление окном редактора
- •Борьба с ошибками
- •Итоги
- •Глава 7 Развиваем успех
- •Операторы и разделители
- •Программа, стой!
- •Алгоритмы
- •Блок-схемы
- •Итоги
- •Глава 8 Постоянные и переменные
- •Константы
- •Идентификаторы
- •Переменные
- •Ввод и вывод данных
- •Итоги
- •А слабо?
- •Глава 9 Переменные: продолжение знакомства
- •Представьтесь, пожалуйста!
- •Из пустого в порожнее
- •Сцепление строк
- •Инициализация переменных
- •Типизированные константы
- •Итоги
- •А слабо?
- •Глава 10 Условный оператор
- •Стой! Кто идет?
- •Вопрос ребром
- •Пост номер один
- •Неполный условный оператор
- •Пост номер два
- •Итоги
- •А слабо?
- •Глава 11 Операторный блок
- •Операторные скобки
- •Красиво жить не запретишь
- •Комментарии
- •Итоги
- •Глава 12 Цикл с проверкой в конце
- •Подтянем дисциплину
- •Нанимаем репетитора
- •Вежливый часовой
- •Досрочный выход из цикла
- •Итоги
- •Глава 13 Правда и кривда
- •Есть ли жизнь на Марсе?
- •Информация и её мерило
- •Булевы переменные
- •Ввод и вывод булевых данных
- •Логические выражения
- •С высоты птичьего полета
- •Парад логических операций
- •Итоги
- •А слабо?
- •Глава 14 Дважды два – четыре
- •Поможем братьям нашим меньшим
- •Числа и действия с ними
- •Алгоритм экзаменатора
- •Экзаменатор, первый вариант
- •Итоги
- •А слабо?
- •Глава 15 Айда в Монте-Карло!
- •Куда ни глянь – то процедура, то функция!
- •Госпожа удача
- •Итоги
- •А слабо?
- •Глава 16 Делу время, а потехе час
- •Потемкинская лестница
- •Итоги
- •А слабо?
- •Глава 17 И вновь за парту
- •Цикл со счетчиком
- •Итоги
- •Глава 18 Аз, Буки
- •Символьный тип данных
- •Индексация
- •Длина строки
- •Распечатка строки
- •Итоги
- •Глава 19 Процедуры и функции: разделяй и властвуй
- •Снежный ком
- •Описание процедур
- •Процедуры с параметрами
- •Итоги
- •Глава 20 Процедуры: первый опыт
- •Мухи – налево, котлеты – направо!
- •Сверху вниз
- •Первые раны
- •Глобальные и локальные
- •Локально – это разумно!
- •Неподдающаяся строка
- •Итоги
- •Глава 21 Отладка
- •Отладчик
- •Жучки, вылезайте!
- •Ссылка на переменную
- •Итоги
- •Глава 22 О передаче параметров
- •Процедура обмена
- •Замена символов в строке
- •О передаче строк
- •Итоги
- •Глава 23 Функции
- •Объявление функции
- •Пример функции
- •Подсчет символов в строке
- •Возврат строк
- •Когда результат не важен
- •Неявная переменная Result
- •Итоги
- •Глава 24 Криптография
- •Секреты Юлия Цезаря
- •Суть проблемы
- •О кодировании символов
- •Чудесные превращения
- •Шифрование символа
- •Расшифровка символа
- •Итоги
- •А слабо?
- •Глава 25 Текстовые файлы
- •Файлы хорошие и разные
- •Формат текстовых файлов
- •Доступ к текстовым файлам
- •Чтение из файла
- •Последовательный доступ к файлу
- •Самореклама
- •Цикл с проверкой в начале
- •Итоги
- •Глава 26 Я не читатель, — я писатель!
- •Запись в текстовый файл
- •Пример записи в файл
- •Завершение шпионского проекта
- •Итоги
- •А слабо?
- •Глава 27 Дайте кораблю минутный отдых!
- •Ошибка ошибке рознь
- •Фатальные ошибки
- •«Простительные» ошибки
- •Опции компилятора
- •Обработка ошибок ввода-вывода
- •Директивы компилятора
- •Директиву – в студию!
- •Парад директив
- •Итоги
- •А слабо?
- •Глава 28 Редактор и справочная система
- •Небьющиеся окна
- •Буфер обмена
- •Справочная система
- •Итоги
- •Глава 29 Читайте по-новому
- •Полицейская база данных, версия 1
- •Полицейская база данных, версия 2
- •Итоги
- •Глава 30 Журнальная история
- •Статистика знает всё?
- •Строим планы
- •Барабаним по клавишам
- •Первый блин
- •Блин второй
- •Спецификатор ширины поля
- •«Развесные» числа
- •Итоги
- •Глава 31 Финал журнальной истории
- •Буква за буквой
- •Нелишняя предосторожность
- •Достройка программы
- •Испытание
- •Итоги
- •Глава 32 Порядковые типы данных
- •Типы данных: простые и сложные
- •Целое братство
- •Капля, переполняющая чашу
- •Инкремент и декремент
- •Диапазоны
- •Перечисления
- •Порядковые типы
- •Разумный контроль
- •Итоги
- •Глава 33 Вещественные числа
- •Изображение вещественных чисел
- •Вывод вещественных чисел
- •Типы вещественных чисел
- •Сравнение вещественных чисел
- •Типы данных пользователя
- •Совместимость и преобразование типов
- •Размеры переменных и типов данных
- •Итоги
- •Глава 34 Структура программы
- •Управляющие структуры
- •Структура программы
- •Структура процедур и функций
- •Обмен данными с подпрограммами
- •Встроенные процедуры и функции
- •Что дальше?
- •Итоги
- •А слабо?
- •Глава 35 Множества
- •В директорском кабинете
- •Первым делом, первым делом – оцифровка
- •Множества глазами математика
- •Числовые множества
- •Мощность множества, полные и неполные множества
- •Итоги
- •Глава 36 Множества в Паскале
- •Объявление множеств
- •Присвоение значений множествам
- •Операции с множествами
- •Сравнение множеств
- •Проверка на вхождение элемента в множество (операция IN)
- •Решение директорской задачи
- •Итоги
- •А слабо?
- •Глава 37 Ввод и вывод множеств
- •Вывод множества в текстовый файл
- •Ввод множества из текстового файла.
- •Директорская задача, первый вариант
- •Директорская задача, второй вариант
- •Итоги
- •Глава 38 Множества «в бою»
- •Активисты, шаг вперед!
- •Подвиг контрразведчика
- •В тридевятом царстве
- •Решето Эратосфена
- •Мелочь, а приятно
- •Итоги
- •А слабо?
- •Глава 39 Командная игра (массивы)
- •Снежная лавина
- •А где же волшебная палочка?
- •Массивы вокруг нас
- •Объявление массивов
- •Доступ к элементам (индексация)
- •Ввод и вывод массивов
- •Ошибки индексации
- •Итоги
- •Глава 40 Пристрелка на знакомых мишенях
- •Вопрос-ответ – добиваемся гибкости
- •Полицейская база данных – ускоряем поиск
- •Ещё раз о статистике
- •Итоги
- •Глава 41 По порядку, становись!
- •Пиратская справедливость
- •Пузырьковая сортировка
- •Электронная делёжка
- •Возвращение на футбольное поле
- •Итоги
- •Глава 42 Кто ищет, тот всегда найдет
- •Где эта улица, где этот дом?
- •Последовательный поиск
- •Двоичный поиск
- •Исследование двоичного поиска
- •Ах, время, время!
- •Логарифмы? Это просто!
- •Итоги
- •Глава 43 Сортировка по-взрослому
- •«Фермерская» сортировка
- •Быстрая сортировка
- •Процедура быстрой сортировки
- •О рекурсии и стеке
- •Алгоритмы, на старт!
- •Итоги
- •Глава 44 Строки
- •Строка – особый род массива
- •Укороченные строки
- •Операции со строками
- •Подсчет слов в строке
- •Контекстная замена
- •Итоги
- •Глава 45 Очереди и стеки
- •Вовочка в потоке событий
- •Танцевальный кружок
- •Скитания товарного вагона
- •Сортировочная горка
- •Итоги
- •Глава 46 Огромные числа
- •Сколько звезд на небе?
- •Сложение «в столбик» никто не отменял
- •Великая стройка
- •Длинная арифметика
- •Итоги
- •А слабо?
- •Глава 47 Системы счисления
- •Из тьмы веков
- •Число и его изображение
- •Десятичная система
- •Двоичная система
- •Шестнадцатеричная система
- •Другие системы счисления
- •Изображение числа в заданной системе счисления
- •Обратное преобразование
- •Итоги
- •Глава 48 Железная логика
- •Два взгляда на компьютерные «кирпичики»
- •Логические операции в регистрах
- •Сдвиги влево и вправо
- •Итоги
- •Глава 49 Сложные массивы
- •На поклон к Науке
- •Имперское строительство
- •Крестики-нолики
- •Итоги
- •А слабо?
- •Глава 50 Неспортивные рекорды (записи)
- •Кушать подано!
- •Записи
- •Второй тайм
- •Дополнительное время
- •Итоги
- •Глава 51 Указатели в море памяти
- •Погружение в оперативную память
- •«Планировка» памяти
- •Указатели, первое знакомство
- •Объявление указателей
- •Копирование указателей, пустой указатель
- •Сравнение и проверка указателей
- •Разыменование указателей
- •Нетипичный указатель
- •Примеры с указателями
- •Итоги
- •Глава 52 Динамические переменные
- •Аппетит является к обеду
- •Одолжите памяти немножко!
- •Выделение памяти
- •Освобождение памяти
- •Предупреждён – значит, вооружен
- •Итоги
- •Глава 53 Массив указателей
- •Базу данных – в кучу
- •Сортировка массива указателей
- •Итоги
- •А слабо?
- •Глава 54 Односвязные списки
- •Чудесное сочетание
- •Проблема курицы и яйца
- •Вяжем список
- •Распечатка списка
- •Поиск в несортированном списке
- •Сортированные списки
- •Поиск в сортированном списке
- •Итоги
- •Глава 55 Слова, слова, слова…
- •Частотный анализ текста
- •Слово за слово
- •Структура записи
- •Алгоритм
- •А слабо?
- •Глава 56 И снова очереди, и снова стеки…
- •Шутить изволите?
- •Танцуют все!
- •Итоги
- •Глава 57 Графомания
- •Видимое представление графа
- •Внутреннее представление графа
- •Ввод и вывод графа
- •Итоги
- •Глава 58 По графу шагом марш!
- •Империя номер два
- •Структура узла
- •В рассыпную!
- •Аты-баты
- •Итоги
- •Глава 59 Крупные проекты
- •О модулях и разделении труда
- •Модули
- •Дробление модуля – «смертельный» номер
- •Компиляция проекта
- •Инициализация модуля
- •Структура модуля
- •О совпадении имен
- •Сборочный цех
- •Фирменные библиотеки
- •Динамически загружаемые библиотеки (DLL)
- •Итоги
- •Глава 60 Мелкие хитрости
- •Включаемые файлы
- •Условная компиляция
- •Итоги
- •Глава 61 «Кубики» программиста (ООП)
- •Фокус-покус
- •Вместо паяльника
- •На трех китах
- •Инкапсуляция
- •Наследование
- •Приборостроение
- •Гражданское строительство
- •Динамические объекты
- •Полиморфизм
- •Сокрытие полей и методов
- •Итоги
- •Глава 62 Всё только начинается!
- •Крупицы мастерства
- •Программисты, на старт!
- •Приложение А Установка и настройка IDE Borland Pascal
- •Borland Pascal, состав дистрибутива
- •Borland Pascal
- •Установка
- •Организация рабочей папки
- •Создание и настройка ярлыка
- •Пробный запуск
- •Предварительная настройка
- •Русификация консольного окна
- •Turbo Pascal School Pak
- •Приложение Б Консольная программа в среде Delphi
- •Создание пустого консольного приложения
- •Настройка и сохранение консольного приложения
- •Русификация консольного приложения
- •Приложение В Особенности IDE Pascal ABCNet
- •Приложение Ж Директивы управления компиляцией
- •Приложение З Назначение пунктов меню
- •Приложение И Стандартная кодировка символов MS-DOS
- •Приложение К Некоторые встроенные процедуры и функции
- •Приложение М Пример олимпиадной задачи
- •Библиография

Глава 57 Графомания
Я чуть не забыл о придворном программисте Нике! В 49-й главе он решил задачу о минимальной сумме пошлин. Тогда же купцы уговорили его взяться за программу для поиска кратчайшего маршрута между двумя странами. Купцы страдали от пошлин и хотели сократить свои расходы на границах. Ник принял заказ и впал в размышления.
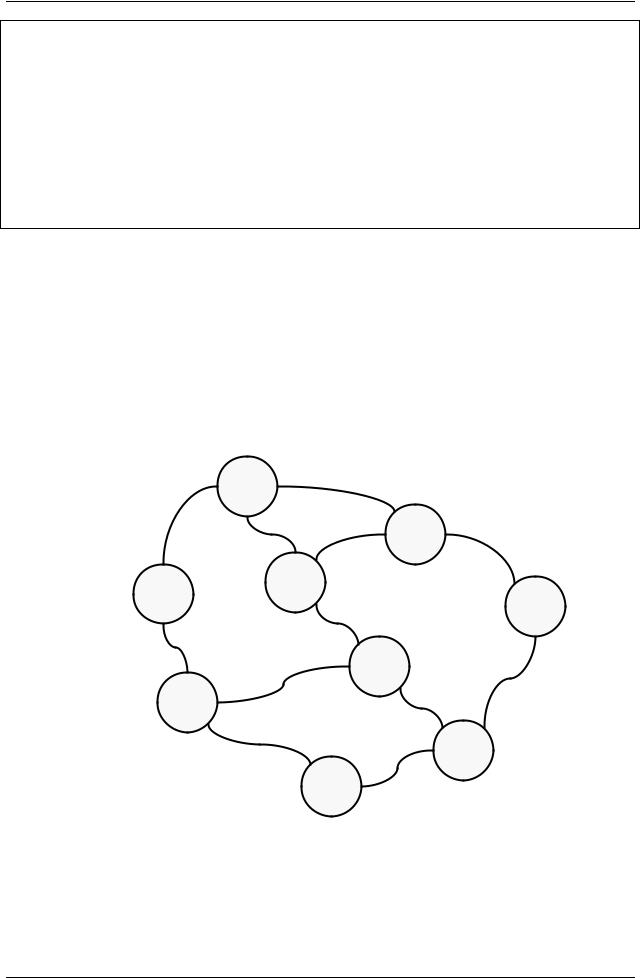
На рис. 130 показан вид из космоса на континент, где проживал Ник. Тамошние страны именовались, как вы помните, латинскими буквами.
H
B
C
I
G A
D
F
E
Рис. 130 – Карта континента
Программа, что создал Ник в 38-й главе, превратила эту карту в следующий файл.
450
Глава 57
Графомания
A B D F I
B A C I H
C B D
D A C E
E D F
F A E G
G H I F
H G I B
I A B G H
В каждой строке файла представлены соседи одной страны: первый символ — это название самой страны, а последующие — её соседи, перечисленные в произвольном порядке. В любом порядке могут следовать и сами строки, — от этого карта не изменится, согласны? Итак, этот файл содержал данные для поиска кратчайшего маршрута.
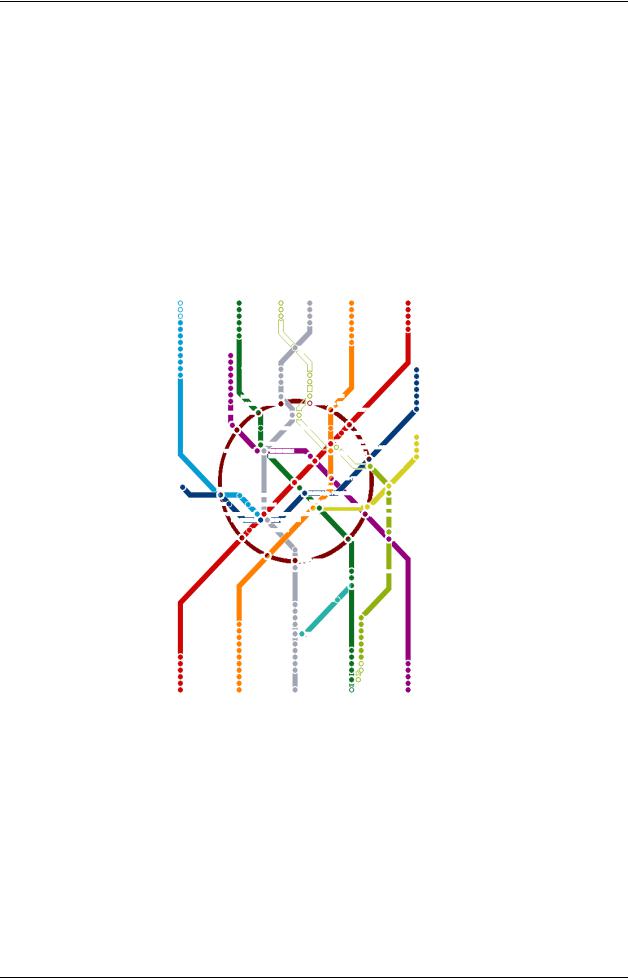
Данные были, только решение куда-то ускользало. Вот берег озера, где спрятался Ник. Его рука в который раз царапает на мокром песке одну и ту же картинку (рис. 131).
H
B
G  I
I  C
C
A
F
D
E
Рис. 131 – Картинка на мокром песке
Здесь вместо разделяющих царства границ, Ник нацарапал соединяющие их дороги. «Вот по этим дорогам поедут купцы, — размышлял он, — но как именно?». Озарение явилось внезапно. «Постой-ка, мне знакома эта картинка! Неужто граф? Я что-то читал о них, надо бы вспомнить!». Оставим ненадолго озаренного Ника, и выясним, что это за штука такая — граф?
451
Глава 57
Графомания
Видимое представление графа
Слово «граф» намекает на рисование, графику. Но программисты и математики признают графом не любую картинку. Граф для них — это сеть связанных между собой объектов. Объекты называют вершинами или узлами графа, а связи между ними — ребрами или дугами. В англоязычной литературе
используют термины Node — узел, и Link — связь.
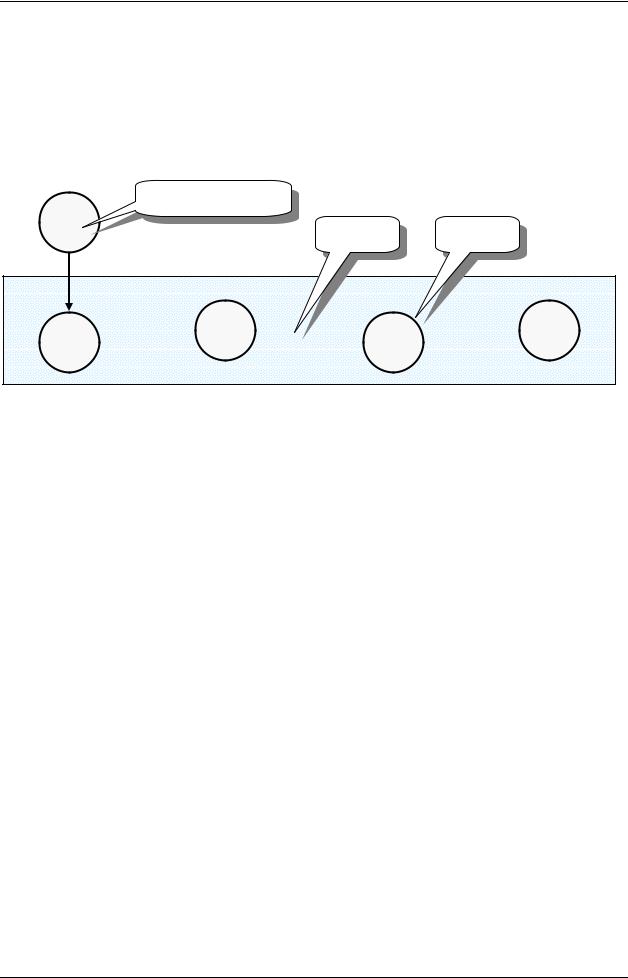
Вот знакомая картинка — схема московского метро (Рис. 132), это пример графа. Здесь станции являются узлами графа, а пути между ними — ребрами. Соседние узлы графа называют смежными. Кстати, нырнувший в метро пассажир решает ту же задачу, что и Ник: ищет кратчайший путь между двумя станциями.
Рис. 132 – Схема московского метрополитена – это граф
А вот ещё примеры графов: карта автомобильных дорог, дерево родственных связей, электрическая схема. Вы можете придумать свои примеры. Или взять нацарапанный Ником рисунок, где узлами являются страны, а ребрами — дороги, их соединяющие.
Мы рассмотрели внешнее, видимое представлении графа, теперь обратимся к его внутреннему представлению в памяти компьютера.
452
Глава 57
Графомания
Внутреннее представление графа
С внутренним представлением графа вы отчасти знакомы. Не удивляйтесь, ведь односвязный список — это тоже граф. Элементы списка — это узлы графа, а связи между элементами — это ребра. И хотя связь между узлами списка однонаправленная, такие графы тоже имеют право на жизнь. Разве нет дорог с односторонним движением?
Голова списка
Ребро Узел
A  B
B  C
C  D
D
Рис. 133 – Односвязный список – это разновидность графа
Годится ли такой список для представления графа, нацарапанного Ником? Рисунок на песке очевидно сложнее списка, — в нём много связей между узлами. К тому же связи на схеме Ника двунаправленные, ведь по дорогам можно ехать в обе стороны. Для представления такого графа требуется что-то похитрее списка. Но в этой замысловатой конструкции найдется место и односвязным спискам.
Приступим к постройке нужного нам графа, и начнем с узла. Представим его, как обычно, записью. Что будет полезной нагрузкой узла? Пока достаточно хранить в записи лишь имя страны, то есть один символ. По мере необходимости, мы добавим в запись и другие поля.
Теперь о связях. Очевидно, что их представим указателями. Но сколько их потребуется? Ведь из разных узлов исходит разное количество связей (рис. 131). Я предлагаю поместить в каждом узле список его связей с соседями. Неслабый получается узелок — с собственным списком внутри! Устройство этого списка связей мы обсудим чуть позже.
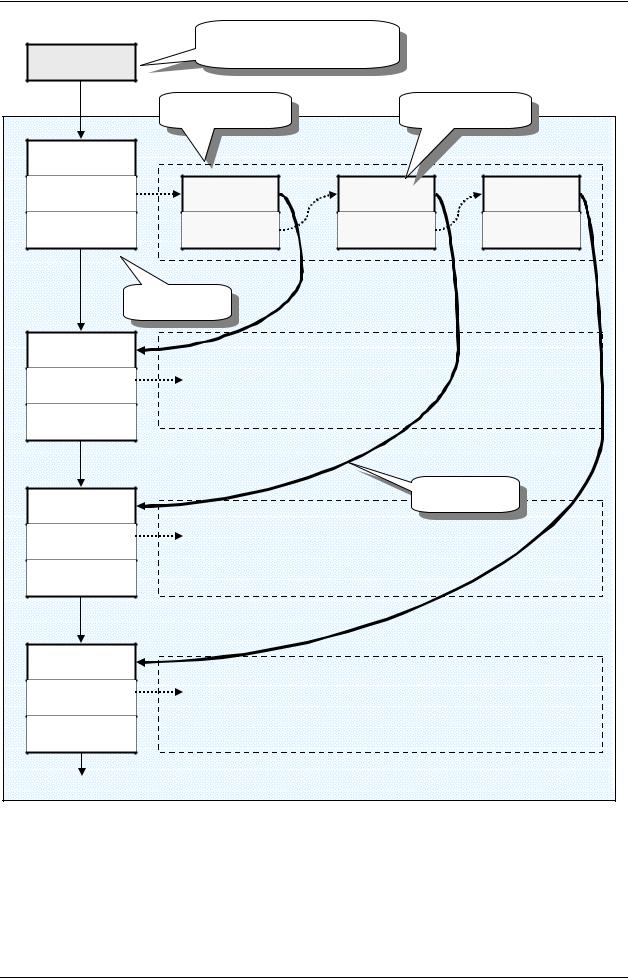
Но и это не всё. Поскольку узлы графа погружаются в кучу, нужно средство для доступа к ним. Вы знаете его — это односвязный список. Значит, внутри каждого узла нужен указатель mNext для включения узла в этот вспомогательный список. В итоге наших размышлений проясняется внутреннее представление графа, показанное на рис. 134.
453
|
|
Глава 57 |
|
|
|
Графомания |
|
|
Вспомогательный список |
|
|
Голова |
|
узлов |
|
|
|
|
|
|
Список ребер |
|
Элемент связи |
H |
|
|
|
mLink |
mNode |
mNode |
mNode |
mNext |
mNext |
mNext |
NIL |
|
Узел графа |
|
|
G |
|
|
|
mLink |
|
|
|
mNext |
|
|
|
I |
|
|
Ребро графа |
|
|
|
|
mLink |
|
|
|
mNext |
|
|
|
B |
|
|
|
mLink |
|
|
|
mNext |
|
|
|
|
Рис. 134 – Организация связей графа на примере узла H |
||
Слева видны тонкие стрелки, ведущие сверху вниз — это вспомогательный список, на который нанизаны узлы графа. Порядок следования узлов в этом списке не важен, важно лишь то, что двигаясь от головы списка по ссылкам mNext, можно достать любой узел. Этот список не определяет зримых связей между узлами.
454
Глава 57
Графомания
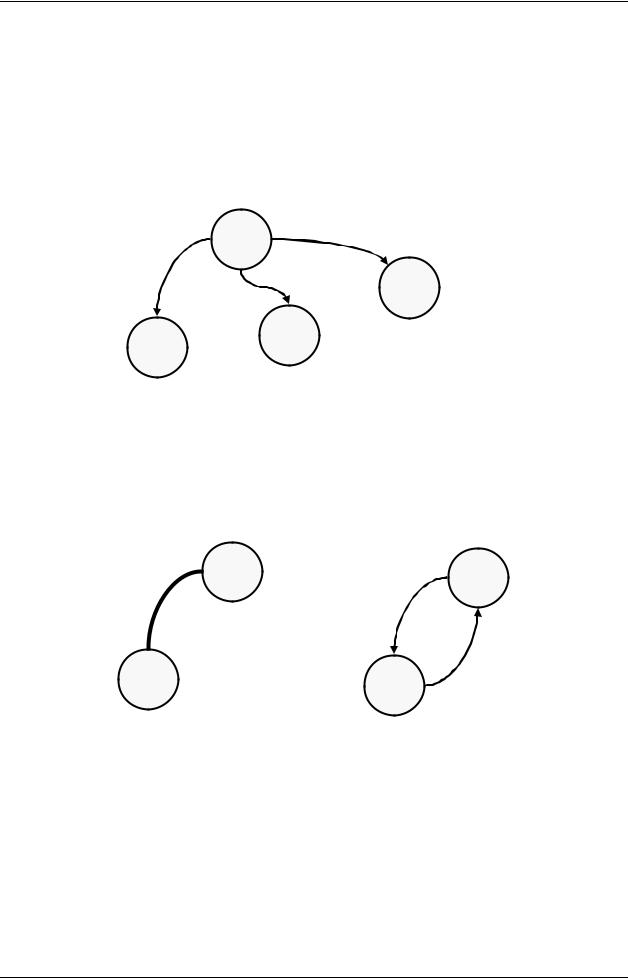
Видимые нам ребра графа формируются списками, что вставлены внутрь каждого узла. Головы этих списков — это поля mLink. Чтобы не загромождать схему, я показал лишь список для узла H. Элементы списка связей вытянулись на схеме слева направо, они сцеплены полями mNext, — не путайте их с полями mNext в узлах графа. Полезной нагрузкой элементов списка связей будут указатели mNode, ссылающиеся на соседние узлы. Именно эти ссылки, показанные на схеме жирными стрелками, определяют видимую форму графа, то есть его ребра. На рис. 135 показана часть графа, соответствующая схеме рис. 134.
H
B
G I
Рис. 135 – Часть графа, соответствующая схеме рис. 134
Здесь показаны лишь ребра, идущие от узла H, но подобные списки содержатся и в других узлах. Например, в списке связей узла G есть ссылка на узел H, поскольку узлы взаимно связаны. Так парами указателей создаётся двусторонняя связь узлов G ↔ H (рис. 136).
H H
G G
Рис. 136 – Ребро графа (слева) и внутреннее его представление (справа)
Прежде, чем выразить эту мудреную структуру на Паскале, повторю основные идеи.
∙Узлы графа представлены записями.
∙Каждая запись узла содержит: 1) полезные поля, 2) голову списка ребер и 3) указатель на следующий узел во вспомогательном списке.
∙Полезной нагрузкой в списке ребер являются указатели на смежные узлы графа.
455
