
- •CONTENTS
- •1.1 Introduction
- •1.2 What Is a Computer?
- •1.3 Programs
- •1.4 Operating Systems
- •1.5 Java, World Wide Web, and Beyond
- •1.6 The Java Language Specification, API, JDK, and IDE
- •1.7 A Simple Java Program
- •1.8 Creating, Compiling, and Executing a Java Program
- •1.9 (GUI) Displaying Text in a Message Dialog Box
- •2.1 Introduction
- •2.2 Writing Simple Programs
- •2.3 Reading Input from the Console
- •2.4 Identifiers
- •2.5 Variables
- •2.7 Named Constants
- •2.8 Numeric Data Types and Operations
- •2.9 Problem: Displaying the Current Time
- •2.10 Shorthand Operators
- •2.11 Numeric Type Conversions
- •2.12 Problem: Computing Loan Payments
- •2.13 Character Data Type and Operations
- •2.14 Problem: Counting Monetary Units
- •2.15 The String Type
- •2.16 Programming Style and Documentation
- •2.17 Programming Errors
- •2.18 (GUI) Getting Input from Input Dialogs
- •3.1 Introduction
- •3.2 boolean Data Type
- •3.3 Problem: A Simple Math Learning Tool
- •3.4 if Statements
- •3.5 Problem: Guessing Birthdays
- •3.6 Two-Way if Statements
- •3.7 Nested if Statements
- •3.8 Common Errors in Selection Statements
- •3.9 Problem: An Improved Math Learning Tool
- •3.10 Problem: Computing Body Mass Index
- •3.11 Problem: Computing Taxes
- •3.12 Logical Operators
- •3.13 Problem: Determining Leap Year
- •3.14 Problem: Lottery
- •3.15 switch Statements
- •3.16 Conditional Expressions
- •3.17 Formatting Console Output
- •3.18 Operator Precedence and Associativity
- •3.19 (GUI) Confirmation Dialogs
- •4.1 Introduction
- •4.2 The while Loop
- •4.3 The do-while Loop
- •4.4 The for Loop
- •4.5 Which Loop to Use?
- •4.6 Nested Loops
- •4.7 Minimizing Numeric Errors
- •4.8 Case Studies
- •4.9 Keywords break and continue
- •4.10 (GUI) Controlling a Loop with a Confirmation Dialog
- •5.1 Introduction
- •5.2 Defining a Method
- •5.3 Calling a Method
- •5.4 void Method Example
- •5.5 Passing Parameters by Values
- •5.6 Modularizing Code
- •5.7 Problem: Converting Decimals to Hexadecimals
- •5.8 Overloading Methods
- •5.9 The Scope of Variables
- •5.10 The Math Class
- •5.11 Case Study: Generating Random Characters
- •5.12 Method Abstraction and Stepwise Refinement
- •6.1 Introduction
- •6.2 Array Basics
- •6.3 Problem: Lotto Numbers
- •6.4 Problem: Deck of Cards
- •6.5 Copying Arrays
- •6.6 Passing Arrays to Methods
- •6.7 Returning an Array from a Method
- •6.8 Variable-Length Argument Lists
- •6.9 Searching Arrays
- •6.10 Sorting Arrays
- •6.11 The Arrays Class
- •7.1 Introduction
- •7.2 Two-Dimensional Array Basics
- •7.3 Processing Two-Dimensional Arrays
- •7.4 Passing Two-Dimensional Arrays to Methods
- •7.5 Problem: Grading a Multiple-Choice Test
- •7.6 Problem: Finding a Closest Pair
- •7.7 Problem: Sudoku
- •7.8 Multidimensional Arrays
- •8.1 Introduction
- •8.2 Defining Classes for Objects
- •8.3 Example: Defining Classes and Creating Objects
- •8.4 Constructing Objects Using Constructors
- •8.5 Accessing Objects via Reference Variables
- •8.6 Using Classes from the Java Library
- •8.7 Static Variables, Constants, and Methods
- •8.8 Visibility Modifiers
- •8.9 Data Field Encapsulation
- •8.10 Passing Objects to Methods
- •8.11 Array of Objects
- •9.1 Introduction
- •9.2 The String Class
- •9.3 The Character Class
- •9.4 The StringBuilder/StringBuffer Class
- •9.5 Command-Line Arguments
- •9.6 The File Class
- •9.7 File Input and Output
- •9.8 (GUI) File Dialogs
- •10.1 Introduction
- •10.2 Immutable Objects and Classes
- •10.3 The Scope of Variables
- •10.4 The this Reference
- •10.5 Class Abstraction and Encapsulation
- •10.6 Object-Oriented Thinking
- •10.7 Object Composition
- •10.8 Designing the Course Class
- •10.9 Designing a Class for Stacks
- •10.10 Designing the GuessDate Class
- •10.11 Class Design Guidelines
- •11.1 Introduction
- •11.2 Superclasses and Subclasses
- •11.3 Using the super Keyword
- •11.4 Overriding Methods
- •11.5 Overriding vs. Overloading
- •11.6 The Object Class and Its toString() Method
- •11.7 Polymorphism
- •11.8 Dynamic Binding
- •11.9 Casting Objects and the instanceof Operator
- •11.11 The ArrayList Class
- •11.12 A Custom Stack Class
- •11.13 The protected Data and Methods
- •11.14 Preventing Extending and Overriding
- •12.1 Introduction
- •12.2 Swing vs. AWT
- •12.3 The Java GUI API
- •12.4 Frames
- •12.5 Layout Managers
- •12.6 Using Panels as Subcontainers
- •12.7 The Color Class
- •12.8 The Font Class
- •12.9 Common Features of Swing GUI Components
- •12.10 Image Icons
- •13.1 Introduction
- •13.2 Exception-Handling Overview
- •13.3 Exception-Handling Advantages
- •13.4 Exception Types
- •13.5 More on Exception Handling
- •13.6 The finally Clause
- •13.7 When to Use Exceptions
- •13.8 Rethrowing Exceptions
- •13.9 Chained Exceptions
- •13.10 Creating Custom Exception Classes
- •14.1 Introduction
- •14.2 Abstract Classes
- •14.3 Example: Calendar and GregorianCalendar
- •14.4 Interfaces
- •14.5 Example: The Comparable Interface
- •14.6 Example: The ActionListener Interface
- •14.7 Example: The Cloneable Interface
- •14.8 Interfaces vs. Abstract Classes
- •14.9 Processing Primitive Data Type Values as Objects
- •14.10 Sorting an Array of Objects
- •14.11 Automatic Conversion between Primitive Types and Wrapper Class Types
- •14.12 The BigInteger and BigDecimal Classes
- •14.13 Case Study: The Rational Class
- •15.1 Introduction
- •15.2 Graphical Coordinate Systems
- •15.3 The Graphics Class
- •15.4 Drawing Strings, Lines, Rectangles, and Ovals
- •15.5 Case Study: The FigurePanel Class
- •15.6 Drawing Arcs
- •15.7 Drawing Polygons and Polylines
- •15.8 Centering a String Using the FontMetrics Class
- •15.9 Case Study: The MessagePanel Class
- •15.10 Case Study: The StillClock Class
- •15.11 Displaying Images
- •15.12 Case Study: The ImageViewer Class
- •16.1 Introduction
- •16.2 Event and Event Source
- •16.3 Listeners, Registrations, and Handling Events
- •16.4 Inner Classes
- •16.5 Anonymous Class Listeners
- •16.6 Alternative Ways of Defining Listener Classes
- •16.7 Problem: Loan Calculator
- •16.8 Window Events
- •16.9 Listener Interface Adapters
- •16.10 Mouse Events
- •16.11 Key Events
- •16.12 Animation Using the Timer Class
- •17.1 Introduction
- •17.2 Buttons
- •17.3 Check Boxes
- •17.4 Radio Buttons
- •17.5 Labels
- •17.6 Text Fields
- •17.7 Text Areas
- •17.8 Combo Boxes
- •17.9 Lists
- •17.10 Scroll Bars
- •17.11 Sliders
- •17.12 Creating Multiple Windows
- •18.1 Introduction
- •18.2 Developing Applets
- •18.3 The HTML File and the <applet> Tag
- •18.4 Applet Security Restrictions
- •18.5 Enabling Applets to Run as Applications
- •18.6 Applet Life-Cycle Methods
- •18.7 Passing Strings to Applets
- •18.8 Case Study: Bouncing Ball
- •18.9 Case Study: TicTacToe
- •18.10 Locating Resources Using the URL Class
- •18.11 Playing Audio in Any Java Program
- •18.12 Case Study: Multimedia Animations
- •19.1 Introduction
- •19.2 How is I/O Handled in Java?
- •19.3 Text I/O vs. Binary I/O
- •19.4 Binary I/O Classes
- •19.5 Problem: Copying Files
- •19.6 Object I/O
- •19.7 Random-Access Files
- •20.1 Introduction
- •20.2 Problem: Computing Factorials
- •20.3 Problem: Computing Fibonacci Numbers
- •20.4 Problem Solving Using Recursion
- •20.5 Recursive Helper Methods
- •20.6 Problem: Finding the Directory Size
- •20.7 Problem: Towers of Hanoi
- •20.8 Problem: Fractals
- •20.9 Problem: Eight Queens
- •20.10 Recursion vs. Iteration
- •20.11 Tail Recursion
- •APPENDIXES
- •INDEX
20.6 Problem: Finding the Directory Size 687
The first binarySearch method passes the initial array with low = 0 and high = list.length - 1 to the second binarySearch method. The second method is invoked recursively to find the key in an ever-shrinking subarray.
20.6 Problem: Finding the Directory Size
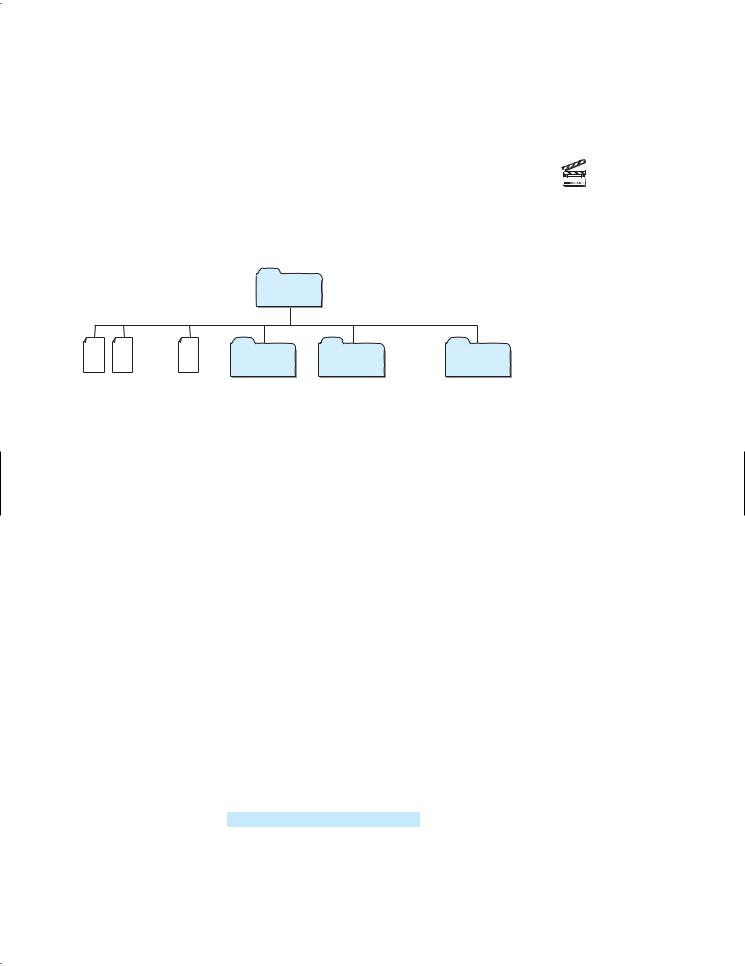
The preceding examples can easily be solved without using recursion. This section presents a problem that is difficult to solve without using recursion. The problem is to find the size of a directory. The size of a directory is the sum of the sizes of all files in the directory. A directory d may contain subdirectories. Suppose a directory contains files f1, f2, Á , fm and subdirectories d1, d2, Á , dn, as shown in Figure 20.5.
Video Note
Directory size
directory
f1 |
f2 |
. . . |
fm |
d1 |
d2 |
. . . |
dn |
|
|
|
|
FIGURE 20.5 A directory contains files and subdirectories.
The size of the directory can be defined recursively as follows:
size1d2 = size1f12 + size1f22 + Á + size1fm2 + size1d12 + size1d22 + Á + size1dn2
The File class, introduced in §9.6, can be used to represent a file or a directory and obtain the properties for files and directories. Two methods in the File class are useful for this problem:
■The length() method returns the size of a file.
■The listFiles() method returns an array of File objects under a directory.
Listing 20.7 gives a program that prompts the user to enter a directory or a file and displays its size.
LISTING 20.7 DirectorySize.java
1 import java.io.File;
2 import java.util.Scanner;
3
4 public class DirectorySize {
5public static void main(String[] args) {
6 |
|
// Prompt the user to enter a directory or a file |
|
||||
7 |
|
System.out.print("Enter a directory or a file: "); |
|
||||
8 |
|
Scanner input = new Scanner(System.in); |
|
||||
9 |
|
String directory = input.nextLine(); |
|
||||
10 |
|
|
|
|
|
|
|
11 |
|
// Display the size |
|
||||
12 |
|
System.out.println(getSize(new File(directory)) |
+ " bytes"); |
invoke method |
|||
13 |
} |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
15 |
|
public static long getSize(File file) { |
|
|
getSize method |
||
16 |
|
long size = 0; // Store the total size of all files |
|
||||
17 |
|
|
|
|
|
|
|
18 |
|
if |
(file.isDirectory() |
) { |
|
|
is directory? |
688 Chapter 20 |
Recursion |
|||||
|
|
|
|
|||
all subitems |
19 |
|
File[] files = file.listFiles(); |
// All files and subdirectories |
||
|
20 |
|
for (int i = 0; i < files.length; i++) { |
|||
recursive call |
21 |
|
size += |
getSize(files[i]) |
; // Recursive call |
|
|
22 |
} |
|
|
|
|
|
23 |
} |
|
|
|
|
base case |
24 |
else { // Base case |
||||
|
25 |
|
size += file.length(); |
|||
|
26 |
} |
|
|
|
|
|
27 |
|
|
|
|
|
|
28 |
return size; |
||||
|
29 |
} |
|
|
|
|
|
30 |
} |
|
|
|
|
Enter a directory or a file: c:\book 48619631 bytes
Enter a directory or a file: c:\book\Welcome.java 172 bytes
Enter a directory or a file: c:\book\NonExistentFile 0 bytes
If the file object represents a directory (line 18), each subitem (file or subdirectory) in the directory is recursively invoked to obtain its size (line 21). If the file object represents a file (line 24), the file size is obtained (line 25).
What happens if an incorrect or a nonexistent directory is entered? The program will detect that it is not a directory and invoke file.length() (line 25), which returns 0. So, in this case, the getSize method will return 0.
|
Tip |
testing base cases |
To avoid mistakes, it is a good practice to test base cases. For example, you should test the pro- |
|
gram for an input of file, an empty directory, a nonexistent directory, and a nonexistent file. |
20.7 Problem: Towers of Hanoi
The Towers of Hanoi problem is a classic problem that can be solved easily using recursion but is difficult to solve otherwise.
The problem involves moving a specified number of disks of distinct sizes from one tower to another while observing the following rules:
■There are n disks labeled 1, 2, 3, Á , n and three towers labeled A, B, and C.
■No disk can be on top of a smaller disk at any time.
■All the disks are initially placed on tower A.
■Only one disk can be moved at a time, and it must be the top disk on a tower.
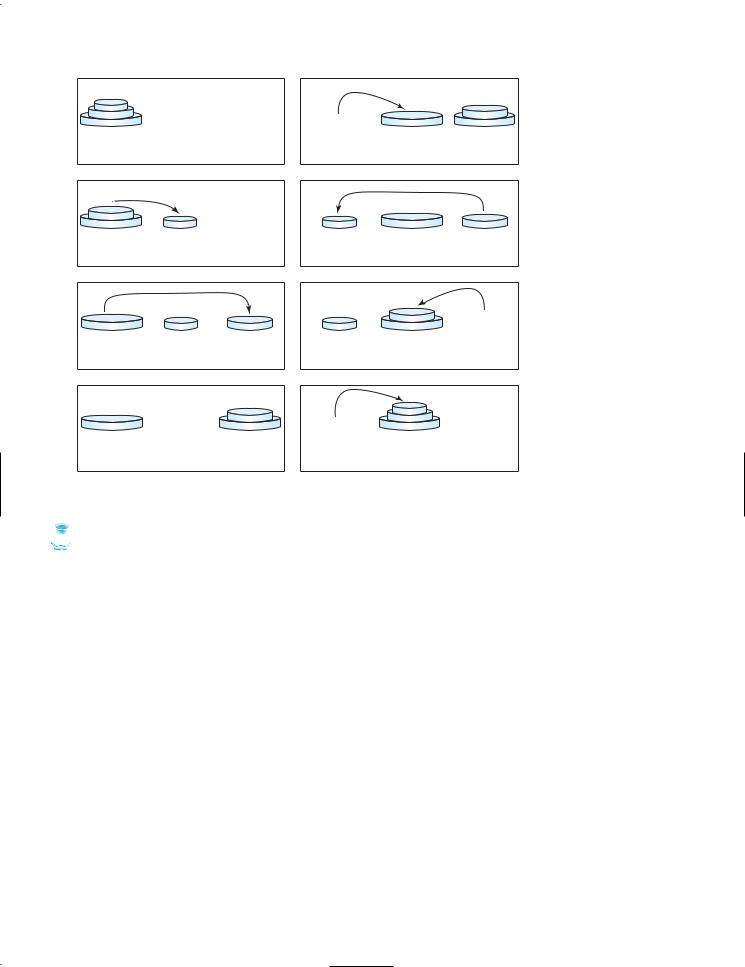
The objective of the problem is to move all the disks from A to B with the assistance of C. For example, if you have three disks, the steps to move all of the disks from A to B are shown in Figure 20.6.
20.7 Problem: Towers of Hanoi 689
A |
B |
C |
A |
B |
C |
|
Original position |
|
Step 4: Move disk 3 from A to B |
||
A |
B |
C |
A |
B |
C |
Step 1: Move disk 1 from A to B |
Step 5: Move disk 1 from C to A |
||||
A |
B |
C |
A |
B |
C |
Step 2: Move disk 2 from A to C |
Step 6: Move disk 2 from C to B |
||||
A |
B |
C |
A |
B |
C |
Step 3: Move disk 1 from B to C |
Step 7: Move disk 1 from A to B |
||||
FIGURE 20.6 The goal of the Towers of Hanoi problem is to move disks from tower A to tower B without breaking the rules.
 Note
Note
The Towers of Hanoi is a classic computer-science problem, to which many Websites are devoted.
One of them worth looking at is www.cut-the-knot.com/recurrence/hanoi.html.
In the case of three disks, you can find the solution manually. For a larger number of disks, however—even for four—the problem is quite complex. Fortunately, the problem has an inherently recursive nature, which leads to a straightforward recursive solution.
The base case for the problem is n = 1. If n == 1, you could simply move the disk from A to B. When n > 1, you could split the original problem into three subproblems and solve them sequentially.
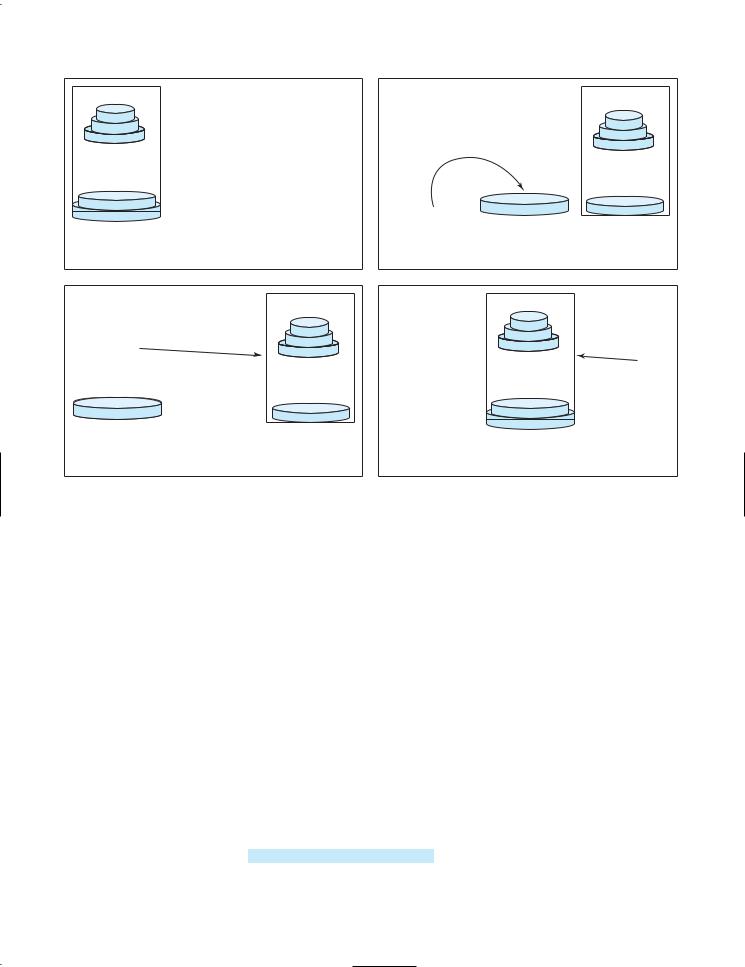
1.Move the first n - 1 disks from A to C with the assistance of tower B, as shown in Step 1 in Figure 20.7.
2.Move disk n from A to B, as shown in Step 2 in Figure 20.7.
3.Move n - 1 disks from C to B with the assistance of tower A, as shown in Step 3 in Figure 20.7.
The following method moves n disks from the fromTower to the toTower with the assistance of the auxTower:
void moveDisks(int n, char fromTower, char toTower, char auxTower)
The algorithm for the method can be described as follows:
if (n == 1) // Stopping condition
Move disk 1 from the fromTower to the toTower; else {
690 Chapter 20 Recursion
n – 1 disks |
n – 1 disks |
. |
|
|
|
|
. |
. |
|
|
|
|
|
|
|
|
|
. |
|
. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
A |
B |
C |
A |
B |
C |
|
Original position |
|
|
Step2: Move disk n from A to B |
|
|
|
n – 1 disks |
|
n – 1 disks |
|
|
|
. |
|
. |
|
|
|
|
. |
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
A |
B |
C |
A |
B |
C |
Step 1: Move the first n – 1 disks from A to C recursively |
Step3: Move n – 1 disks from C to B recursively |
||||
FIGURE 20.7 The Towers of Hanoi problem can be decomposed into three subproblems.
moveDisks(n - 1, fromTower, auxTower, toTower); Move disk n from the fromTower to the toTower; moveDisks(n - 1, auxTower, toTower, fromTower);
}
Listing 20.8 gives a program that prompts the user to enter the number of disks and invokes the recursive method moveDisks to display the solution for moving the disks.
LISTING 20.8 TowersOfHanoi.java
1 import java.util.Scanner;
2
3 public class TowersOfHanoi {
4/** Main method */
5 public static void main(String[] args) {
6// Create a Scanner
7Scanner input = new Scanner(System.in);
8 System.out.print("Enter number of disks: ");
9 int n = input.nextInt();
10
11// Find the solution recursively
12System.out.println("The moves are:");
13moveDisks(n, 'A', 'B', 'C');
14}
15
16/** The method for finding the solution to move n disks
17from fromTower to toTower with auxTower */
20.7 Problem: Towers of Hanoi 691
18public static void moveDisks(int n, char fromTower,
19char toTower, char auxTower) {
20 |
if (n == 1) // Stopping condition |
base case |
21System.out.println("Move disk " + n + " from " +
22fromTower + " to " + toTower);
23else {
24 |
moveDisks(n - 1, fromTower, auxTower, toTower); |
recursion |
25System.out.println("Move disk " + n + " from " +
26fromTower + " to " + toTower);
27 |
moveDisks(n - 1, auxTower, toTower, fromTower) ; |
recursion |
28}
29}
30}
Enter number of disks: 4
The moves are:
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C
Move disk 4 from A to B
Move disk 1 from C to B
Move disk 2 from C to A
Move disk 1 from B to A
Move disk 3 from C to B
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
This problem is inherently recursive. Using recursion makes it possible to find a natural, simple solution. It would be difficult to solve the problem without using recursion.
Consider tracing the program for n = 3. The successive recursive calls are shown in Figure 20.8. As you can see, writing the program is easier than tracing the recursive calls. The system uses stacks to trace the calls behind the scenes. To some extent, recursion provides a level of abstraction that hides iterations and other details from the user.
|
moveDisks(3,'A','B','C') |
|
|
|
moveDisks(2,'A','C','B') |
|
|
|
move disk 3 from A to B |
|
|
|
moveDisks(2,'C','B','A') |
|
|
moveDisks(2,'A','C','B') |
moveDisks(2,'C','B','A') |
||
moveDisks(1,'A','B','C') |
moveDisks(1,'C','A','B') |
||
move disk 2 from A to C |
move disk 2 from C to B |
||
moveDisks(1,'B','C','A') |
moveDisks(1,'A','B','C') |
||
moveDisks(1,'A','B','C') |
moveDisks(1,'B','C','A') |
moveDisks(1,'C','A','B') |
moveDisks(1,'A','B','C') |
move disk 1 from A to B |
move disk 1 from B to C |
move disk 1 from C to A |
move disk 1 from A to B |
FIGURE 20.8 Invoking moveDisks(3, 'A', 'B', 'C') spawns calls to moveDisks recursively.
