
- •CONTENTS
- •1.1 Introduction
- •1.2 What Is a Computer?
- •1.3 Programs
- •1.4 Operating Systems
- •1.5 Java, World Wide Web, and Beyond
- •1.6 The Java Language Specification, API, JDK, and IDE
- •1.7 A Simple Java Program
- •1.8 Creating, Compiling, and Executing a Java Program
- •1.9 (GUI) Displaying Text in a Message Dialog Box
- •2.1 Introduction
- •2.2 Writing Simple Programs
- •2.3 Reading Input from the Console
- •2.4 Identifiers
- •2.5 Variables
- •2.7 Named Constants
- •2.8 Numeric Data Types and Operations
- •2.9 Problem: Displaying the Current Time
- •2.10 Shorthand Operators
- •2.11 Numeric Type Conversions
- •2.12 Problem: Computing Loan Payments
- •2.13 Character Data Type and Operations
- •2.14 Problem: Counting Monetary Units
- •2.15 The String Type
- •2.16 Programming Style and Documentation
- •2.17 Programming Errors
- •2.18 (GUI) Getting Input from Input Dialogs
- •3.1 Introduction
- •3.2 boolean Data Type
- •3.3 Problem: A Simple Math Learning Tool
- •3.4 if Statements
- •3.5 Problem: Guessing Birthdays
- •3.6 Two-Way if Statements
- •3.7 Nested if Statements
- •3.8 Common Errors in Selection Statements
- •3.9 Problem: An Improved Math Learning Tool
- •3.10 Problem: Computing Body Mass Index
- •3.11 Problem: Computing Taxes
- •3.12 Logical Operators
- •3.13 Problem: Determining Leap Year
- •3.14 Problem: Lottery
- •3.15 switch Statements
- •3.16 Conditional Expressions
- •3.17 Formatting Console Output
- •3.18 Operator Precedence and Associativity
- •3.19 (GUI) Confirmation Dialogs
- •4.1 Introduction
- •4.2 The while Loop
- •4.3 The do-while Loop
- •4.4 The for Loop
- •4.5 Which Loop to Use?
- •4.6 Nested Loops
- •4.7 Minimizing Numeric Errors
- •4.8 Case Studies
- •4.9 Keywords break and continue
- •4.10 (GUI) Controlling a Loop with a Confirmation Dialog
- •5.1 Introduction
- •5.2 Defining a Method
- •5.3 Calling a Method
- •5.4 void Method Example
- •5.5 Passing Parameters by Values
- •5.6 Modularizing Code
- •5.7 Problem: Converting Decimals to Hexadecimals
- •5.8 Overloading Methods
- •5.9 The Scope of Variables
- •5.10 The Math Class
- •5.11 Case Study: Generating Random Characters
- •5.12 Method Abstraction and Stepwise Refinement
- •6.1 Introduction
- •6.2 Array Basics
- •6.3 Problem: Lotto Numbers
- •6.4 Problem: Deck of Cards
- •6.5 Copying Arrays
- •6.6 Passing Arrays to Methods
- •6.7 Returning an Array from a Method
- •6.8 Variable-Length Argument Lists
- •6.9 Searching Arrays
- •6.10 Sorting Arrays
- •6.11 The Arrays Class
- •7.1 Introduction
- •7.2 Two-Dimensional Array Basics
- •7.3 Processing Two-Dimensional Arrays
- •7.4 Passing Two-Dimensional Arrays to Methods
- •7.5 Problem: Grading a Multiple-Choice Test
- •7.6 Problem: Finding a Closest Pair
- •7.7 Problem: Sudoku
- •7.8 Multidimensional Arrays
- •8.1 Introduction
- •8.2 Defining Classes for Objects
- •8.3 Example: Defining Classes and Creating Objects
- •8.4 Constructing Objects Using Constructors
- •8.5 Accessing Objects via Reference Variables
- •8.6 Using Classes from the Java Library
- •8.7 Static Variables, Constants, and Methods
- •8.8 Visibility Modifiers
- •8.9 Data Field Encapsulation
- •8.10 Passing Objects to Methods
- •8.11 Array of Objects
- •9.1 Introduction
- •9.2 The String Class
- •9.3 The Character Class
- •9.4 The StringBuilder/StringBuffer Class
- •9.5 Command-Line Arguments
- •9.6 The File Class
- •9.7 File Input and Output
- •9.8 (GUI) File Dialogs
- •10.1 Introduction
- •10.2 Immutable Objects and Classes
- •10.3 The Scope of Variables
- •10.4 The this Reference
- •10.5 Class Abstraction and Encapsulation
- •10.6 Object-Oriented Thinking
- •10.7 Object Composition
- •10.8 Designing the Course Class
- •10.9 Designing a Class for Stacks
- •10.10 Designing the GuessDate Class
- •10.11 Class Design Guidelines
- •11.1 Introduction
- •11.2 Superclasses and Subclasses
- •11.3 Using the super Keyword
- •11.4 Overriding Methods
- •11.5 Overriding vs. Overloading
- •11.6 The Object Class and Its toString() Method
- •11.7 Polymorphism
- •11.8 Dynamic Binding
- •11.9 Casting Objects and the instanceof Operator
- •11.11 The ArrayList Class
- •11.12 A Custom Stack Class
- •11.13 The protected Data and Methods
- •11.14 Preventing Extending and Overriding
- •12.1 Introduction
- •12.2 Swing vs. AWT
- •12.3 The Java GUI API
- •12.4 Frames
- •12.5 Layout Managers
- •12.6 Using Panels as Subcontainers
- •12.7 The Color Class
- •12.8 The Font Class
- •12.9 Common Features of Swing GUI Components
- •12.10 Image Icons
- •13.1 Introduction
- •13.2 Exception-Handling Overview
- •13.3 Exception-Handling Advantages
- •13.4 Exception Types
- •13.5 More on Exception Handling
- •13.6 The finally Clause
- •13.7 When to Use Exceptions
- •13.8 Rethrowing Exceptions
- •13.9 Chained Exceptions
- •13.10 Creating Custom Exception Classes
- •14.1 Introduction
- •14.2 Abstract Classes
- •14.3 Example: Calendar and GregorianCalendar
- •14.4 Interfaces
- •14.5 Example: The Comparable Interface
- •14.6 Example: The ActionListener Interface
- •14.7 Example: The Cloneable Interface
- •14.8 Interfaces vs. Abstract Classes
- •14.9 Processing Primitive Data Type Values as Objects
- •14.10 Sorting an Array of Objects
- •14.11 Automatic Conversion between Primitive Types and Wrapper Class Types
- •14.12 The BigInteger and BigDecimal Classes
- •14.13 Case Study: The Rational Class
- •15.1 Introduction
- •15.2 Graphical Coordinate Systems
- •15.3 The Graphics Class
- •15.4 Drawing Strings, Lines, Rectangles, and Ovals
- •15.5 Case Study: The FigurePanel Class
- •15.6 Drawing Arcs
- •15.7 Drawing Polygons and Polylines
- •15.8 Centering a String Using the FontMetrics Class
- •15.9 Case Study: The MessagePanel Class
- •15.10 Case Study: The StillClock Class
- •15.11 Displaying Images
- •15.12 Case Study: The ImageViewer Class
- •16.1 Introduction
- •16.2 Event and Event Source
- •16.3 Listeners, Registrations, and Handling Events
- •16.4 Inner Classes
- •16.5 Anonymous Class Listeners
- •16.6 Alternative Ways of Defining Listener Classes
- •16.7 Problem: Loan Calculator
- •16.8 Window Events
- •16.9 Listener Interface Adapters
- •16.10 Mouse Events
- •16.11 Key Events
- •16.12 Animation Using the Timer Class
- •17.1 Introduction
- •17.2 Buttons
- •17.3 Check Boxes
- •17.4 Radio Buttons
- •17.5 Labels
- •17.6 Text Fields
- •17.7 Text Areas
- •17.8 Combo Boxes
- •17.9 Lists
- •17.10 Scroll Bars
- •17.11 Sliders
- •17.12 Creating Multiple Windows
- •18.1 Introduction
- •18.2 Developing Applets
- •18.3 The HTML File and the <applet> Tag
- •18.4 Applet Security Restrictions
- •18.5 Enabling Applets to Run as Applications
- •18.6 Applet Life-Cycle Methods
- •18.7 Passing Strings to Applets
- •18.8 Case Study: Bouncing Ball
- •18.9 Case Study: TicTacToe
- •18.10 Locating Resources Using the URL Class
- •18.11 Playing Audio in Any Java Program
- •18.12 Case Study: Multimedia Animations
- •19.1 Introduction
- •19.2 How is I/O Handled in Java?
- •19.3 Text I/O vs. Binary I/O
- •19.4 Binary I/O Classes
- •19.5 Problem: Copying Files
- •19.6 Object I/O
- •19.7 Random-Access Files
- •20.1 Introduction
- •20.2 Problem: Computing Factorials
- •20.3 Problem: Computing Fibonacci Numbers
- •20.4 Problem Solving Using Recursion
- •20.5 Recursive Helper Methods
- •20.6 Problem: Finding the Directory Size
- •20.7 Problem: Towers of Hanoi
- •20.8 Problem: Fractals
- •20.9 Problem: Eight Queens
- •20.10 Recursion vs. Iteration
- •20.11 Tail Recursion
- •APPENDIXES
- •INDEX
20.11 Tail Recursion 697
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
|
check |
|
|
|
|
|
|
1 |
|
colum |
|
|
|
|
|
|
|
|
upright diagonal |
|
|
||||
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
search(row) |
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
(a) |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
check |
|
|
|
|
|
|
|
1 |
colum |
|
|
|
|
|
|
|
|
|
|
|
upright diagonal |
||||
2 |
|
|
|
|
||||
upleft |
|
|
|
|
|
|
||
3 |
|
|
|
|
|
search(row) |
||
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
(c) |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
|
|
check |
|
|
|
|
|
1 |
upleft |
colum |
|
|
|
|
|
|
|
upright diagonal |
|
||||||
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
check |
|
1 |
colum |
|
2 |
upright diagonal |
|
3 |
||
|
||
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
|
(d) |
 search(row)
search(row)
 search(row 1)
search(row 1)
FIGURE 20.12 Invoking search(row) fills in a queen in a column on the row.
20.10 Recursion vs. Iteration
Recursion is an alternative form of program control. It is essentially repetition without a loop. |
|
When you use loops, you specify a loop body. The repetition of the loop body is controlled by |
|
the loop control structure. In recursion, the method itself is called repeatedly. A selection |
|
statement must be used to control whether to call the method recursively or not. |
|
Recursion bears substantial overhead. Each time the program calls a method, the system |
recursion overhead |
must assign space for all of the method’s local variables and parameters. This can consume |
|
considerable memory and requires extra time to manage the additional space. |
|
Any problem that can be solved recursively can be solved nonrecursively with iterations. |
|
Recursion has some negative aspects: it uses up too much time and too much memory. Why, |
recursion advantages |
then, should you use it? In some cases, using recursion enables you to specify for an inher- |
|
ently recursive problem a clear, simple solution that would otherwise be difficult to obtain. |
|
Examples are the directory-size problem, the Towers of Hanoi problem, and the fractal prob- |
|
lem, which are rather difficult to solve without using recursion. |
|
The decision whether to use recursion or iteration should be based on the nature of, and your |
recursion or iteration? |
understanding of, the problem you are trying to solve. The rule of thumb is to use whichever |
|
approach can best develop an intuitive solution that naturally mirrors the problem. If an iterative |
|
solution is obvious, use it. It will generally be more efficient than the recursive option. |
|
 Note
Note
Your recursive program could run out of memory, causing a StackOverflowError. StackOverflowError
 Tip
Tip
If you are concerned about your program’s performance, avoid using recursion, because it takes |
performance concern |
more time and consumes more memory than iteration. |
|
20.11 Tail Recursion
A recursive method is said to be tail recursive if there are no pending operations to be performed on return from a recursive call. For example, the recursive isPalindrome method

698 Chapter 20 Recursion
(lines 6–13) in Listing 20.4 is tail recursive because there are no pending operations after recursively invoking isPalindrome in line 12. However, the recursive factorial method (lines 16-21) in Listing 20.1 is not tail recursive, because there is a pending operation, namely multiplication, to be performed on return from each recursive call.
Tail recursion is desirable, because the method ends when the last recursive call ends. So there is no need to store the intermediate calls in the stack. Some compilers can optimize tail recursion to reduce stack space.
A non-tail-recursive method can often be converted to a tail-recursive method by using auxiliary parameters. These parameters are used to contain the result. The idea is to incorporate the pending operations into the auxiliary parameters in such a way that the recursive call no longer has a pending operation. You may define a new auxiliary recursive method with the auxiliary parameters. This method may overload the original method with the same name but a different signature. For example, the factorial method in Listing 20.1 can be written in a tail-recursive way as follows:
|
1 |
/** Return the factorial for a specified number */ |
original method |
2 |
public static long factorial(int n) { |
invoke auxiliary method |
3 |
return factorial(n, 1); // Call auxiliary method |
|
4 |
} |
|
5 |
|
|
6 |
/** Auxiliary tail-recursive method for factorial */ |
auxiliary method |
7 |
private static long factorial(int n, int result) { |
|
8 |
if (n == 1) |
|
9 |
return result; |
|
10 |
else |
recursive call |
11 |
return factorial(n - 1, n * result); // Recursive call |
|
12 |
} |
The first factorial method simply invokes the second auxiliary method (line 3). The second method contains an auxiliary parameter result that stores the result for factorial of n. This method is invoked recursively in line 11. There is no pending operation after a call is returned. The final result is returned in line 9, which is also the return value from invoking factorial(n, 1) in line 3.
KEY TERMS
base case 678 infinite recursion 679 recursive method 678
recursive helper method 685 stopping condition 678
tail recursion 697
CHAPTER SUMMARY
1.A recursive method is one that directly or indirectly invokes itself. For a recursive method to terminate, there must be one or more base cases.
2.Recursion is an alternative form of program control. It is essentially repetition without a loop control. It can be used to specify simple, clear solutions for inherently recursive problems that would otherwise be difficult to solve.
3.Sometimes the original method needs to be modified to receive additional parameters in order to be invoked recursively. A recursive helper method can be defined for this purpose.
4.Recursion bears substantial overhead. Each time the program calls a method, the system must assign space for all of the method’s local variables and parameters. This can consume considerable memory and requires extra time to manage the additional space.
5.A recursive method is said to be tail recursive if there are no pending operations to be performed on return from a recursive call. Some compilers can optimize tail recursion to reduce stack space.
Review Questions 699
REVIEW QUESTIONS
Sections 20.1–20.3
20.1What is a recursive method? Describe the characteristics of recursive methods. What is an infinite recursion?
20.2Write a recursive mathematical definition for computing 2n for a positive integer n.
20.3Write a recursive mathematical definition for computing xn for a positive integer n and a real number x.
20.4Write a recursive mathematical definition for computing 1 + 2 + 3 + Á + n for a positive integer.
20.5How many times is the factorial method in Listing 20.1 invoked for factorial(6)?
20.6How many times is the fib method in Listing 20.2 invoked for fib(6)?
Sections 20.4–20.6
20.7Show the call stack for isPalindrome("abcba") using the methods defined in Listing 20.3 and Listing 20.4, respectively.
20.8Show the call stack for selectionSort(new double[]{2, 3, 5, 1}) using the method defined in Listing 20.5.
20.9What is a recursive helper method?
Section 20.7
20.10How many times is the moveDisks method in Listing 20.8 invoked for moveDisks(5, 'A', 'B', 'C')?
Section 20.9
20.11Which of the following statements are true?
■Any recursive method can be converted into a nonrecursive method.
■Recursive methods take more time and memory to execute than nonrecursive methods.
■Recursive methods are always simpler than nonrecursive methods.
■There is always a selection statement in a recursive method to check whether a base case is reached.
20.12What is the cause for the stack-overflow exception?
Comprehensive
20.13 Show the output of the following program:
public class Test {
public static void main(String[] args) { System.out.println(
"Sum is " + xMethod(5));
}
public static int xMethod(int n) { if (n == 1)
return 1; else
return n + xMethod(n - 1);
}
}
public class Test {
public static void main(String[] args) { xMethod(1234567);
}
public static void xMethod(int n) { if (n > 0) {
System.out.print(n % 10); xMethod(n / 10);
}
}
}

700 Chapter 20 Recursion
20.14 Show the output of the following two programs:
public class Test {
public static void main(String[] args) { xMethod(5);
}
public static void xMethod(int n) { if (n > 0) {
System.out.print(n + " "); xMethod(n - 1);
}
}
}
public class Test {
public static void main(String[] args) { xMethod(5);
}
public static void xMethod(int n) { if (n > 0) {
xMethod(n - 1); System.out.print(n + " ");
}
}
}
20.15 What is wrong in the following method?
public class Test {
public static void main(String[] args) { xMethod(1234567);
}
public static void xMethod(double n) { if (n != 0) {
System.out.print(n); xMethod(n / 10);
}
}
}
public class Test {
public static void main(String[] args) { Test test = new Test(); System.out.println(test.toString());
}
public Test() {
Test test = new Test();
}
}
20.16Identify tail-recursive methods in this chapter.
20.17Rewrite the fib method in Listing 20.2 using tail recursion.
PROGRAMMING EXERCISES
Sections 20.2–20.3
20.1* (Factorial) Using the BigInteger class introduced in §14.12, you can find the factorial for a large number (e.g., 100!). Write a program that prompts the user to enter an integer and displays its factorial. Implement the method using recursion.
20.2* (Fibonacci numbers) Rewrite the fib method in Listing 20.2 using iterations.
Hint: To compute fib(n) without recursion, you need to obtain fib(n - 2) and fib(n - 1) first. Let f0 and f1 denote the two previous Fibonacci numbers. The current Fibonacci number would then be f0 + f1. The algorithm can be described as follows:
f0 = 0; // For fib(0)
f1 = 1; // For fib(1)
for (int i = 1; i <= n; i++) { currentFib = f0 + f1;
f0 = f1;
f1 = currentFib;
}
// After the loop, currentFib is fib(n)
Programming Exercises 701
20.3* (Computing greatest common divisor using recursion) The gcd(m, n) can also be defined recursively as follows:
■If m % n is 0, gcd (m, n) is n.
■Otherwise, gcd(m, n) is gcd(n, m % n).
Write a recursive method to find the GCD. Write a test program that computes gcd(24, 16) and gcd(255, 25).
20.4(Summing series) Write a recursive method to compute the following series:
m1i2 = 1 + 1 + 1 + Á + 1
2 |
3 |
i |
20.5(Summing series) Write a recursive method to compute the following series:
m1i2 = |
1 |
+ |
2 |
+ |
3 |
+ |
4 |
+ |
5 |
+ |
6 |
+ Á + |
i |
3 |
5 |
7 |
9 |
11 |
13 |
2i + 1 |
20.6* (Summing series) Write a recursive method to compute the following series:
m1i2 = |
1 |
+ |
2 |
+ Á + |
i |
2 |
3 |
i + 1 |
20.7* (Fibonacci series) Modify Listing 20.2, ComputeFibonacci.java, so that the program finds the number of times the fib method is called.
(Hint: Use a static variable and increment it every time the method is called.)
Section 20.4
20.8* (Printing the digits in an integer reversely) Write a recursive method that displays an int value reversely on the console using the following header:
public static void reverseDisplay(int value)
For example, reverseDisplay(12345) displays 54321.
20.9* (Printing the characters in a string reversely) Write a recursive method that displays a string reversely on the console using the following header:
public static void reverseDisplay(String value)
For example, reverseDisplay("abcd") displays dcba.
20.10* (Occurrences of a specified character in a string) Write a recursive method that finds the number of occurrences of a specified letter in a string using the following method header.
public static int count(String str, char a)
For example, count("Welcome", 'e') returns 2.
20.11* (Summing the digits in an integer using recursion) Write a recursive method that computes the sum of the digits in an integer. Use the following method header:
public static int sumDigits(long n)
For example, sumDigits(234) returns 2 + 3 + 4 = 9.

702 Chapter 20 Recursion
Section 20.5
20.12** (Printing the characters in a string reversely) Rewrite Exercise 20.9 using a helper method to pass the substring high index to the method. The helper method header is:
public static void reverseDisplay(String value, int high)
20.13* (Finding the largest number in an array) Write a recursive method that returns the largest integer in an array.
20.14* (Finding the number of uppercase letters in a string) Write a recursive method to return the number of uppercase letters in a string.
20.15* (Occurrences of a specified character in a string) Rewrite Exercise 20.10 using a helper method to pass the substring high index to the method. The helper method header is:
public static int count(String str, char a, int high)
20.16* (Finding the number of uppercase letters in an array) Write a recursive method to return the number of uppercase letters in an array of characters. You need to define the following two methods. The second one is a recursive helper method.
public static int count(char[] chars)
public static int count(char[] chars, int high)
20.17* (Occurrences of a specified character in an array) Write a recursive method that finds the number of occurrences of a specified character in an array. You need to define the following two methods. The second one is a recursive helper method.
public static int count(char[] chars, char ch)
public static int count(char[] chars, char ch, int high)
Sections 20.6
20.18* (Towers of Hanoi) Modify Listing 20.8, TowersOfHanoi.java, so that the program finds the number of moves needed to move n disks from tower A to tower B.
(Hint: Use a static variable and increment it every time the method is called.) 20.19* (Sierpinski triangle) Revise Listing 20.9 to develop an applet that lets the user
use the Increase and Decrease buttons to increase or decrease the current order by 1, as shown in Figure 20.13(a). The initial order is 0. If the current order is 0, the Decrease button is ignored.
(a) |
(b) |
FIGURE 20.13 (a) Exercise 20.19 uses the Increase and Decrease buttons to increase or decrease the current order by 1. (b) Exercise 20.20 draws ovals using a recursive method.
Programming Exercises 703
20.20* (Displaying circles) Write a Java applet that displays ovals, as shown in Figure 20.13(b). The ovals are centered in the panel. The gap between two adjacent ovals is 10 pixels, and the gap between the panel and the largest oval is also 10.
Comprehensive
20.21* (Decimal to binary) Write a recursive method that converts a decimal number into a binary number as a string. The method header is as follows:
public static String decimalToBinary(int value)
20.22* (Decimal to hex) Write a recursive method that converts a decimal number into a hex number as a string. The method header is as follows:
public static String decimalToHex(int value)
20.23* (Binary to decimal) Write a recursive method that parses a binary number as a string into a decimal integer. The method header is as follows:
public static int binaryToDecimal(String binaryString)
20.24* (Hex to decimal) Write a recursive method that parses a hex number as a string into a decimal integer. The method header is as follows:
public static int hexToDecimal(String hexString)
20.25** (String permutation) Write a recursive method to print all the permutations of a string. For example, for a string abc, the printout is
abc acb bac bca cab cba
(Hint: Define the following two methods. The second is a helper method.)
public static void displayPermuation(String s)
public static void displayPermuation(String s1, String s2)
The first method simply invokes displayPermuation("", s). The second method uses a loop to move a character from s2 to s1 and recursively invoke it with a new s1 and s2. The base case is that s2 is empty and prints s1 to the console.
20.26** (Creating a maze) Write an applet that will find a path in a maze, as shown in Figure 20.14(a). The maze is represented by an 8 * 8 board. The path must meet the following conditions:
■The path is between the upper-left corner cell and the lower-right corner cell in the maze.
■The applet enables the user to place or remove a mark on a cell. A path consists of adjacent unmarked cells. Two cells are said to be adjacent if they are horizontal or vertical neighbors, but not if they are diagonal neighbors.
■The path does not contain cells that form a square. The path in Figure 20.14(b), for example, does not meet this condition. (The condition makes a path easy to identify on the board.)

704 Chapter 20 Recursion
(a) Correct path |
(b) Illegal path |
FIGURE 20.14 The program finds a path from the upper-left corner to the bottom-right corner.
20.27** (Koch snowflake fractal) The text presented the Sierpinski triangle fractal. In this exercise, you will write an applet to display another fractal, called the Koch snowflake, named after a famous Swedish mathematician. A Koch snowflake is created as follows:
1.Begin with an equilateral triangle, which is considered to be the Koch fractal of order (or level) 0, as shown in Figure 20.15(a).
2.Divide each line in the shape into three equal line segments and draw an outward equilateral triangle with the middle line segment as the base to create a Koch fractal of order 1, as shown in Figure 20.15(b).
3.Repeat step 2 to create a Koch fractal of order 2, 3, Á , and so on, as shown in Figure 20.15(c–d).
(a) |
(b) |
(c) |
(d) |
FIGURE 20.15 A Koch snowflake is a fractal starting with a triangle.
Video Note
Search a string in a directory
20.28** (Nonrecursive directory size) Rewrite Listing 20.7, DirectorySize.java, without using recursion.
20.29* (Number of files in a directory) Write a program that prompts the user to enter a directory and displays the number of the files in the directory.
20.30** (Finding words) Write a program that finds all occurrences of a word in all the files under a directory, recursively. Pass the parameters from the command line as follows:
java Exercise20_30 dirName word
20.31** (Replacing words) Write a program that replaces all occurrences of a word with a new word in all the files under a directory, recursively. Pass the parameters from the command line as follows:
java Exercise20_31 dirName oldWord newWord
Programming Exercises 705
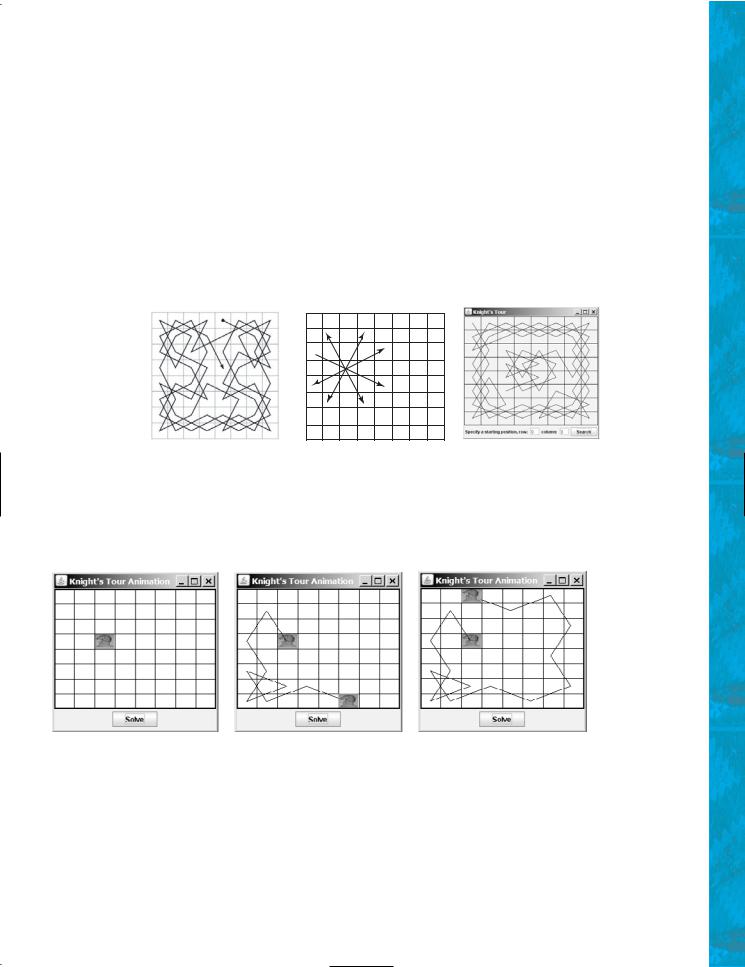
20.32*** (Game: Knight’s Tour) The Knight’s Tour is an ancient puzzle. The objective is to move a knight, starting from any square on a chessboard, to every other square once, as shown in Figure 20.16(a). Note that the knight makes only L-shape moves (two spaces in one direction and one space in a perpendicular direction). As shown in Figure 20.16(b), the knight can move to eight squares. Write a program that displays the moves for the knight in an applet, as shown in Figure 20.16(c).
(Hint: A brute-force approach for this problem is to move the knight from one square to another available square arbitrarily. Using such an approach, your program will take a long time to finish. A better approach is to employ some heuristics. A knight has two, three, four, six, or eight possible moves, depending on its location. Intuitively, you should attempt to move the knight to the least accessible squares first and leave those more accessible squares open, so there will be a better chance of success at the end of the search.)
0 1 2 3 4 5 6 7
0
1
2 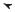
3
4
5
6
7
(a) |
(b) |
(c) |
FIGURE 20.16 (a) A knight traverses all squares once. (b) A knight makes an L-shape move. (c) An applet displays a knight tour path.
20.33*** (Game: Knight’s Tour animation) Write an applet for the Knight’s Tour problem. Your applet should let the user move a knight to any starting square and click the Solve button to animate a knight moving along the path, as shown in Figure 20.17.
FIGURE 20.17 A knight traverses along the path.
20.34** (Game: Sudoku) Write a program to solve the Sudoku problem using recursion. 20.35** (H-tree fractal) An H-tree is a fractal defined as follows:
1.Begin with a letter H. The three lines of the H are of the same length, as shown in Figure 20.18(a).
2.The letter H (in its sans-serif form, H) has four endpoints. Draw an H centered at each of the four endpoints to an H-tree of order 1, as shown in Figure 20.18(b). These H’s are half the size of the H that contains the four endpoints.
3.Repeat step 2 to create a H-tree of order 2, 3, Á , and so on, as shown in Figure 20.18(c–d).

706 Chapter 20 Recursion
(a) |
(b) |
(c) |
(d) |
FIGURE 20.18 An H-tree is a fractal starting with three lines of equal length in an H-shape.
The H-tree is used in VLSI design as a clock distribution network for routing timing signals to all parts of a chip with equal propagation delays. Write an applet that draws an H-tree, as shown in Figure 20.18.
20.36***(Game: all Sudoku solutions) Rewrite Exercise 20.34 to find all possible solutions to a Sudoku problem.
20.37*** (Game: multiple Eight Queens solution) Write an applet to display all possible solutions for the Eight Queens puzzle in a scroll pane, as shown in Figure 20.19. For each solution, put a label to denote the solution number.
Hint: Place all solution panels into one panel and place this one panel into a JScrollPane. The solution panel class should override the getPreferredSize() method to ensure that a solution panel is displayed properly. See Listing 15.3, FigurePanel.java, on how to override getPreferredSize().
FIGURE 20.19 All solutions are placed in a scroll pane.
20.38** (Recursive tree) Write an applet to display a recursive tree as shown in Figure 20.20. 20.39** (Dragging the tree) Revise Exercise 20.38 to move the tree to where the mouse
is dragged.
(a) |
(b) |
(c) |
(d) |
FIGURE 20.20 A recursive tree with the specified depth.
