
- •CONTENTS
- •1.1 Introduction
- •1.2 What Is a Computer?
- •1.3 Programs
- •1.4 Operating Systems
- •1.5 Java, World Wide Web, and Beyond
- •1.6 The Java Language Specification, API, JDK, and IDE
- •1.7 A Simple Java Program
- •1.8 Creating, Compiling, and Executing a Java Program
- •1.9 (GUI) Displaying Text in a Message Dialog Box
- •2.1 Introduction
- •2.2 Writing Simple Programs
- •2.3 Reading Input from the Console
- •2.4 Identifiers
- •2.5 Variables
- •2.7 Named Constants
- •2.8 Numeric Data Types and Operations
- •2.9 Problem: Displaying the Current Time
- •2.10 Shorthand Operators
- •2.11 Numeric Type Conversions
- •2.12 Problem: Computing Loan Payments
- •2.13 Character Data Type and Operations
- •2.14 Problem: Counting Monetary Units
- •2.15 The String Type
- •2.16 Programming Style and Documentation
- •2.17 Programming Errors
- •2.18 (GUI) Getting Input from Input Dialogs
- •3.1 Introduction
- •3.2 boolean Data Type
- •3.3 Problem: A Simple Math Learning Tool
- •3.4 if Statements
- •3.5 Problem: Guessing Birthdays
- •3.6 Two-Way if Statements
- •3.7 Nested if Statements
- •3.8 Common Errors in Selection Statements
- •3.9 Problem: An Improved Math Learning Tool
- •3.10 Problem: Computing Body Mass Index
- •3.11 Problem: Computing Taxes
- •3.12 Logical Operators
- •3.13 Problem: Determining Leap Year
- •3.14 Problem: Lottery
- •3.15 switch Statements
- •3.16 Conditional Expressions
- •3.17 Formatting Console Output
- •3.18 Operator Precedence and Associativity
- •3.19 (GUI) Confirmation Dialogs
- •4.1 Introduction
- •4.2 The while Loop
- •4.3 The do-while Loop
- •4.4 The for Loop
- •4.5 Which Loop to Use?
- •4.6 Nested Loops
- •4.7 Minimizing Numeric Errors
- •4.8 Case Studies
- •4.9 Keywords break and continue
- •4.10 (GUI) Controlling a Loop with a Confirmation Dialog
- •5.1 Introduction
- •5.2 Defining a Method
- •5.3 Calling a Method
- •5.4 void Method Example
- •5.5 Passing Parameters by Values
- •5.6 Modularizing Code
- •5.7 Problem: Converting Decimals to Hexadecimals
- •5.8 Overloading Methods
- •5.9 The Scope of Variables
- •5.10 The Math Class
- •5.11 Case Study: Generating Random Characters
- •5.12 Method Abstraction and Stepwise Refinement
- •6.1 Introduction
- •6.2 Array Basics
- •6.3 Problem: Lotto Numbers
- •6.4 Problem: Deck of Cards
- •6.5 Copying Arrays
- •6.6 Passing Arrays to Methods
- •6.7 Returning an Array from a Method
- •6.8 Variable-Length Argument Lists
- •6.9 Searching Arrays
- •6.10 Sorting Arrays
- •6.11 The Arrays Class
- •7.1 Introduction
- •7.2 Two-Dimensional Array Basics
- •7.3 Processing Two-Dimensional Arrays
- •7.4 Passing Two-Dimensional Arrays to Methods
- •7.5 Problem: Grading a Multiple-Choice Test
- •7.6 Problem: Finding a Closest Pair
- •7.7 Problem: Sudoku
- •7.8 Multidimensional Arrays
- •8.1 Introduction
- •8.2 Defining Classes for Objects
- •8.3 Example: Defining Classes and Creating Objects
- •8.4 Constructing Objects Using Constructors
- •8.5 Accessing Objects via Reference Variables
- •8.6 Using Classes from the Java Library
- •8.7 Static Variables, Constants, and Methods
- •8.8 Visibility Modifiers
- •8.9 Data Field Encapsulation
- •8.10 Passing Objects to Methods
- •8.11 Array of Objects
- •9.1 Introduction
- •9.2 The String Class
- •9.3 The Character Class
- •9.4 The StringBuilder/StringBuffer Class
- •9.5 Command-Line Arguments
- •9.6 The File Class
- •9.7 File Input and Output
- •9.8 (GUI) File Dialogs
- •10.1 Introduction
- •10.2 Immutable Objects and Classes
- •10.3 The Scope of Variables
- •10.4 The this Reference
- •10.5 Class Abstraction and Encapsulation
- •10.6 Object-Oriented Thinking
- •10.7 Object Composition
- •10.8 Designing the Course Class
- •10.9 Designing a Class for Stacks
- •10.10 Designing the GuessDate Class
- •10.11 Class Design Guidelines
- •11.1 Introduction
- •11.2 Superclasses and Subclasses
- •11.3 Using the super Keyword
- •11.4 Overriding Methods
- •11.5 Overriding vs. Overloading
- •11.6 The Object Class and Its toString() Method
- •11.7 Polymorphism
- •11.8 Dynamic Binding
- •11.9 Casting Objects and the instanceof Operator
- •11.11 The ArrayList Class
- •11.12 A Custom Stack Class
- •11.13 The protected Data and Methods
- •11.14 Preventing Extending and Overriding
- •12.1 Introduction
- •12.2 Swing vs. AWT
- •12.3 The Java GUI API
- •12.4 Frames
- •12.5 Layout Managers
- •12.6 Using Panels as Subcontainers
- •12.7 The Color Class
- •12.8 The Font Class
- •12.9 Common Features of Swing GUI Components
- •12.10 Image Icons
- •13.1 Introduction
- •13.2 Exception-Handling Overview
- •13.3 Exception-Handling Advantages
- •13.4 Exception Types
- •13.5 More on Exception Handling
- •13.6 The finally Clause
- •13.7 When to Use Exceptions
- •13.8 Rethrowing Exceptions
- •13.9 Chained Exceptions
- •13.10 Creating Custom Exception Classes
- •14.1 Introduction
- •14.2 Abstract Classes
- •14.3 Example: Calendar and GregorianCalendar
- •14.4 Interfaces
- •14.5 Example: The Comparable Interface
- •14.6 Example: The ActionListener Interface
- •14.7 Example: The Cloneable Interface
- •14.8 Interfaces vs. Abstract Classes
- •14.9 Processing Primitive Data Type Values as Objects
- •14.10 Sorting an Array of Objects
- •14.11 Automatic Conversion between Primitive Types and Wrapper Class Types
- •14.12 The BigInteger and BigDecimal Classes
- •14.13 Case Study: The Rational Class
- •15.1 Introduction
- •15.2 Graphical Coordinate Systems
- •15.3 The Graphics Class
- •15.4 Drawing Strings, Lines, Rectangles, and Ovals
- •15.5 Case Study: The FigurePanel Class
- •15.6 Drawing Arcs
- •15.7 Drawing Polygons and Polylines
- •15.8 Centering a String Using the FontMetrics Class
- •15.9 Case Study: The MessagePanel Class
- •15.10 Case Study: The StillClock Class
- •15.11 Displaying Images
- •15.12 Case Study: The ImageViewer Class
- •16.1 Introduction
- •16.2 Event and Event Source
- •16.3 Listeners, Registrations, and Handling Events
- •16.4 Inner Classes
- •16.5 Anonymous Class Listeners
- •16.6 Alternative Ways of Defining Listener Classes
- •16.7 Problem: Loan Calculator
- •16.8 Window Events
- •16.9 Listener Interface Adapters
- •16.10 Mouse Events
- •16.11 Key Events
- •16.12 Animation Using the Timer Class
- •17.1 Introduction
- •17.2 Buttons
- •17.3 Check Boxes
- •17.4 Radio Buttons
- •17.5 Labels
- •17.6 Text Fields
- •17.7 Text Areas
- •17.8 Combo Boxes
- •17.9 Lists
- •17.10 Scroll Bars
- •17.11 Sliders
- •17.12 Creating Multiple Windows
- •18.1 Introduction
- •18.2 Developing Applets
- •18.3 The HTML File and the <applet> Tag
- •18.4 Applet Security Restrictions
- •18.5 Enabling Applets to Run as Applications
- •18.6 Applet Life-Cycle Methods
- •18.7 Passing Strings to Applets
- •18.8 Case Study: Bouncing Ball
- •18.9 Case Study: TicTacToe
- •18.10 Locating Resources Using the URL Class
- •18.11 Playing Audio in Any Java Program
- •18.12 Case Study: Multimedia Animations
- •19.1 Introduction
- •19.2 How is I/O Handled in Java?
- •19.3 Text I/O vs. Binary I/O
- •19.4 Binary I/O Classes
- •19.5 Problem: Copying Files
- •19.6 Object I/O
- •19.7 Random-Access Files
- •20.1 Introduction
- •20.2 Problem: Computing Factorials
- •20.3 Problem: Computing Fibonacci Numbers
- •20.4 Problem Solving Using Recursion
- •20.5 Recursive Helper Methods
- •20.6 Problem: Finding the Directory Size
- •20.7 Problem: Towers of Hanoi
- •20.8 Problem: Fractals
- •20.9 Problem: Eight Queens
- •20.10 Recursion vs. Iteration
- •20.11 Tail Recursion
- •APPENDIXES
- •INDEX
692 Chapter 20 Recursion
Video Note
Fractal (Sierpinski triangle)
20.8 Problem: Fractals
A fractal is a geometrical figure, but unlike triangles, circles, and rectangles, fractals can be divided into parts, each a reduced-size copy of the whole. There are many interesting examples of fractals. This section introduces a simple fractal, the Sierpinski triangle, named after a famous Polish mathematician.
A Sierpinski triangle is created as follows:
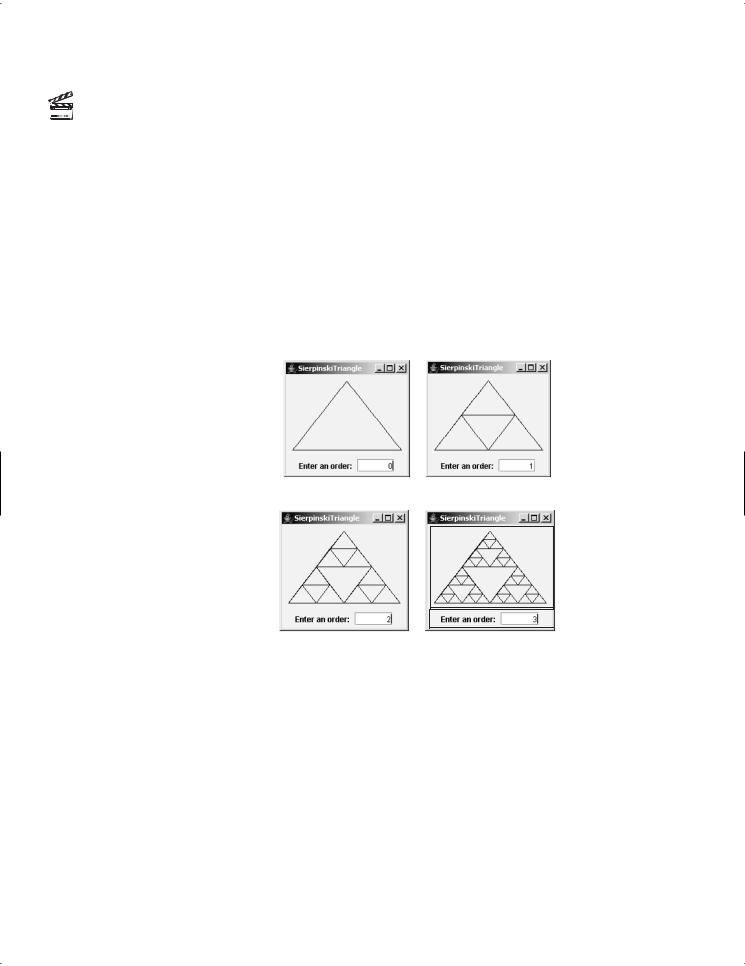
1.Begin with an equilateral triangle, which is considered to be a Sierpinski fractal of order (or level) 0, as shown in Figure 20.9(a).
2.Connect the midpoints of the sides of the triangle of order 0 to create a Sierpinski triangle of order 1 (Figure 20.9(b)).
3.Leave the center triangle intact. Connect the midpoints of the sides of the three other triangles to create a Sierpinski triangle of order 2 (Figure 20.9(c)).
4.You can repeat the same process recursively to create a Sierpinski triangle of order 3, 4,
Á, and so on (Figure 20.9(d)).
(a) Order 0 |
(b) Order 1 |
 JPanel
JPanel

 JPanel
JPanel
(c) Order 2 |
(d) Order 3 |
FIGURE 20.9 A Sierpinski triangle is a pattern of recursive triangles.
The problem is inherently recursive. How do you develop a recursive solution for it? Consider the base case when the order is 0. It is easy to draw a Sierpinski triangle of order 0. How do you draw a Sierpinski triangle of order 1? The problem can be reduced to drawing three Sierpinski triangles of order 0. How do you draw a Sierpinski triangle of order 2? The problem can be reduced to drawing three Sierpinski triangles of order 1. So the problem of drawing a Sierpinski triangle of order n can be reduced to drawing three Sierpinski triangles of order n - 1.
Listing 20.9 gives a Java applet that displays a Sierpinski triangle of any order, as shown in Figure 20.9. You can enter an order in a text field to display a Sierpinski triangle of the specified order.
LISTING 20.9 SierpinskiTriangle.java
1 import javax.swing.*;
2 import java.awt.*;
3 import java.awt.event.*;

20.8 Problem: Fractals 693
4
5 public class SierpinskiTriangle extends JApplet {
6 private JTextField jtfOrder = new JTextField("0", 5); // Order
7private SierpinskiTrianglePanel trianglePanel =
8 new SierpinskiTrianglePanel(); // To display the pattern
9
10public SierpinskiTriangle() {
11// Panel to hold label, text field, and a button
12JPanel panel = new JPanel();
13panel.add(new JLabel("Enter an order: "));
14panel.add(jtfOrder);
15jtfOrder.setHorizontalAlignment(SwingConstants.RIGHT);
17// Add a Sierpinski triangle panel to the applet
18add(trianglePanel);
19add(panel, BorderLayout.SOUTH);
21// Register a listener
22 |
jtfOrder.addActionListener(new ActionListener() { |
|
listener |
23 |
public void actionPerformed(ActionEvent e) { |
|
|
24 |
trianglePanel.setOrder(Integer.parseInt(jtfOrder.getText())); |
set a new order |
|
25}
26});
27}
28
29static class SierpinskiTrianglePanel extends JPanel {
30private int order = 0;
31
32/** Set a new order */
33public void setOrder(int order) {
34this.order = order;
35repaint();
36}
37
38protected void paintComponent(Graphics g) {
39super.paintComponent(g);
40 |
|
|
|
|
41 |
// Select three points in proportion to the panel size |
|
||
42 |
|
Point p1 = new Point(getWidth() / 2, 10); |
|
three initial points |
43Point p2 = new Point(10, getHeight() - 10);
44Point p3 = new Point(getWidth() - 10, getHeight() - 10);
46displayTriangles(g, order, p1, p2, p3);
47 |
} |
48 |
|
49private static void displayTriangles(Graphics g, int order,
50Point p1, Point p2, Point p3) {
51if (order >= 0) {
52// Draw a triangle to connect three points
53 |
g.drawLine(p1.x, p1.y, p2.x, p2.y); |
draw a triangle |
54g.drawLine(p1.x, p1.y, p3.x, p3.y);
55g.drawLine(p2.x, p2.y, p3.x, p3.y);
57// Get the midpoint on each edge in the triangle
58Point p12 = midpoint(p1, p2);
59Point p23 = midpoint(p2, p3);
60Point p31 = midpoint(p3, p1);
62// Recursively display three triangles
63 |
displayTriangles(g, order - 1, p1, p12, p31); |
top subtriangle |
694 Chapter 20 |
Recursion |
|||||
|
|
|
|
|
||
left subtriangle |
64 |
|
|
displayTriangles(g, order - 1, p12, p2, p23); |
|
|
right subtriangle |
65 |
|
|
displayTriangles(g, order - 1, p31, p23, p3); |
|
|
|
66 |
|
} |
|
|
|
|
67 |
|
} |
|
|
|
|
68 |
|
|
|
|
|
|
69 |
|
private static Point midpoint(Point p1, Point p2) { |
|||
|
70 |
|
return new Point((p1.x + p2.x) / 2, (p1.y + p2.y) / 2); |
|||
|
71 |
|
} |
|
|
|
|
72 |
|
} |
|
|
|
main method omitted |
73 |
} |
|
|
|
|
The initial triangle has three points set in proportion to the panel size (lines 42–44). The displayTriangles(g, order, p1, p2, p3) method (lines 49–67) performs the following tasks if order >= 0:
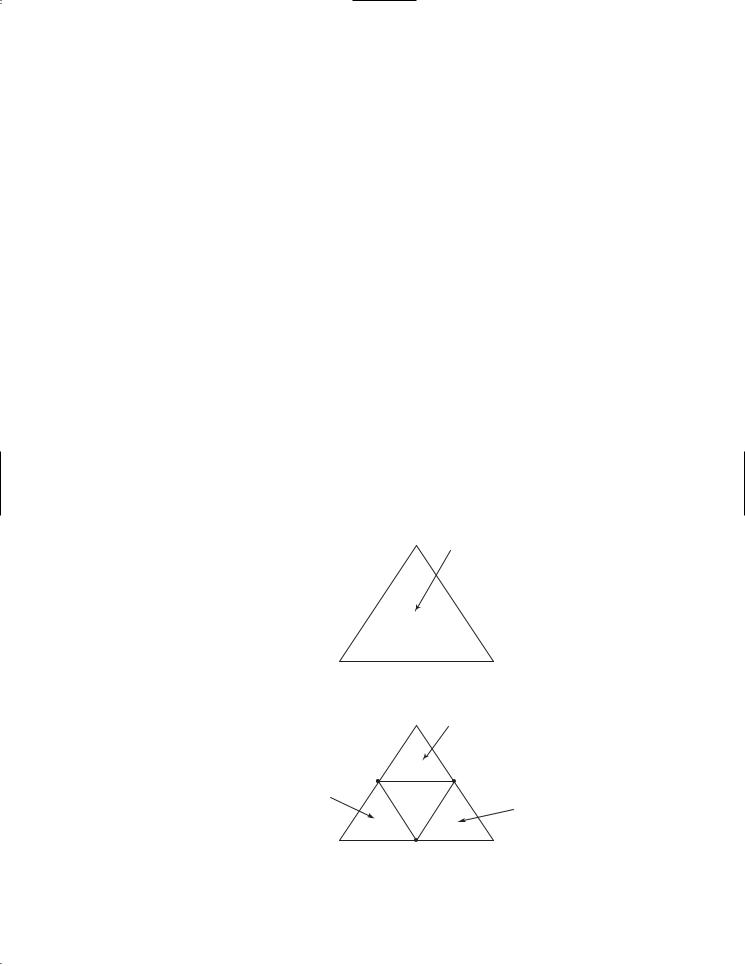
1.Display a triangle to connect three points p1, p2, and p3 in lines 53–55 , as shown in Figure 20.10(a).
2.Obtain a midpoint between p1 and p2 (line 58), a midpoint between p2 and p3 (line 59), and a midpoint between p3 and p1 (line 60), as shown in Figure 20.10(b).
3.Recursively invoke displayTriangles with a reduced order to display three smaller Sierpinski triangles (lines 63–66). Note each small Sierpinski triangle is structurally identical to the original big Sierpinski triangle except that the order of a small triangle is one less, as shown in Figure 20.10(b).
A Sierpinski triangle is displayed in a SierpinskiTrianglePanel. The order property in the inner class SierpinskiTrianglePanel specifies the order for the Sierpinski triangle. The Point class, introduced in §16.10, “Mouse Events,” represents a point on a component. The midpoint(Point p1, Point p2) method returns the midpoint between p1 and p2 (lines 72–74).
p1 Draw the Sierpinski triangle displayTriangles(g, order, p1, p2, p3)
p2
(a)
p1
p3
Recursively draw the small Sierpinski triangle displayTriangles(g,
order - 1, p1, p12, p31)
Recursively draw the small |
p12 |
p31 |
|
|
|
Sierpinski triangle |
|
|
displayTriangles(g, |
|
|
order - 1, p12, p2, p23) |
|
|
p2 |
p3 |
p23
(b)
Recursively draw the small Sierpinski triangle displayTriangles(g,
order - 1, p31, p23, p3)
FIGURE 20.10 Drawing a Sierpinski triangle spawns calls to draw three small Sierpinski triangles recursively.
20.9 Problem: Eight Queens 695
20.9 Problem: Eight Queens
This section gives a recursive solution to the Eight Queens problem presented at the beginning of the chapter. The task is to find a solution to place a queen in each row on a chessboard such that no two queens can attack each other. You may use a two-dimensional array to represent a chessboard. However, since each row can have only one queen, it is sufficient to use a one-dimensional array to denote the position of the queen in the row. So, you may define array queens as follows:
int[] queens = new int[8];
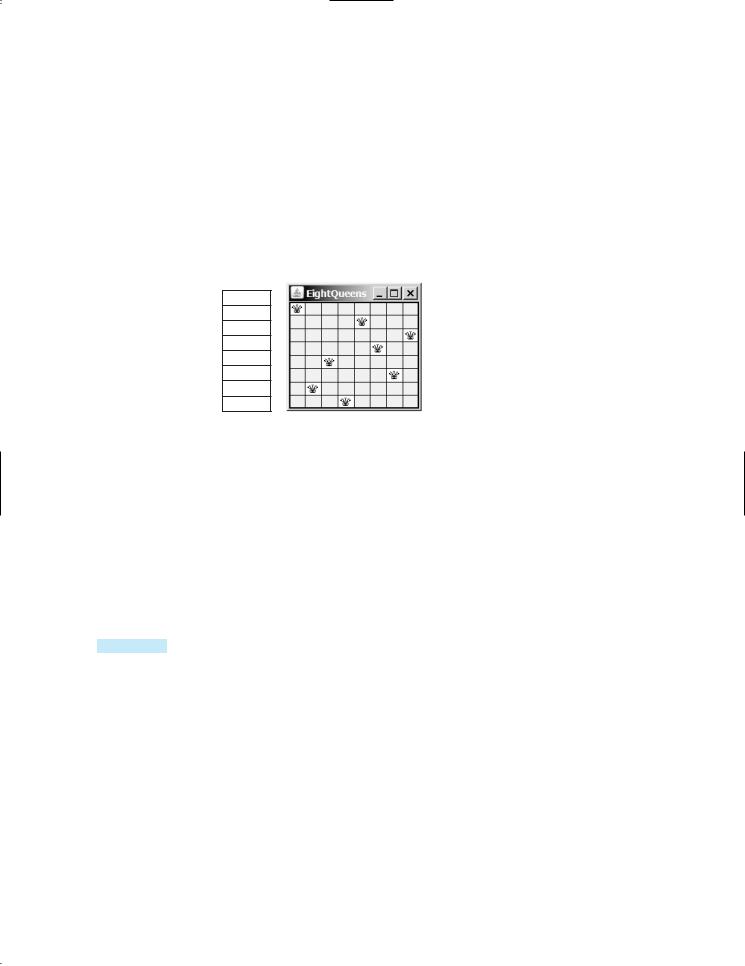
Assign j to queens[i] to denote that a queen is placed in row i and column j. Figure 20.11(a) shows the contents of array queens for the chessboard in Figure 20.11(b).
queens[0] 0 queens[1] 4 queens[2] 7 queens[3] 5 queens[4] 2 queens[5] 6 queens[6] 1 queens[7] 3
(a) |
(b) |
FIGURE 20.11 queens[i] denotes the position of the queen in row i.
Listing 20.10 gives the program that displays a solution for the Eight Queens problem.
LISTING 20.10 EightQueens.java
1 import java.awt.*;
2 import javax.swing.*;
3
4 public class EightQueens extends JApplet {
5 public static final int SIZE = 8; // The size of the chessboard 6 private int[] queens = new int[SIZE]; // Queen positions
7
8public EightQueens() {
9 |
search(0); // Search for a solution from row 0 |
search for solution |
10add(new ChessBoard(), BorderLayout.CENTER); // Display solution
11}
12 |
|
|
|
|
|
13 |
/** Check if a queen can be |
placed at row i and column j */ |
|
||
14 |
|
private boolean isValid(int |
row, int column) { |
|
check whether valid |
15for (int i = 1; i <= row; i++)
16if (queens[row - i] == column // Check column
17|| queens[row - i] == column - i // Check upleft diagonal
18|| queens[row - i] == column + i) // Check upright diagonal
19return false; // There is a conflict
20return true; // No conflict
21}
22 |
|
|
|
|
23 |
/** Search for a solution starting from a specified row */ |
|
||
24 |
|
private boolean search(int row) { |
|
search this row |
25 |
|
if (row == SIZE) // Stopping condition |
|
|
26 |
|
return true; // A solution found to place 8 queens in 8 rows |
search columns |
|
27 |
|
|
|
|
28 |
|
for (int column = 0; column < SIZE; column++) { |
search next row |
|

696 Chapter 20 Recursion
|
29 |
|
queens[row] = column; // Place a queen at (row, column) |
||
|
30 |
|
if (isValid(row, column) && |
search(row + 1) |
) |
found |
31 |
|
return true; // Found, thus return true to exit for loop |
||
|
32 |
|
} |
|
|
|
33 |
|
|
|
|
|
34 |
|
// No solution for a queen placed at any column of this row |
||
|
35 |
|
return false; |
||
|
36 |
|
} |
|
|
|
37 |
|
|
|
|
|
38 |
|
class ChessBoard extends JPanel { |
||
|
39 |
|
private Image queenImage = |
||
|
40 |
|
new ImageIcon("image/queen.jpg").getImage(); |
||
|
41 |
|
|
|
|
|
42 |
|
ChessBoard() { |
||
|
43 |
|
this.setBorder(BorderFactory.createLineBorder(Color.BLACK, 2)); |
||
|
44 |
|
} |
|
|
|
45 |
|
|
|
|
|
46 |
|
protected void paintComponent(Graphics g) { |
||
|
47 |
|
super.paintComponent(g); |
||
|
48 |
|
|
|
|
|
49 |
|
// Paint the queens |
||
|
50 |
|
for (int i = 0; i < SIZE; i++) { |
||
|
51 |
|
int j = queens[i]; // The position of the queen in row i |
||
|
52 |
|
g.drawImage(queenImage, j * getWidth() / SIZE, |
||
|
53 |
|
i * getHeight() / SIZE, getWidth() / SIZE, |
||
|
54 |
|
getHeight() / SIZE, this); |
||
|
55 |
|
} |
|
|
|
56 |
|
|
|
|
|
57 |
|
// Draw the horizontal and vertical lines |
||
|
58 |
|
for (int i = 1; i < SIZE; i++) { |
||
|
59 |
|
g.drawLine(0, i * getHeight() / SIZE, |
||
|
60 |
|
getWidth(), i * getHeight() / SIZE); |
||
|
61 |
|
g.drawLine(i * getWidth() / SIZE, 0, |
||
|
62 |
|
i * getWidth() / SIZE, getHeight()); |
||
|
63 |
|
} |
|
|
|
64 |
|
} |
|
|
|
65 |
|
} |
|
|
main method omitted |
66 |
} |
|
|
|
The program invokes search(0) (line 9) to start a search for a solution at row 0, which recursively invokes search(1), search(2), Á , and search(7) (line 30).
The recursive search(row) method returns true if all row are filled (lines 25–26). The method checks whether a queen can be placed in column 0, 1, 2, Á , and 7 in a for loop (line 28). Place a queen in the column (line 29). If the placement is valid, recursively search for the next row by invoking search(row + 1) (line 30). If search is successful, return true (line 31) to exit the for loop. In this case, there is no need to look for the next column in the row. If there is no solution for a queen to be placed on any column of this row, the method returns false (line 35).
Suppose you invoke search(row) for row 3, as shown in Figure 20.12(a). The method tries to fill in a queen in column 0, 1, 2, and so on in this order. For each trial, the isValid(row, column) method (line 30) is called to check whether placing a queen at the specified position causes a conflict with the queens placed earlier. It ensures that no queen is placed in the same column (line 16), no queen is placed in the upper left diagonal (line 17), and no queen is placed in the upper right diagonal (line 18), as shown in Figure 20.12(a). If isValid(row, column) returns false, check the next column, as shown Figure 20.12(b). If isValid(row, column) returns true, recursively invoke search(row + 1), as shown in Figure 20.12(d). If search(row + 1) returns false, check the next column on the preceding row, as shown Figure 20.12(c).
