
- •CONTENTS
- •1.1 Introduction
- •1.2 What Is a Computer?
- •1.3 Programs
- •1.4 Operating Systems
- •1.5 Java, World Wide Web, and Beyond
- •1.6 The Java Language Specification, API, JDK, and IDE
- •1.7 A Simple Java Program
- •1.8 Creating, Compiling, and Executing a Java Program
- •1.9 (GUI) Displaying Text in a Message Dialog Box
- •2.1 Introduction
- •2.2 Writing Simple Programs
- •2.3 Reading Input from the Console
- •2.4 Identifiers
- •2.5 Variables
- •2.7 Named Constants
- •2.8 Numeric Data Types and Operations
- •2.9 Problem: Displaying the Current Time
- •2.10 Shorthand Operators
- •2.11 Numeric Type Conversions
- •2.12 Problem: Computing Loan Payments
- •2.13 Character Data Type and Operations
- •2.14 Problem: Counting Monetary Units
- •2.15 The String Type
- •2.16 Programming Style and Documentation
- •2.17 Programming Errors
- •2.18 (GUI) Getting Input from Input Dialogs
- •3.1 Introduction
- •3.2 boolean Data Type
- •3.3 Problem: A Simple Math Learning Tool
- •3.4 if Statements
- •3.5 Problem: Guessing Birthdays
- •3.6 Two-Way if Statements
- •3.7 Nested if Statements
- •3.8 Common Errors in Selection Statements
- •3.9 Problem: An Improved Math Learning Tool
- •3.10 Problem: Computing Body Mass Index
- •3.11 Problem: Computing Taxes
- •3.12 Logical Operators
- •3.13 Problem: Determining Leap Year
- •3.14 Problem: Lottery
- •3.15 switch Statements
- •3.16 Conditional Expressions
- •3.17 Formatting Console Output
- •3.18 Operator Precedence and Associativity
- •3.19 (GUI) Confirmation Dialogs
- •4.1 Introduction
- •4.2 The while Loop
- •4.3 The do-while Loop
- •4.4 The for Loop
- •4.5 Which Loop to Use?
- •4.6 Nested Loops
- •4.7 Minimizing Numeric Errors
- •4.8 Case Studies
- •4.9 Keywords break and continue
- •4.10 (GUI) Controlling a Loop with a Confirmation Dialog
- •5.1 Introduction
- •5.2 Defining a Method
- •5.3 Calling a Method
- •5.4 void Method Example
- •5.5 Passing Parameters by Values
- •5.6 Modularizing Code
- •5.7 Problem: Converting Decimals to Hexadecimals
- •5.8 Overloading Methods
- •5.9 The Scope of Variables
- •5.10 The Math Class
- •5.11 Case Study: Generating Random Characters
- •5.12 Method Abstraction and Stepwise Refinement
- •6.1 Introduction
- •6.2 Array Basics
- •6.3 Problem: Lotto Numbers
- •6.4 Problem: Deck of Cards
- •6.5 Copying Arrays
- •6.6 Passing Arrays to Methods
- •6.7 Returning an Array from a Method
- •6.8 Variable-Length Argument Lists
- •6.9 Searching Arrays
- •6.10 Sorting Arrays
- •6.11 The Arrays Class
- •7.1 Introduction
- •7.2 Two-Dimensional Array Basics
- •7.3 Processing Two-Dimensional Arrays
- •7.4 Passing Two-Dimensional Arrays to Methods
- •7.5 Problem: Grading a Multiple-Choice Test
- •7.6 Problem: Finding a Closest Pair
- •7.7 Problem: Sudoku
- •7.8 Multidimensional Arrays
- •8.1 Introduction
- •8.2 Defining Classes for Objects
- •8.3 Example: Defining Classes and Creating Objects
- •8.4 Constructing Objects Using Constructors
- •8.5 Accessing Objects via Reference Variables
- •8.6 Using Classes from the Java Library
- •8.7 Static Variables, Constants, and Methods
- •8.8 Visibility Modifiers
- •8.9 Data Field Encapsulation
- •8.10 Passing Objects to Methods
- •8.11 Array of Objects
- •9.1 Introduction
- •9.2 The String Class
- •9.3 The Character Class
- •9.4 The StringBuilder/StringBuffer Class
- •9.5 Command-Line Arguments
- •9.6 The File Class
- •9.7 File Input and Output
- •9.8 (GUI) File Dialogs
- •10.1 Introduction
- •10.2 Immutable Objects and Classes
- •10.3 The Scope of Variables
- •10.4 The this Reference
- •10.5 Class Abstraction and Encapsulation
- •10.6 Object-Oriented Thinking
- •10.7 Object Composition
- •10.8 Designing the Course Class
- •10.9 Designing a Class for Stacks
- •10.10 Designing the GuessDate Class
- •10.11 Class Design Guidelines
- •11.1 Introduction
- •11.2 Superclasses and Subclasses
- •11.3 Using the super Keyword
- •11.4 Overriding Methods
- •11.5 Overriding vs. Overloading
- •11.6 The Object Class and Its toString() Method
- •11.7 Polymorphism
- •11.8 Dynamic Binding
- •11.9 Casting Objects and the instanceof Operator
- •11.11 The ArrayList Class
- •11.12 A Custom Stack Class
- •11.13 The protected Data and Methods
- •11.14 Preventing Extending and Overriding
- •12.1 Introduction
- •12.2 Swing vs. AWT
- •12.3 The Java GUI API
- •12.4 Frames
- •12.5 Layout Managers
- •12.6 Using Panels as Subcontainers
- •12.7 The Color Class
- •12.8 The Font Class
- •12.9 Common Features of Swing GUI Components
- •12.10 Image Icons
- •13.1 Introduction
- •13.2 Exception-Handling Overview
- •13.3 Exception-Handling Advantages
- •13.4 Exception Types
- •13.5 More on Exception Handling
- •13.6 The finally Clause
- •13.7 When to Use Exceptions
- •13.8 Rethrowing Exceptions
- •13.9 Chained Exceptions
- •13.10 Creating Custom Exception Classes
- •14.1 Introduction
- •14.2 Abstract Classes
- •14.3 Example: Calendar and GregorianCalendar
- •14.4 Interfaces
- •14.5 Example: The Comparable Interface
- •14.6 Example: The ActionListener Interface
- •14.7 Example: The Cloneable Interface
- •14.8 Interfaces vs. Abstract Classes
- •14.9 Processing Primitive Data Type Values as Objects
- •14.10 Sorting an Array of Objects
- •14.11 Automatic Conversion between Primitive Types and Wrapper Class Types
- •14.12 The BigInteger and BigDecimal Classes
- •14.13 Case Study: The Rational Class
- •15.1 Introduction
- •15.2 Graphical Coordinate Systems
- •15.3 The Graphics Class
- •15.4 Drawing Strings, Lines, Rectangles, and Ovals
- •15.5 Case Study: The FigurePanel Class
- •15.6 Drawing Arcs
- •15.7 Drawing Polygons and Polylines
- •15.8 Centering a String Using the FontMetrics Class
- •15.9 Case Study: The MessagePanel Class
- •15.10 Case Study: The StillClock Class
- •15.11 Displaying Images
- •15.12 Case Study: The ImageViewer Class
- •16.1 Introduction
- •16.2 Event and Event Source
- •16.3 Listeners, Registrations, and Handling Events
- •16.4 Inner Classes
- •16.5 Anonymous Class Listeners
- •16.6 Alternative Ways of Defining Listener Classes
- •16.7 Problem: Loan Calculator
- •16.8 Window Events
- •16.9 Listener Interface Adapters
- •16.10 Mouse Events
- •16.11 Key Events
- •16.12 Animation Using the Timer Class
- •17.1 Introduction
- •17.2 Buttons
- •17.3 Check Boxes
- •17.4 Radio Buttons
- •17.5 Labels
- •17.6 Text Fields
- •17.7 Text Areas
- •17.8 Combo Boxes
- •17.9 Lists
- •17.10 Scroll Bars
- •17.11 Sliders
- •17.12 Creating Multiple Windows
- •18.1 Introduction
- •18.2 Developing Applets
- •18.3 The HTML File and the <applet> Tag
- •18.4 Applet Security Restrictions
- •18.5 Enabling Applets to Run as Applications
- •18.6 Applet Life-Cycle Methods
- •18.7 Passing Strings to Applets
- •18.8 Case Study: Bouncing Ball
- •18.9 Case Study: TicTacToe
- •18.10 Locating Resources Using the URL Class
- •18.11 Playing Audio in Any Java Program
- •18.12 Case Study: Multimedia Animations
- •19.1 Introduction
- •19.2 How is I/O Handled in Java?
- •19.3 Text I/O vs. Binary I/O
- •19.4 Binary I/O Classes
- •19.5 Problem: Copying Files
- •19.6 Object I/O
- •19.7 Random-Access Files
- •20.1 Introduction
- •20.2 Problem: Computing Factorials
- •20.3 Problem: Computing Fibonacci Numbers
- •20.4 Problem Solving Using Recursion
- •20.5 Recursive Helper Methods
- •20.6 Problem: Finding the Directory Size
- •20.7 Problem: Towers of Hanoi
- •20.8 Problem: Fractals
- •20.9 Problem: Eight Queens
- •20.10 Recursion vs. Iteration
- •20.11 Tail Recursion
- •APPENDIXES
- •INDEX
678 Chapter 20 Recursion
|
20.1 Introduction |
search word problem |
Suppose you want to find all the files under a directory that contain a particular word. How do |
|
you solve this problem? There are several ways to do so. An intuitive and effective solution is |
|
to use recursion by searching the files in the subdirectories recursively. |
Eight Queens problem |
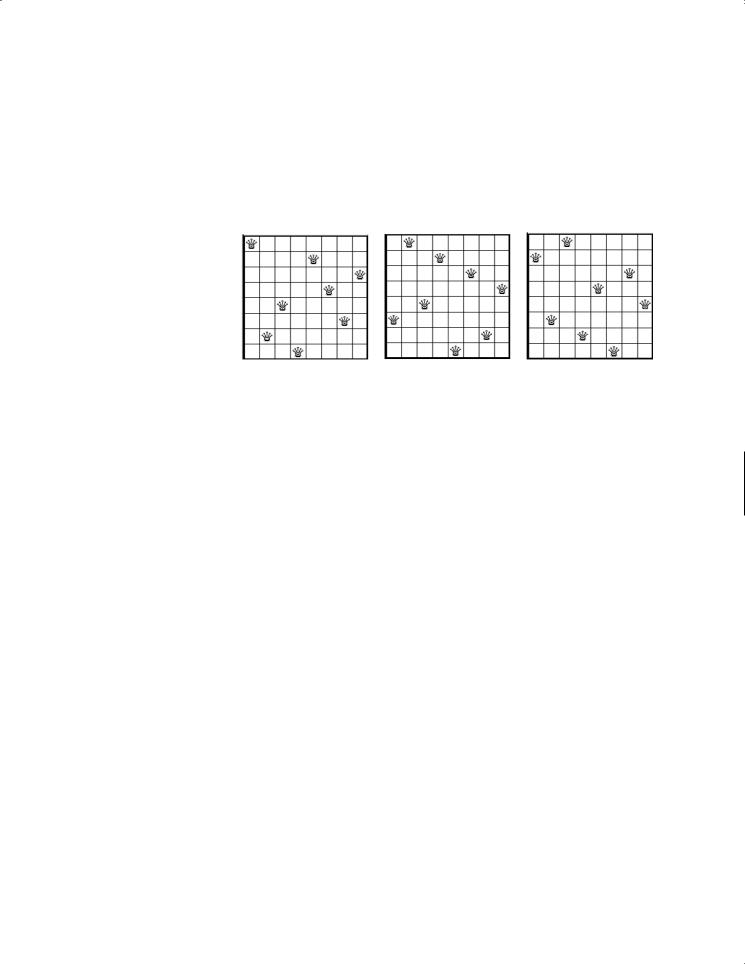
The classic Eight Queens puzzle is to place eight queens on a chessboard such that no two |
|
can attack each other (i.e., no two queens are on the same row, same column, or same diago- |
|
nal), as shown in Figure 20.1. How do you write a program to solve this problem? A good |
|
approach is to use recursion. |
|
FIGURE 20.1 The Eight Queens problem can be solved using recursion. |
recursive method |
To use recursion is to program using recursive methods—methods that directly or indi- |
|
rectly invoke themselves. Recursion is a useful programming technique. In some cases, it |
|
enables you to develop a natural, straightforward, simple solution to an otherwise difficult |
|
problem. This chapter introduces the concepts and techniques of recursive programming and |
|
illustrates by examples how to “think recursively.” |
base case or stopping condition
recursive call
20.2 Problem: Computing Factorials
Many mathematical functions are defined using recursion. We begin with a simple example. The factorial of a number n can be recursively defined as follows:
0! = 1;
n! = n × (n – 1) × ... × 2 × 1 = n × (n - 1)!; n > 0
How do you find n! for a given n? To find 1! is easy, because you know that 0! is 1, and 1! is 1 × 0!. Assuming that you know (n - 1)!, you can obtain n! immediately using n × (n - 1)!. Thus, the problem of computing n! is reduced to computing (n - 1)!. When computing (n - 1)!, you can apply the same idea recursively until n is reduced to 0.
Let factorial(n) be the method for computing n!. If you call the method with n = 0, it immediately returns the result. The method knows how to solve the simplest case, which is referred to as the base case or the stopping condition. If you call the method with n > 0, it reduces the problem into a subproblem for computing the factorial of n - 1. The subproblem is essentially the same as the original problem, but is simpler or smaller. Because the subproblem has the same property as the original, you can call the method with a different argument, which is referred to as a recursive call.
The recursive algorithm for computing factorial(n) can be simply described as follows:
if (n == 0) return 1;
else
return n * factorial(n - 1);
A recursive call can result in many more recursive calls, because the method keeps on dividing a subproblem into new subproblems. For a recursive method to terminate, the problem
20.2 Problem: Computing Factorials 679
must eventually be reduced to a stopping case, at which point the method returns a result to its caller. The caller then performs a computation and returns the result to its own caller. This process continues until the result is passed back to the original caller. The original problem can now be solved by multiplying n by the result of factorial(n - 1).
Listing 20.1 gives a complete program that prompts the user to enter a nonnegative integer and displays the factorial for the number.
LISTING 20.1 ComputeFactorial.java
1 import java.util.Scanner;
2
3 public class ComputeFactorial {
4/** Main method */
5 public static void main(String[] args) {
6// Create a Scanner
7Scanner input = new Scanner(System.in);
8 System.out.print("Enter a nonnegative integer: ");
9 int n = input.nextInt();
10
11// Display factorial
12System.out.println("Factorial of " + n + " is " + factorial(n));
13}
14
15/** Return the factorial for a specified number */
16public static long factorial(int n) {
17 |
if (n == 0) // Base case |
base case |
18return 1;
19else
20 |
return n * factorial(n - 1); // Recursive call |
recursion |
21}
22}
Enter a nonnegative integer: 4
Factorial of 4 is 24
Enter a nonnegative integer: 10
Factorial of 10 is 3628800
The factorial method (lines 16–21) is essentially a direct translation of the recursive mathematical definition for the factorial into Java code. The call to factorial is recursive because it calls itself. The parameter passed to factorial is decremented until it reaches the base case of 0.
Figure 20.2 illustrates the execution of the recursive calls, starting with n = 4. The use of stack space for recursive calls is shown in Figure 20.3.
Caution
If recursion does not reduce the problem in a manner that allows it to eventually converge into
the base case, infinite recursion can occur. For example, suppose you mistakenly write the infinite recursion factorial method as follows:
public static long factorial(int n) {
return n * factorial(n - 1);
}
The method runs infinitely and causes a StackOverflowError.
680 Chapter 20 Recursion
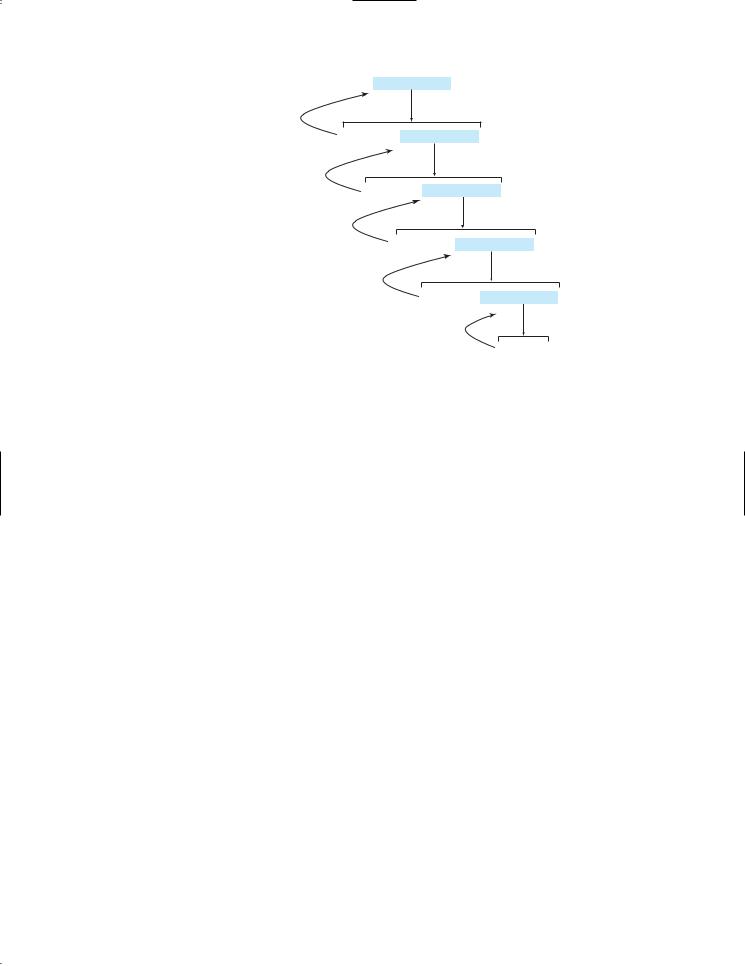
factorial(4)
Step 0: executes factorial(4)
Step 9: return 24
return 4 * factorial(3)
Step 1: executes factorial(3)
Step 8: return 6
return 3 * factorial(2)
Step 2: executes factorial(2)
Step 7: return 2
return 2 * factorial(1)
Step 3: executes factorial(1)
Step 6: return 1
return 1 * factorial(0)
Step 4: executes factorial(0)
Step 5: return 1
return 1
FIGURE 20.2 Invoking factorial(4) spawns recursive calls to factorial.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Space Required |
|
|
|
|
|
|
|
|
|
|
|
for factorial(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n: 0 |
|
|
|
|
|
|
|
|
4 |
Space Required |
|
Space Required |
|
|
|
|
|
|
|
|
|
for factorial(1) |
|
for factorial(1) |
|
|
|
|
|
|
|
|
|
n: 1 |
|
n: 1 |
|
|
|
|
|
3 |
Space Required |
|
|
Space Required |
|
Space Required |
|
|
|
|
|
|
for factorial(2) |
|
|
for factorial(2) |
|
for factorial(2) |
|
|
|
|
|
|
n: 2 |
|
|
n: 2 |
|
n: 2 |
|
|
|
|
|
|
Space Required |
|
|
Space Required |
|
|
|
|
|
2 |
Space Required |
|
|
|
|
Space Required |
||
|
|
|
|
for factorial(3) |
|
for factorial(3) |
|
|
for factorial(3) |
|
for factorial(3) |
|
|
|
|
n: 3 |
|
n: 3 |
|
|
n: 3 |
|
n: 3 |
|
1 |
Space Required |
|
Space Required |
|
Space Required |
|
|
Space Required |
|
Space Required |
|
|
for factorial(4) |
|
for factorial(4) |
|
for factorial(4) |
|
|
for factorial(4) |
|
for factorial(4) |
|
|
n: 4 |
|
n: 4 |
|
n: 4 |
|
|
n: 4 |
|
n: 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
Space Required |
|
|
|
|
|
|
|
|
|
|
|
for factorial(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n: 1 |
|
|
|
|
|
|
|
|
|
|
|
Space Required |
7 |
Space Required |
|
|
|
|
|
|
|
|
|
for factorial(2) |
|
for factorial(2) |
|
|
|
|
|
|
|
|
|
n: 2 |
|
n: 2 |
|
|
|
|
|
|
|
|
|
Space Required |
|
Space Required |
8 |
Space Required |
|
|
|
|
|
|
|
for factorial(3) |
|
for factorial(3) |
|
for factorial(3) |
|
|
|
|
|
|
|
n: 3 |
|
n: 3 |
|
n: 3 |
|
|
|
|
|
|
|
Space Required |
|
Space Required |
|
Space Required |
|
1 |
Space Required |
|
|
|
|
for factorial(4) |
|
for factorial(4) |
|
for factorial(4) |
|
|
for factorial(4) |
|
|
|
|
n: 4 |
|
n: 4 |
|
n: 4 |
|
|
n: 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FIGURE 20.3 When factorial(4) is being executed, the factorial method is called recursively, causing stack space to dynamically change.

20.3 Problem: Computing Fibonacci Numbers 681
 Pedagogical Note
Pedagogical Note
It is simpler and more efficient to implement the factorial method using a loop. However, we use the recursive factorial method here to demonstrate the concept of recursion. Later in this chapter, we will present some problems that are inherently recursive and are difficult to solve without using recursion.
20.3 Problem: Computing Fibonacci Numbers
The factorial method in the preceding section could easily be rewritten without using recursion. In some cases, however, using recursion enables you to give a natural, straightforward, simple solution to a program that would otherwise be difficult to solve. Consider the well-known Fibonacci-series problem:
The series: |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 ... |
indices: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
The Fibonacci series begins with 0 and 1, and each subsequent number is the sum of the preceding two. The series can be recursively defined as follows:
fib(0) = 0; fib(1) = 1;
fib(index) = fib(index - 2) + fib(index - 1); index >= 2
The Fibonacci series was named for Leonardo Fibonacci, a medieval mathematician, who originated it to model the growth of the rabbit population. It can be applied in numeric optimization and in various other areas.
How do you find fib(index) for a given index? It is easy to find fib(2), because you know fib(0) and fib(1). Assuming that you know fib(index - 2) and fib(index - 1), you can obtain fib(index) immediately. Thus, the problem of computing fib(index) is reduced to computing fib(index - 2) and fib(index - 1). When doing so, you apply the idea recursively until index is reduced to 0 or 1.
The base case is index = 0 or index = 1. If you call the method with index = 0 or index = 1, it immediately returns the result. If you call the method with index >= 2, it divides the problem into two subproblems for computing fib(index - 1) and fib(index - 2) using recursive calls. The recursive algorithm for computing fib(index) can be simply described as follows:
if (index == 0) return 0;
else if (index == 1) return 1;
else
return fib(index - 1) + fib(index - 2);
Listing 20.2 gives a complete program that prompts the user to enter an index and computes the Fibonacci number for the index.
LISTING 20.2 ComputeFibonacci.java
1 import java.util.Scanner;
2
3 public class ComputeFibonacci {
4/** Main method */
5 public static void main(String args[]) {
6// Create a Scanner
7Scanner input = new Scanner(System.in);
8 System.out.print("Enter an index for the Fibonacci number: ");
682 Chapter 20 |
Recursion |
|||||||
|
9 |
int index = input.nextInt(); |
||||||
|
10 |
|
|
|
|
|
|
|
|
11 |
// Find and display the Fibonacci number |
||||||
|
12 |
System.out.println( |
||||||
|
13 |
"Fibonacci number at index " + index + " is " + |
fib(index) |
); |
||||
|
14 |
} |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
16 |
/** The method for finding the Fibonacci number */ |
||||||
|
17 |
public static long |
fib(long index) |
{ |
|
|
||
base case |
18 |
if (index == 0) // Base case |
||||||
|
19 |
return 0; |
||||||
base case |
20 |
else if (index == 1) // Base case |
||||||
|
21 |
return 1; |
||||||
|
22 |
else // Reduction and recursive calls |
||||||
recursion |
23 |
return |
fib(index - 1) + fib(index - 2) |
; |
|
|
||
|
24 |
} |
|
|
|
|
|
|
|
25 |
} |
|
|
|
|
|
|
Enter an index for the Fibonacci number: 1
Fibonacci number at index 1 is 1
Enter an index for the Fibonacci number: 6
Fibonacci number at index 6 is 8
Enter an index for the Fibonacci number: 7
Fibonacci number at index 7 is 13
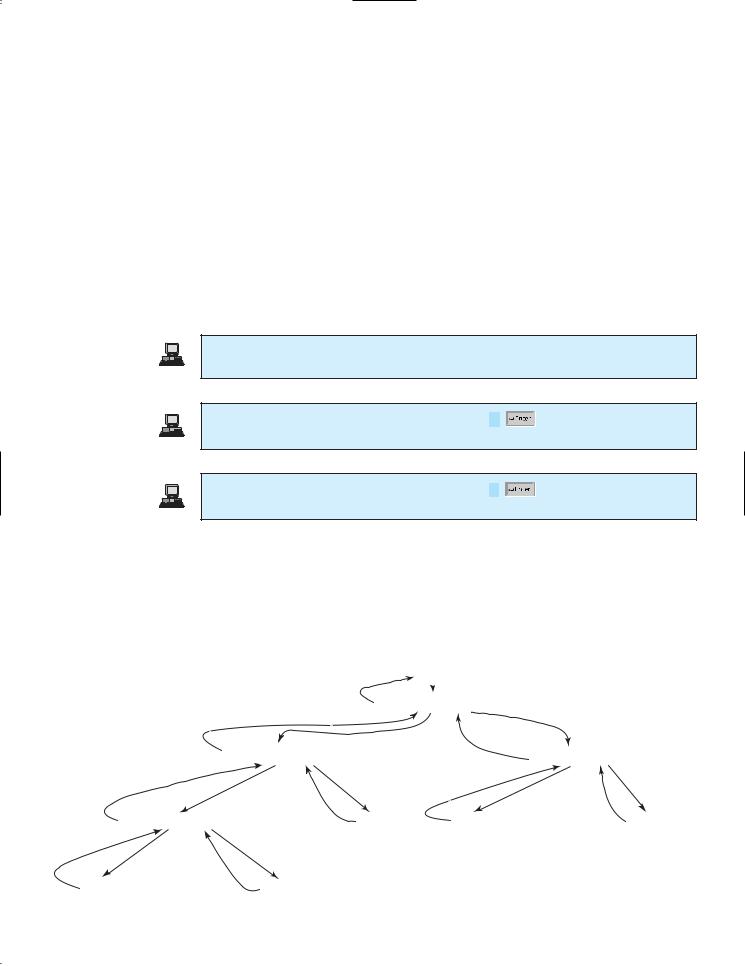
The program does not show the considerable amount of work done behind the scenes by the computer. Figure 20.4, however, shows successive recursive calls for evaluating fib(4). The original method, fib(4), makes two recursive calls, fib(3) and fib(2), and then returns fib(3) + fib(2). But in what order are these methods called? In Java, operands are evaluated from left to right. fib(2) is called after fib(3) is completely evaluated. The labels in Figure 20.4 show the order in which methods are called.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fib(4) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17: return fib(4) |
|
|
|
0: call fib(4) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
return |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fib(3) |
fib(2) |
11: call fib(2) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10: return fib(3) |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1: call fib(3) |
|
|
16: return fib(2) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
return |
fib(2) |
+ |
fib(1) |
|
|
|
|
|
|
|
|
|
|
|
|
return |
fib(1) |
+ |
fib(0) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
7: return fib(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
8: call fib(1) |
|
13: return fib(1) |
|
|
|
14: return fib(0) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12: call fib(1) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2: call fib(2) |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9: return fib(1) |
|
|
|
|
|
|
|
|
|
|
15: return fib(0) |
|
|
|||||||||
|
|
|
return |
fib(1) |
+ |
fib(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
return 1 |
|
|
|
|
|
return 1 |
|
|
|
|
return 0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4: return fib(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5: call fib(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3: call fib(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
6: return fib(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
return 1 |
|
|
|
|
return 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
FIGURE 20.4 Invoking fib(4) spawns recursive calls to fib.
