
- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
3. Двумерное стационарное движение газа. Уравнение Чаплыгина
Рассмотрим двумерные стационарные течения газа.
Ур неразрывности:
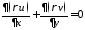
Ур движения:
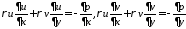
Система незамкнута,
поэтому добавим ур адиабатичности:

Если течение
осесимметричное
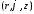 ,
то оно не зависит от
,
то оно не зависит от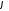 .
В этом случае
.
В этом случае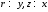
Ур неразрывности
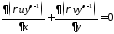 ,
если
,
если =1
–плоское,
=1
–плоское, =2
– осесимметричное.
=2
– осесимметричное.
Остальные уравнения остаются прежними.
Теперь введем функцию
тока
 :
: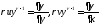
Движение удобно рассматривать в естественной системе координат.
Установим связь.

В дальнейшем будем
рассматривать
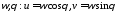
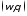 - плоскость годографа.
- плоскость годографа.
Возьмем
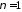 .
Тогда:
.
Тогда:
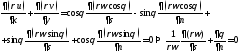
Уравнения движения:
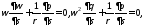
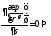 энтропия
постоянна вдоль линии тока. Система
замкнута, неизвестны
энтропия
постоянна вдоль линии тока. Система
замкнута, неизвестны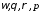
Чтобы получить уравнение
Чаплыгина, рассмотрим потенциальное
двумерное стационарное установившееся
течение. Вихри отсутсвуют,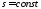
Вводим потенциал:
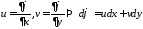 .
Введем функцию
.
Введем функцию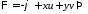
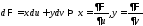 (1)
(1)
В дальнейшем будем
пользоваться ур неразрывности сжимаемой
среды
 .
.
Переходим от
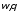 описанным ранее способом.
описанным ранее способом.
Найдем
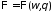 :
(1)
:
(1)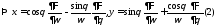
Подставляя (2) и выражения
для
 в
в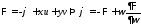
Чтобы получить ур,
определяющее
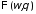 ,
используем:
,
используем: где
где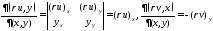 Домножим на
Домножим на и получим
и получим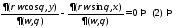
 Из
уравнения Эйлера вдоль линии тока
Из
уравнения Эйлера вдоль линии тока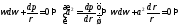
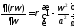 Подставив
последнее в (*) , получим уравнение
Чаплыгина:
Подставив
последнее в (*) , получим уравнение
Чаплыгина:
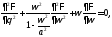
 В
общем случае решается методом разделения
переменных.
В
общем случае решается методом разделения
переменных.
Билет 43
1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
Опр.
М-ца размерности
![]() (
(![]() ,
,![]() )
– это таблица, которая заполнена числами
изR
(действ. числа)
или C
(комплекс.):
)
– это таблица, которая заполнена числами
изR
(действ. числа)
или C
(комплекс.):
 ,
,
![]() ,
,![]() .
.![]() - мн-во всех м-ц разм.
- мн-во всех м-ц разм.![]() на поле вещ. чисел.
на поле вещ. чисел.
М-цы размерности
![]() называются квадратными;
называются квадратными;![]() - вектор-строка;
- вектор-строка;![]() - вектор-столбец;
- вектор-столбец;![]() - нулевая м-ца (все эл-ты - нули);
- нулевая м-ца (все эл-ты - нули);![]() - единичная м-ца.
- единичная м-ца.
Операции над матрицами:
сложение:
![]() ,
,
![]()
![]()
Св-ва: коммутативно,
ассоциативно,
![]() является нулем для сложения,
является нулем для сложения,![]() м-ца
м-ца![]() обладает противоположной
обладает противоположной![]() ,
т.е.
,
т.е.![]() .
.
умножение:
производится по правилу «строка на столбец»:
![]() ,
,
![]() ,
,![]()

Част. случай:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Св-ва:
![]() (ассоц.);
(ассоц.);![]() ,
,![]() - размер.
- размер.![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() .
.
умножение на скаляр:
![]() ,
,
![]() ,
,![]()
![]()
Св-ва:
![]() ;
;![]() ;
;![]() ;
;![]() .
.
транспонирование:
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]()
Св-ва:
![]() ;
;![]() ;
;![]() .
.
![]() ,
,
![]() .
Определитель м-цыA
обозначается
.
Определитель м-цыA
обозначается
![]() ,
,![]() или
или![]() .
.
Пр-ры: n=1:
![]() - число;n=2:
- число;n=2:
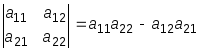 и т.д. Опр-ль м-цыA
= сумме своих членов. Член опр-ля
и т.д. Опр-ль м-цыA
= сумме своих членов. Член опр-ля
![]() -произв. эл-в м-цыA,
взятых по 1-му из кажд. стр. и кажд. столб.
со зн. + или -. Пусть из 1-й стр. в член
опр-ля взят эл-т
-произв. эл-в м-цыA,
взятых по 1-му из кажд. стр. и кажд. столб.
со зн. + или -. Пусть из 1-й стр. в член
опр-ля взят эл-т
![]() ,
из второй -
,
из второй -![]() и т.д. Из опр-я члена опр-ля
и т.д. Из опр-я члена опр-ля![]()
![]() - перест.
- перест.![]() .
И наоборот, кажд. перест.
.
И наоборот, кажд. перест.![]() дает член опр-ля.
дает член опр-ля.![]() ,
где
,
где![]() - кол-во инверсий в этой перест. И:Опр.
- кол-во инверсий в этой перест. И:Опр.
![]() .
.
Основные св-ва определителей: (все написанное ниже верно и для столбцов)
Th.
1 (вынес-е
общ. множ. из строки). Пусть B
получена из A
умножением всех эл-в какой-либо (одной)
строки на число
![]() ,
то
,
то![]() .
.
Д-во:
![]() /т.к.
/т.к.![]() ,
,![]() при
при![]() /
/![]()
![]() .
.
Th.
2 (расщепл.
по стр.). Пусть i-я
стр. м-цы A
имеет вид:
![]() ,
,![]() ,
...,
,
...,![]() .
Тогда
.
Тогда![]() ,
гдеB
получ. из A
зам-й ее i
стр. на стр.
,
гдеB
получ. из A
зам-й ее i
стр. на стр.
![]() ,
аC
– зам-й i
стр. на стр.
,
аC
– зам-й i
стр. на стр.
![]() .
(Верно и для случ. > 2-х слаг-х).
.
(Верно и для случ. > 2-х слаг-х).
Д-во:
![]() при
при![]() ,
,![]()
![]() /раскр.
скобки и груп./
/раскр.
скобки и груп./![]() .
.
Th.
3 Если в A
две строки пропорциональны, то
![]() .
.
Д-во: Пусть проп. i
и k
стр. м-цы A,
т.е.
![]() ,
,![]() .
Достат. д-ть, что
.
Достат. д-ть, что![]() ,
если вA
две =-е стр., т.к. по Th
«вынесение общего множит. за скобки»:
,
если вA
две =-е стр., т.к. по Th
«вынесение общего множит. за скобки»:
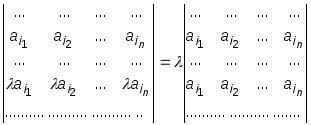 .
.
Идея док-ва:
![]()
![]() ,
(i<k).
Из усл. Th
,
(i<k).
Из усл. Th
![]() члены опр-ля расп-ся на пары взаим. обр-х
вида:
члены опр-ля расп-ся на пары взаим. обр-х
вида:![]()
![]() .
.
 ,
т.к.
,
т.к.
![]() ,
,![]() .
.
Th.
4 М-ца B
получ. из A
прим-м элем. пр-я (к i
стр. + k,
*-я на ч.
![]() ),
тогда
),
тогда![]() .
Д-во:
.
Д-во: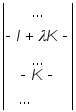 =/Th
«расщ-е по стр.»/=
=/Th
«расщ-е по стр.»/=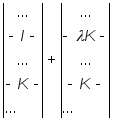 =/Пред.Th/
=
=/Пред.Th/
=![]() .
.
Th. 5 Опр-ль м-цы меняет знак при перест. 2-х строк.
Д-во:
 .
.
Th.
6 Опр-ль
трансп. м-цы = опр-лю исх. м-цы:
![]() .
(
.
(![]() ,
что все св-ва опр-й, полученные выше для
строк, справедливы и для столбцов).
,
что все св-ва опр-й, полученные выше для
строк, справедливы и для столбцов).
Th.
7 (произв.
квадрат. м-ц).
![]() ,
А и В – квадр. м-цы одного порядка.
,
А и В – квадр. м-цы одного порядка.
Д-во: По Th
4 и Лемме (![]() м-цыA
справ.: 1.
м-цыA
справ.: 1.
![]() - получ. изA,
если к i
стр.+ j
стр., умн-ю на
- получ. изA,
если к i
стр.+ j
стр., умн-ю на
![]() ;
2.
;
2.![]() - получ. изA,
если к j
столб. + i,
умнож-й на
- получ. изA,
если к j
столб. + i,
умнож-й на
![]() )
)![]()
![]() ,
гдеC
– произв. м-ца, P
– элемент.
,
гдеC
– произв. м-ца, P
– элемент.
![]()
![]() ,
,![]() и
и![]() - элем. ПоTh
(
- элем. ПоTh
(![]() кв. м-цаA
м.б. предст. в виде:
кв. м-цаA
м.б. предст. в виде:
![]() ,
,![]() ,
где
,
где![]() ,
,![]() - элем., а
- элем., а![]() и
и![]() - верх. тр. м-цы)
- верх. тр. м-цы)![]()
![]() ,
,![]()
![]()
![]() ,
,![]() и
и![]() .
Опр. в. тр. м-цы = *-ю диаг. эл-в
.
Опр. в. тр. м-цы = *-ю диаг. эл-в![]()
![]() ,
,![]() и
и![]()
![]()
![]()
![]()
![]() .
.
Опр.
![]() .
Обратная матрица к
.
Обратная матрица к![]() - такая
- такая![]() ,
что
,
что![]() .
.
Th.
(критерий обратимости). Обратная м-ца к
![]()
![]()
![]()
![]() .
При этом:
.
При этом:
 .
.
Опр.
Системой
![]() линейных ур-й с
линейных ур-й с![]() неизвестными наз-ся система вида:
неизвестными наз-ся система вида:
![]()
![]() (1)
(1)
.........................................
![]()
![]() - нек. числа (причем
- нек. числа (причем
![]() наз-ся коэф-ми, а
наз-ся коэф-ми, а![]() своб-ми чл-ми),
своб-ми чл-ми),![]() -
неизв.
-
неизв.
Рассм.
cист.
![]() лин-х ур-й с
лин-х ур-й с![]() неизвестными. Ее матрич. зап.:
неизвестными. Ее матрич. зап.:![]() ,
(2)
,
(2)
где:
 ,
,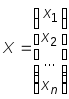 ,
,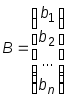 .
.
Th.
(правило Крамера). Если
![]() ,
то система (2) имеет единственное решение,
которое считается следующим образом:
,
то система (2) имеет единственное решение,
которое считается следующим образом:![]() ,
,![]() ,...,
,...,![]() ,
,
где
![]() - опр-ль м-цы
- опр-ль м-цы![]() ,
полученной из
,
полученной из![]() заменой
заменой![]() -го
столбца на столбец
-го
столбца на столбец![]() .
.
Д-во:
Т.к.
![]() ,
то
,
то![]()
![]() .
Получаем:
.
Получаем:![]() .
.
Достаточно
проверить, что
![]() имеет вид:
имеет вид: .
.
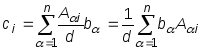 ,
,
![]() /разложение
по
/разложение
по
![]() -му
столбцу/
-му
столбцу/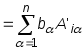 .
Осталось только заметить, что
.
Осталось только заметить, что![]() (т.е. алгебраич. дополнение к позиции
(т.е. алгебраич. дополнение к позиции![]() )
равно
)
равно![]() в м-це
в м-це![]() .
.
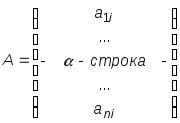 ,
,
 .
Отсюда
.
Отсюда![]() ,
что
,
что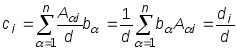 ,
т.е.
,
т.е.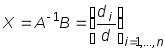
![]()
![]() .Th
док-на.
.Th
док-на.
